包含密集模态的空间结构的模糊主动振动控制*

刘潇翔，胡 军

(1.北京控制工程研究所,北京100190; 2.空间智能控制技术国家级重点实验室,北京 100190)

包含密集模态的空间结构的模糊主动振动控制*

刘潇翔1,2，胡 军1,2

(1.北京控制工程研究所,北京100190; 2.空间智能控制技术国家级重点实验室,北京 100190)

分析和总结了典型密频系统特性及其对控制的影响.针对密频系统的模态不稳定特性及密集模态的低可控度问题，引入一定数量的压电类智能结构作为传感器和作动器，基于独立模态空间设计了针对结构包含密集模态的参数自调整模糊主动振动控制系统.该系统对密频系统的不确定性和溢出干扰项具有鲁棒性，且能充分利用作动器的作动能力，在作动能力有限的前提下，相比于传统控制方法可更为有效地抑制结构振动.最后以典型密频系统在轨工作时受到的两种主要激励模式为例，仿真证实了该方案的正确性和有效性.

空间结构; 密集模态; 模态不稳定; 模糊振动控制

大跨度、复杂化航天结构的许多构件及设备具有大挠度、弱阻尼、低频段模态密集等结构弱势，加之高精度、高稳定度性能指标的提出，使得被动振动抑制难以满足要求，因此主动振动控制日益得到重视.

对轻阻尼模态密集结构的控制一直是主动振动控制的难点[1-3]，结构低阶控制的关键是在欠配置条件下得到满意的控制效果.然而，首先密频系统的模态不稳定特性意味着控制对象存在严重不确定性，即被控对象结构参数有微量摄动时，其模态参数(尤指振型)可能在很大范围内变化[4]，控制系统设计必须充分考虑不确定性的影响[5].独立模态控制(IMSC，independent modal space control)是目前结构低阶控制中的常用方法，而IMSC中物理坐标与模态坐标间的转换需要用到被控对象的振型信息[6]，故而这种不确定性的影响很大.其次，密集模态之间的强相关性将加剧控制溢出和观测溢出.基于剩余模态作用机理可将溢出问题等效为干扰项[7]，如果控制方法对干扰项鲁棒性不强，则会严重降低控制系统性能.传统控制方法要求被控对象精确的数学模型，而模糊控制则适用于模型具有不确定性的被控对象，且通过参数自调整可实现较好的抗干扰性.最后，针对密集模态的低可控度问题[3,8]，模糊控制的非线性特性可最大限度利用作动器作动能力，用尽量少的能源在尽可能短的时间内达到振动抑制的目的.

因此，本文基于独立模态空间设计了针对结构包含密集模态的参数自调整模糊主动振动控制系统，参数调整及控制规则简单易实现，容易满足实时性要求，抗干扰性能良好，且相比于传统模糊控制方法，响应过程的控制量分配更合理.

1 问题模型

1.1模型数学描述

挠性结构本身是无限自由度分布参数系统，经有限元法离散化，可表示为二阶常微分方程组.设离散化后系统整体自由度为n，则系统模型为

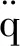
式中，M为质量阵，C为阻尼阵，K为刚度阵，q(t)为位移矢量，B为控制输入阵，u(t)为控制力矢量，Cr,Cd为输出矩阵，y(t)为量测向量.满足

ΦTMΦ=I,

的转移矩阵Φ可将式(1)转化为模态坐标表达式.这里设阻尼为瑞利阻尼，即满足C=αM+βK，α，β为常数，则Φ也可将C对角化

ΦTCΦ=diag{2ξ1ω1,…,2ξnωn},

令q(t)=Φη(t)，则式(1)和(2)的模态坐标表达式为

其中，

D=diag{2ξ1ω1,…,2ξnωn}，

低阶IMSC设计中，取被控模态数为m，Φc为系统前m阶模态组成的n×m维矩阵，用Φc代替Φ，则近似有q(t)=Φcηc(t)，ηc(t)∈Rm×1为前m阶主模态坐标.式(3)、(4)改写成

其中，

Dc=diag{2ξ1ω1,…,2ξmωm}，

1.2密频系统特性及其对控制的影响

(1) 模态不稳定特性

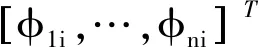
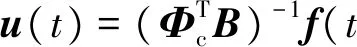
此外，配置传感器时考虑使矩阵CdΦc及CrΦc非奇异，则通过

ηc(t)=(CdΦc)-1yd(t),

可观测模态坐标.

可见，模态控制力转化为实际控制力及模态坐标获取过程都用到模态信息Φc，密频系统的振型不稳定特性将严重影响模态控制性能.

(2) 溢出问题

定理1.结构低阶控制中的剩余模态的作用效果可等价为控制方程的干扰，干扰模型[7]为

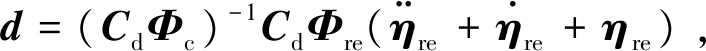
对于包含密集模态的结构来讲，在密频组欠配置情况下，剩余模态中包含密频组内模态，密集模态之间相互影响强烈，控制输出对未控密集模态影响大，同样未控密集模态对振动输出贡献也大.如果控制方法对干扰的鲁棒性不强，将加剧溢出问题，严重影响振动抑制性能，甚至造成不稳定.

(3) 低可控/可观度

密集模态组内各模态可控/可观度存在相互影响[8-9]，在密频组欠配置(控制量/观测量维度小于密集模态数)的条件下，即使按照文献[9]的方法合理分配可控/可观度，系统对控制量的要求仍然很高，而主动振动控制中广泛应用的压电智能元件的作动能力有限，如何合理利用有限的作动能力，在短时间内抑制振动是密频系统对控制提出的实际需求.

2 密频系统的参数自调整模糊振动控制设计

传统控制方法适用于模型已知或可辨识的对象，而密频系统的模态不稳定特性意味着控制对象存在严重不确定性，尤其当控制过程利用到被控对象振型信息(如IMSC)时，这种不确定性的影响更大，而模糊控制不需要准确地控制对象模型，适用于这类被控对象.

2.1典型密频结构

具有模态局部化现象的系统是典型的密频结构，参照文献[10]中Daisy模拟仿真器肋条锥外振动(见图1)，构造10自由度模型，各阶频率和振型分别如表1和图2(a)所示，最大阻尼比ζi<2%.依文献[4]中模态密集程度界定方法，可知前5阶模态是高度密集模态组，与直观判断一致.结构参数微量摄动(Δk8,8=0.0001≪k8,8=5966.5)时，密集模态振型就有很大变化(如图2(b))，表现出典型的模态不稳定特性.

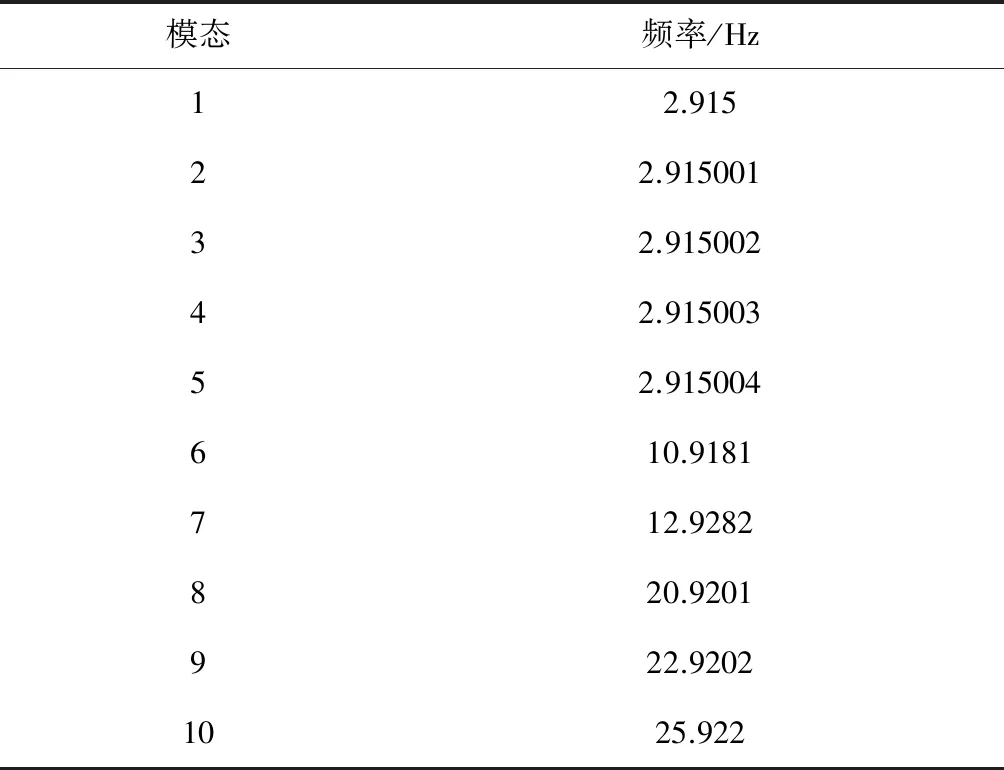
表1 模型各阶频率

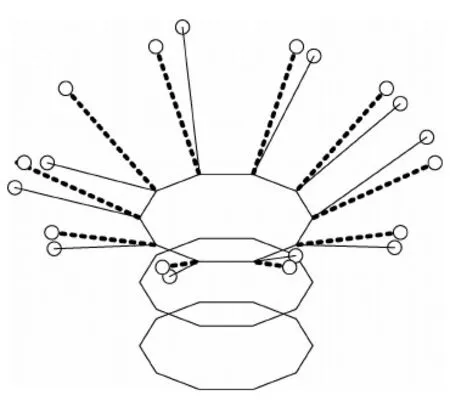
图1 肋条锥外振动示意图

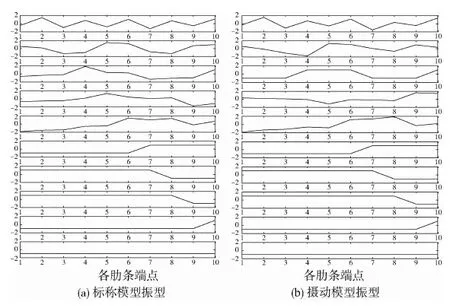
图2 模型振型

2.2参数自调整模糊振动控制

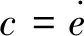
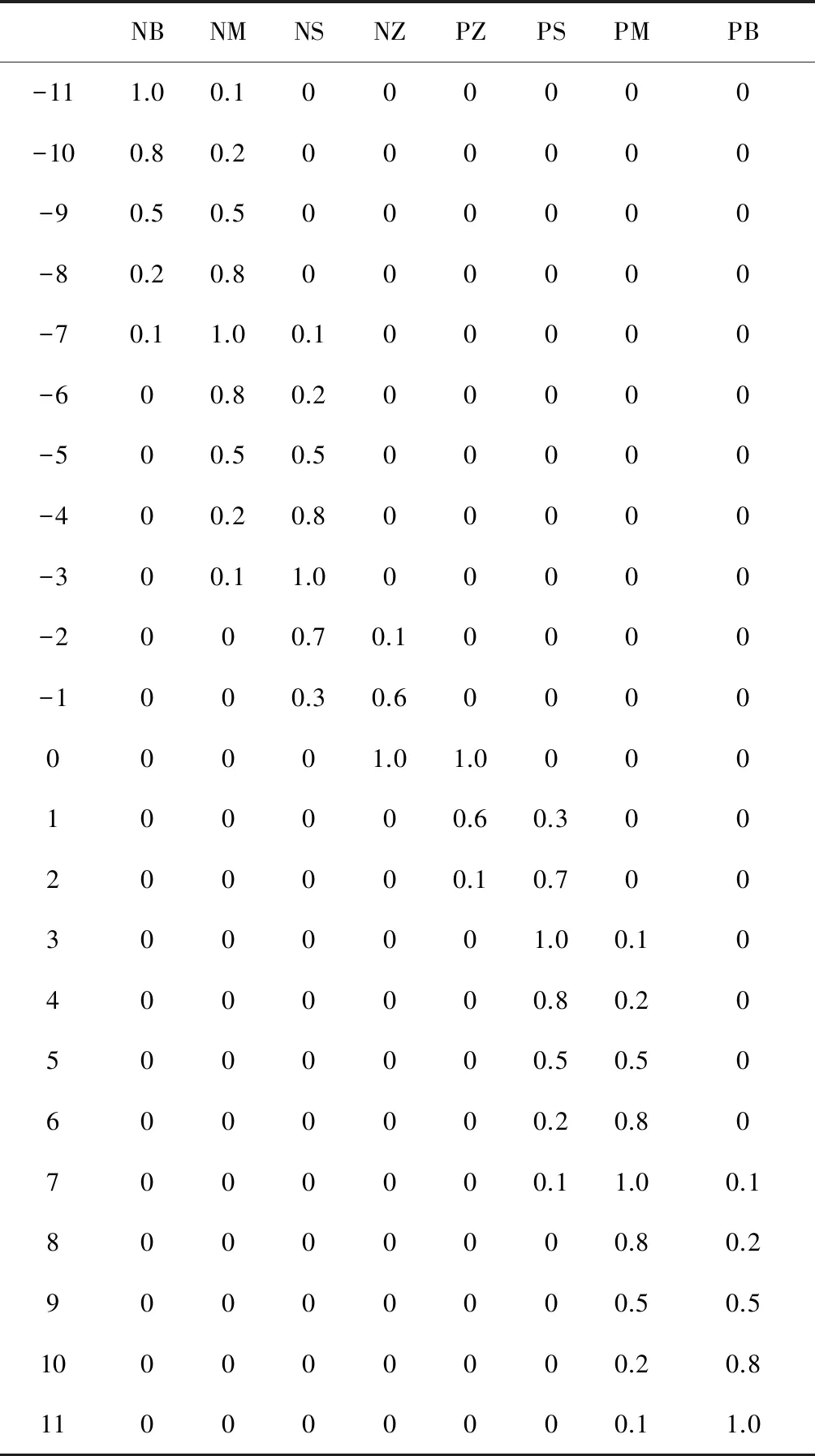
表2 输入误差的隶属度

模糊控制器的性能除了取决于模糊控制规则外，输入变量的量化因子Ke、Kc和输出控制量的比例因子Kf等参数也起着至关重要的作用.实验表明量化因子和比例因子的大小及不同量化因子之间大小的相对关系，对模糊控制器的性能影响极大[11].有时采用一组固定参数难以得到理想效果，通过在控制过程中调整参数可修改不同阶段的控制特性，从而达到良好的控制效果.

为此，这里参数Ke、Kc、Kf随e和c的变化而自调整：当e和c较大时进行粗控，缩小Ke、Kc，降低对e或c的分辨率，同时采取较大的控制量，放大Kf；而当e和c较小时，系统接近稳态，进行细控，放大Ke、Kc，提高对e或c的分辨率，同时采取慎微的控制量，缩小Kf.这一过程通过参数调整表中的参数调整倍数n来实现，取Ke′=n×Ke、Kc′=n×Kc、Kf′=Kf/n作为新参数进行运算.n的论域设为(1/8,1/4,1/2,1,2,4,8)，语言变量N取为AB(高放)，AM(中放)，AS(低放)，OK(不变)，CS(小缩)，CM(中缩)，CB(大缩)[11].调整倍数的隶属度见表5[11].参数自调整规则如表6所示[11].整个参数自调整模糊控制器结构如图3所示.

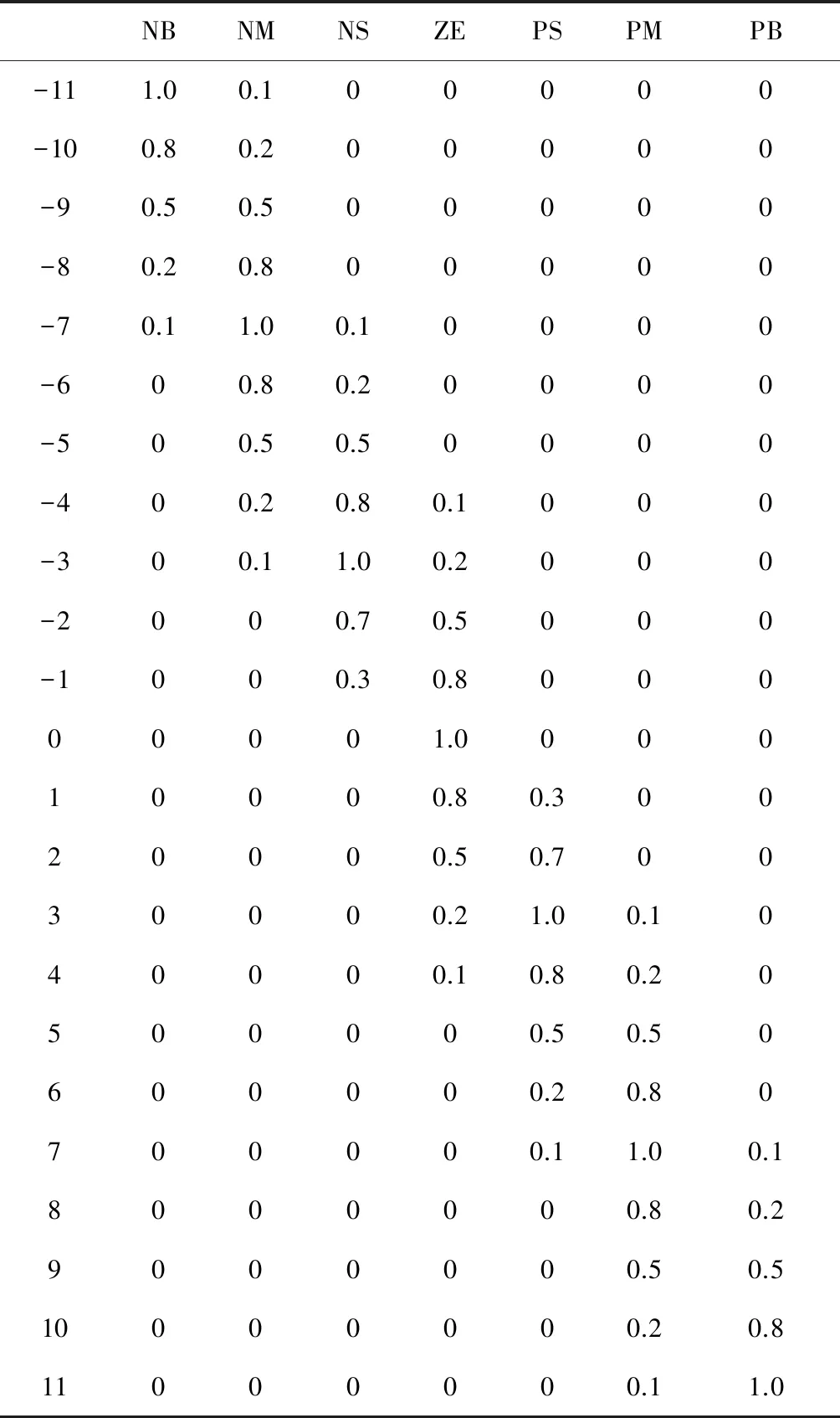
表3 输入误差变化和输出控制量的隶属度

图3 参数自调整模糊控制器

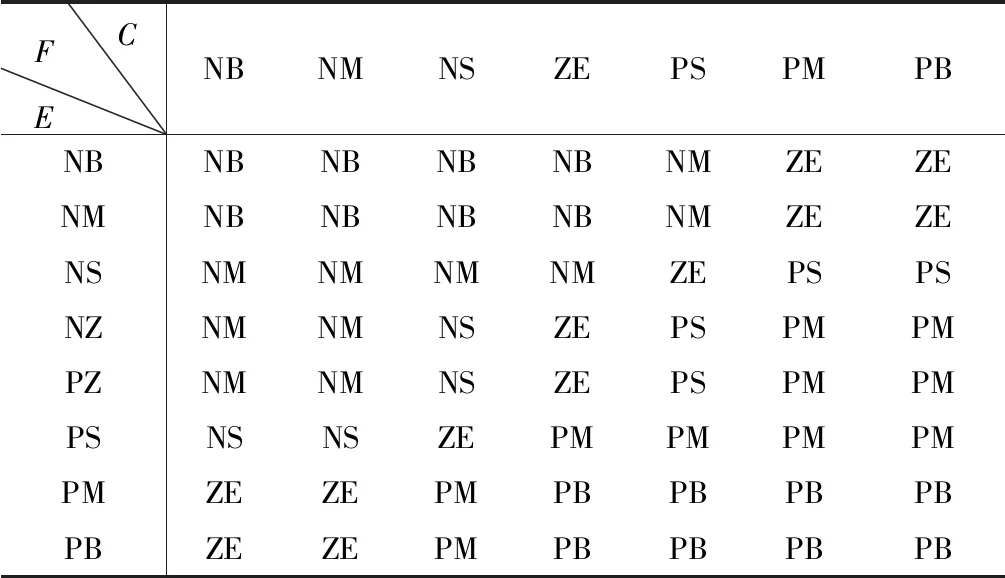
表4 模糊控制规则表

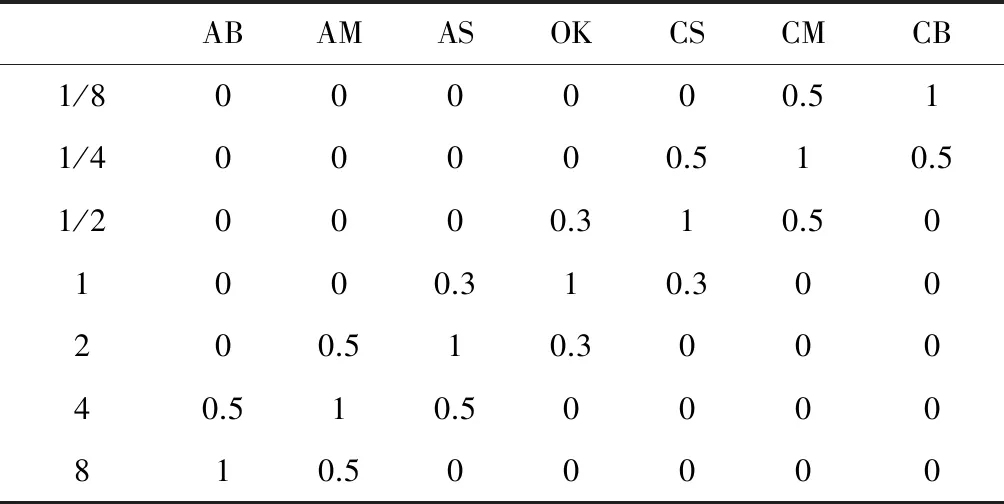
表5 参数调整倍数的隶属度

表6 参数调整规则表

3 仿真结果分析

对本例包含5阶密集模态的结构模型，选择4对传感器/作动器，该欠配置方式会造成密集模态的可控/可观度严重下降.根据文献[9]的方法配置元件位置，使密频组各阶模态整体可控度最优，采用同位配置，得到各对传感器/作动器位置为第6，8，9，10根肋条端点.由于结构包含5阶密集模态，而取前4阶模态作为主控模态，即剩余模态中包含密频组内模态，依定理1，剩余模态作用可等效为干扰，将给控制器性能带来严峻考验.考察模型在各模态位移及速度都相等的初始状态下的响应情况.基于独立模态空间：采用最优控制，受压电作动器作动能力限制，状态量权重Qi相对于控制量权重Ri不能取得太大，结合对控制量进行限幅，各观测点响应及各作动器输出控制量分别如图4～5所示；应用本文的参数自调整模糊控制系统，控制结果及控制量分别如图6～7所示.

显然，参数自调整模糊控制系统在该初始状态下可有效抑制振动，结果显示在5s后控制器输出接近零，振动幅值衰减95%以上.而在同样作动能力限制下，最优控制在优化目标函数中需要加大控制量的权重，使控制量输出在可作动范围系统振动衰减很慢.此外，模糊控制属非线性控制，对作动器输出利用更为充分，相比之下运用更少的能源，在更短的时间内使系统振动得到了有效抑制.

当Δk8,8=0.0001≪k8,8=5966.5时，摄动模型在同样初始条件下，仍采用上述两种控制系统，得到的控制效果分别如图8～10所示.可见，参数自调整模糊控制系统对表现出模态不稳定特性的摄动模型同样可以有效地进行振动抑制.而最优控制下摄动模型的第1阶模态出现了差拍现象(如图8所示)，是引发系统不稳定的隐患.

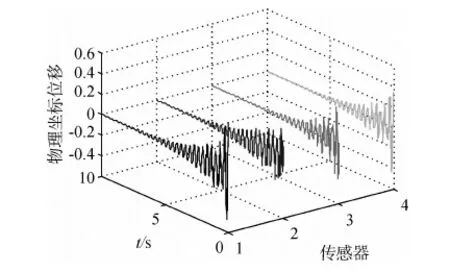
图4 最优控制结构响应

图5 最优控制量

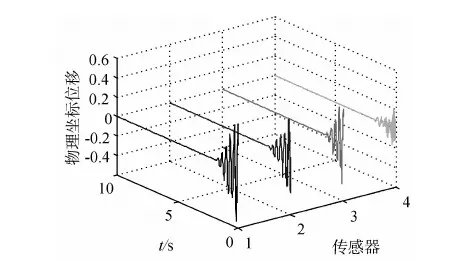
图6 参数自调整模糊控制结构响应

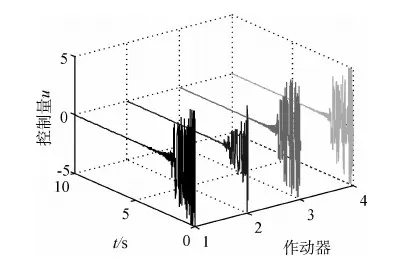
图7 参数自调整模糊控制量

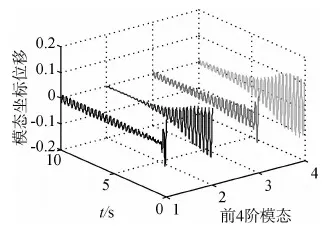
图8 摄动下的最优控制模态响应

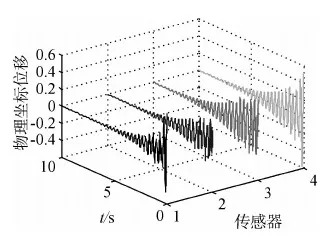
图9 摄动下的最优控制结构响应

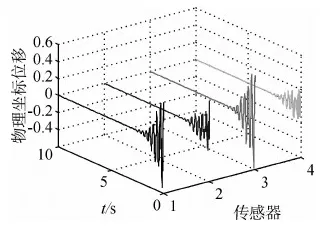
图10 摄动下的模糊控制结构响应

在自由度9处施加1.1倍基频(充分激起密频组振动)的正弦激励.简单模糊控制作用下各观测点受控响应及控制器输出曲线分别如图11～12所示；参数自调整模糊控制结果及控制量分别如图13～14所示.可见，参数自调整模糊控制系统的抗干扰性能较好，相比于简单模糊控制，在小幅提高振动衰减速度的基础上，其控制量输出可大幅减少.

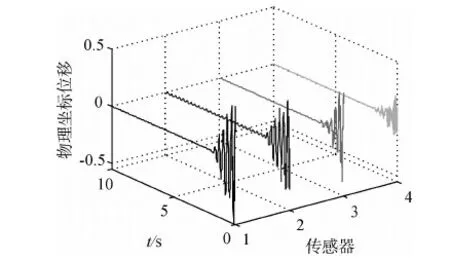
图11 简单模糊控制下的周期激励响应

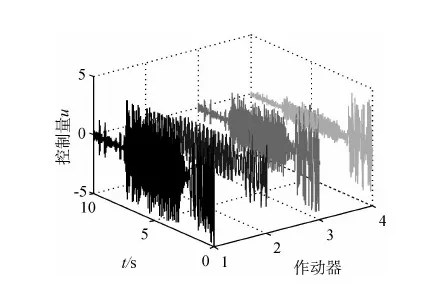
图12 简单模糊控制器输出

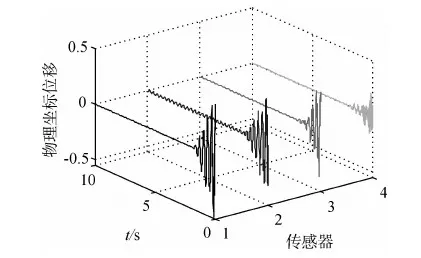
图13 参数自调整模糊控制下的周期激励响应

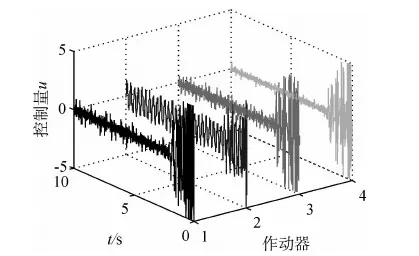
图14 参数自调整模糊控制器输出

值得一提的是，由于密频组内共5阶密集模态，而传感器/作动器仅4对，IMSC中主控模态为4阶，即未控动态中包含密频组内模态，从而加剧溢出问题.因剩余模态作用可等效为干扰，两种激励模式下振动均能得到有效抑制，所以进一步证实了该参数自调整模糊控制系统的抗干扰能力.

5 结 论

本文列举的密频系统特性及其对控制的影响，为大型空间结构主动振动控制设计提供了有益参考.针对包含密集模态结构所设计的参数自调整模糊振动控制系统，能克服密频系统模态不稳定特性和未建模动态的影响，并能充分利用作动器作动能力，在密集模态的低可控度和压电元件作动能力有限的前提下，相比传统控制方法和简单模糊控制取得了更优的控制效果，有着良好的应用前景.

[1] Abe M.Vibration control of structures with closely spaced natural frequencies by a single actuator[J].Journal of Vibration and Acoustics,1998,120(1):117-124

[2] Xu K,Warnitchai P,Igusa T.Active control of a structure with two closely spaced natural frequencies[R].AIAA-92-2216-CP: 1285-1295

[3] 刘一武,张洪华,吴宏鑫.可控性差的空间密集模态结构的振幅最优控制[J].自动化学报,2002,28(2): 1-6

[4] 刘潇翔,胡军.一种界定模态密集程度的新方法[J].宇航学报,2010,31(4): 1093-1099

[5] Ferrara A,Giacomini L.Control of a class of mechanical systems with uncertainties via a constructive adaptive/second order VSC approach[J].Journal of Dynamic Systems Measurement and Control,2000,122(1): 33-39

[6] Lindberg R E,Longman R W.On the number and placement of actuators for independent modal space control[C].AIAA/AAS Astrodynamics Conference,San Diego,California,August 9-11,1982

[7] 李东旭.大型挠性空间桁架结构动力学分析与模糊振动控制[M].北京: 科学出版社,2008

[8] Williams T,Cheng X.Degrees of controllability and observability for close modes of flexible space structures[J].IEEE Trans.Autom.Control,1999,44(9): 1791-1795

[9] Liu X X,Hu J.On the placement of actuators and sensors for flexible structures with closely spaced modes.[J].Sci China Tech.Sci,2010,53(7):1973-1982

[10] Zee R E,Hughes P C.Mode localization in flexible space craft: a control challenge[J].J.Guid.Control Dyn.,2000,23(1): 69-76

[11] 刘曙光,魏俊民,竺志超.模糊控制技术[M].北京: 中国纺织出版社,2001,6

FuzzyVibrationControlofSpaceStructureswithCloseModes

LIU Xiaoxiang1,2,HU Jun1,2

(1.BeijingInstituteofControlEngineering,Beijing100190，China;2.NationalKeyLaboratoryofScienceandTechnologyonSpaceIntelligentControl,Beijing100190，China)

For a space structure with closely spaced modes,the particularities and the corresponding impacts on control design are analyzed in this paper.Considering mode shape instability and low controllability/observability of close modes,and adopting piezoelectric elements as actuators and sensors,a self-adjusting fuzzy active vibration control system based on independent mode space is designed,which is robust to system uncertainties and the spillover disturbance of the structure with close modes.This control scheme can take full advantage of the control energy.When the actuator output is set to a limitation,a much more desirable vibration suppression is achieved by this scheme in comparison with traditional control approaches.Finally,the validity and effectiveness of the novel control scheme are verified on a model structure with close modes.

space structures; close modes; mode shape instability; fuzzy vibration control

V214; TB123; O32

A

1674-1579(2010)04-0018-07

*国家自然科学基金(10872028)资助项目.

2010-05-21

刘潇翔(1983—),女，吉林人，博士研究生，研究方向为航天器控制 (e-mail: monkeyfiona@163.com).