基于保险投资风险模型的破产分析

万冬梅，洪 岩

（1.商丘职业技术学院，河南 商丘 476000；2.华北水利水电学院，河南 郑州 450003）

0 引言

在保险精算中， 经典的风险模型及其推广模型对描述、刻画单一风险经营具有重要的作用。经典风险模型的索赔过程由poisson 过程构成，并且保费是固定不变的。 然而，在工作中，可变保费情形更加真实。随着风险经营的规模扩大，不同的顾客群将要求不同的保险合同， 保险公司会不断面临推出新险种的压力。 考虑到经典模型在刻画险种多样性上的局限性，提出一类双险种的风险模型，其索赔过程由复合poisson 与Cox 过程共同构成。 此前，已有很多作者将Cox 过程理论应用于风险论中[1～4]。

1 双险种风险模型

1.1 条件假设

（1）假设其中一个险种保费到达过程{M1(t);t≥0}是强度为λ1的泊松过程，且M1(0)=0，每次保费收入为常数c；另一险种保费到达过程{M2(t);t≥0}是强度为λ2的泊松过程，且M2(0)=0，但每次收到的保险费不再为常数研究，而是一系列相互独立的随机变量，记为{Yi}1∞，其分布函数为F1(x)，且二阶矩存在。

（2）假设一个险种理赔过程{N1(t);t≥0}是强度为μ1的泊松过程,N1(0)=0，理赔额是相互独立的随机变量，记为{Xi(1)}1∞，分布函数为F2(x)，且二阶矩存在；另一险种理赔过程{N2(t);t≥0} 是强度为μ2的泊松过程，N2(0)=0，理赔额是相互独立的随机变量，记为{Xi(2)}1∞，分布函数为F3(x)，且二阶矩存在。

（3） 设以上所涉及的4 个泊松过程和3 个随机变量序列是相互独立的，并且设始准备金为μ。

1.2 建立模型

在3 个假定条件约束下，盈余过程{U1(t);t≥0}为：

过程{S1(t)t≥0}表示保险公司在时刻t 的盈余部分。

设T=inf{t:t＞0 且U（t）＜0}表示保险公司破产发生的时刻（当T=∞时，因为对任意t＞0 均有U（t）＜0，即保险公司破产不会发生）。这里没有考虑保险业务涉及的除了保费和理赔以外的其他影响盈余资本因素，如附加费和保单所有人的分红等问题。

由以上分析得出保险公司的最终破产概率为：

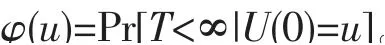
2 估计破产概率

用类似经典风险理论的方法推导出这一风险模型下最终破产概率的一般表达方式和Luindberg 不等式。

2.1 一般表达式的推导

双险种风险模型的一般表达式为： 对于盈余过程{S(t)；t≥0}，存在函数g(r)，使得：E[e-rS(t)]=etg(r)，并且g(r)=λ1(e-rc-1)+λ2[MY(-r)-1]+μ1[MX1(r)-1]+μ2[MX2(r)-1]。

该式的证明过程为：

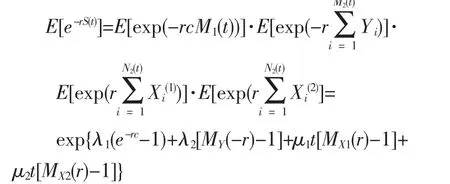
其中：MY=(-r)=E(e-rY),MX1(r)=E(e-rX(1))，MX2(r)=E(e-rX(2)).

令：g(r)=λ1(e-rc-1)+λ2[MY(-r)-1]+μ1[MX1(r)-1]+μ2[MX2(r)-1]。

得：E[e-rS(t)]=etan(r)。

2.2 不等式的推导

对于风险模型{U(t);t≥0}，最终破产概率为：

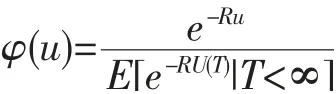
（R 为调节系数，是方程g(r)=0 当r＞0 时的唯一正解）。

该式的证明过程为：对于任意的t＞0，r＞0，有

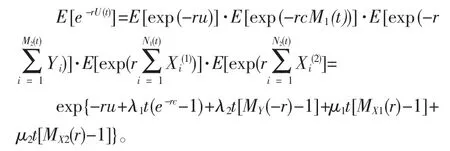
当R=g 时，g(R)=0,故E[e-Ru(x)]=e-Ru，将其代入(1)得：

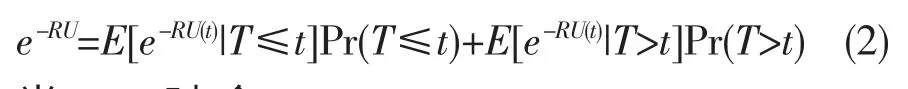
当T≤t 时,令U(t)=U(T)+[U(t)-U(T)]=

因为E[e-RU(t)｜T≤t]Pr(T≤t)=E[e-RU(t)｜T≤t｜]Pr(T≤t).

当t→∞时，limE[e-RU(t)｜T≤t｜]Pr(T≤t)=E[e-RU(t)｜T＜∞｜]Pr(T＜∞).

下证当t→∞时，式(2)右端第二项为零。

因为：E[U(t)]=u+(cλ1+λ2p1-μ1p1(1)-μ2p1(2))·t

Var[U(t)]=u+(c2λ1+λ2p2-μ1p2(1)-μ2p2(2))·t

记α=cλ1+λ2p1-μ1p1(1)-μ2p1(2)，β2=c2λ1+λ2p2-μ1p2(1)-μ2p2(2).

考虑，q(t)=u+αt-βt，因α＞0，在t 充分大时，q(t)=u+αt-βt＞0。

因此，E[e-RU(t)｜T＞t｜]=

E[e-RU(t)｜T＞t,0≤U(t)≤q(t)]Pr[0≤U(t)≤q(t)]+

E[e-RU(t)｜T＞t,U(t)＞q(t)]Pr[U(t)＞q(t)]≤

Pr[0≤U(t)≤q(t)]+exp[-Rq(t)].

由契比雪夫不等式得：0≤Pr[0≤U(t)≤q(t)]≤

当t→∞时，0≤E[e-RU(t)｜T＞t]≤t +exp[-Rq(t)]→0.

所以，e-Ru=φ(u).E[e-RU(t)｜t＞∞],

3 结语

在双险种的条件约束下，根据给定的初始状态，求出了满足破产概率的方程。根据建立的风险模型，推导出了破产概率的两种表达式。在风险控制中，破产概率表达式用于风险定量分析， 可以起到有效防控风险的作用。

[1] 蒋志明，王汉兴. 一类多险种风险过程的破产概率[J]. 应用数学与计算数学学报，2000（01）：9-16.

[2] 黄晓钟， 彭勤文. 一类多险种的风险模型及其破产概率[J]. 宁夏大学学报，2005（04）：306-310.

[3] 钟朝阳. 一推广后的双险种风险模型的破产问题[J]. 科技信息，2009（08）：367-369.

[4] 徐怀. 保费收入是复合泊松过程风险模型的破产概率[M]. 合肥工业大学，2004.