黄河下游游荡河型与弯曲河型之间的关系研究

彭 明，郭旭东，史传文

（黄河水利职业技术学院，河南 开封 475004）

0 引言

在我国， 通常按平面形态把冲积河流分为顺直、弯曲、分汊和游荡4 种基本河型[1]。 黄河下游普遍认可的河型分类为弯曲、游荡和过渡3 种，但是过渡河型不属于4 种基本河型范畴。 史传文等[2]根据冲积河流河型成因的输沙平衡程度理论假说，通过模糊聚类计算后认为，黄河下游仅存在弯曲和游荡2 种基本河型。 但弯曲和游荡两种河型之间的具体关系还不是特别清楚。 本文将根据冲淤标准化输沙平衡数的数据，采用集合数学方法，研究弯曲河型和游荡河型之间的集合关系。

1 黄河下游的河型分类

1.1 分为弯曲、游荡和过渡3 种河型

如前所述，黄河下游被普遍认可的河型分类为弯曲、游荡和过渡3 种河型，如表1 和图1 所示。

表1 普遍认可的黄河下游河型的分类Table 1 Universal approved river classification of lower Yellow River

图1 黄河下游河型分类示意图Fig.1 River classification of lower Yellow River

1.2 分为弯曲和游荡2 种河型

史传文等[2]认为，黄河下游仅存在弯曲和游荡2种基本河型。 具体分类如表2 所示。

表2 黄河下游两种河型分类结果Table 2 Two river classification results of lower Yellow River

2 黄河下游冲淤标准化输沙平衡程度数计算统计及其集合的个数

2.1 黄河下游冲淤标准化输沙平衡程度数计算及统计结果

冲积河流输沙平衡程度公式为

式中： W'ij为ΔLi河段、 Δtj时段的冲积河流输沙平衡程度数，是无量纲量；Qij、Sij、ωij、hij、Bij、Jij和nij分别为ΔLi河段Δtj时段的流量、含沙量、沉速、水深、河宽、比降和糙率的平均值。 为了保证Wij为无量纲量，式中单位只能用“kg、m、s”。

利用小浪底水库运用前11 年的水文年鉴资料[3]，把6 河段的11 年月均数据Qij、Sij、ωij、hij、Bij、Jij和nij输入式（1），计算得到6 个河段11 年的月均输沙平衡程度数W'ij各为132 组。 为了同量级地反映冲刷和淤积对河型的影响， 求出小于1.0 输沙平衡程度数的倒数，并与原来W'ij≥1.0 的数一起组成所谓的冲淤标准化输沙平衡程度数Wij。 各河段各组冲淤标准化输沙平衡数出现频率（%）见表3。

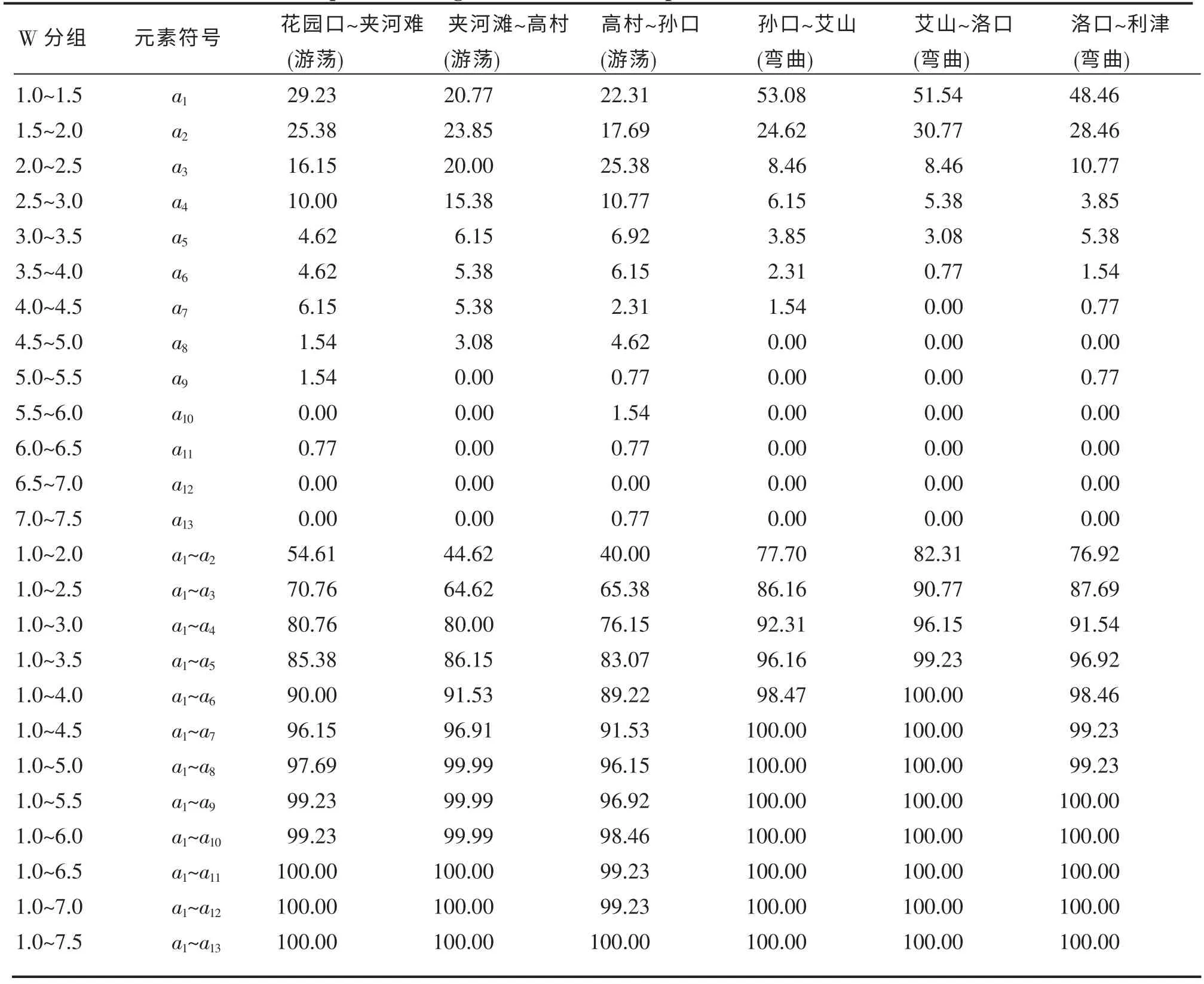
表3 黄河下游6 河段各组冲淤标准化输沙平衡程度数出现频率统计表 单位：%Table 3 Alluvial standardized equilibrium degree of sediment transport of six river sections of lower Yellow River (Unit: %)

2.2 冲淤标准化输沙平衡程度数集合的幂集个数

根据表3，黄河下游游荡和弯曲河型的冲淤标准化输沙平衡程度数W 的集合可以表述为

把A 的幂集记作P (A)。 若集合A 中的元素个数｜A｜=n，则A 的m(0≤m≤n) 的元子集有Cmn个，幂集P(A)的个数为

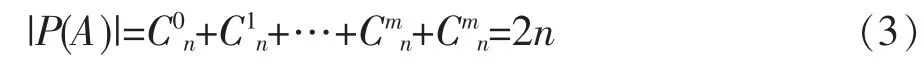
其中

计算得到的集合A 的m 元子集个数和幂集个数见表4。 把W 分为13 组，除去空集合外，如果1个子集都可以形成一种河型，就意味着可以形成8 191种河型。

表4 集合A 的m 元子集个数和幂集个数Table 4 Number of subset and power set of m variable of set A

3 两种河型的冲淤标准化输沙平衡程度数集合分析

3.1 游荡河型的冲淤标准化输沙平衡程度数集合

根据表4，可以得出，游荡河型的冲淤标准化输沙平衡程度数集合为

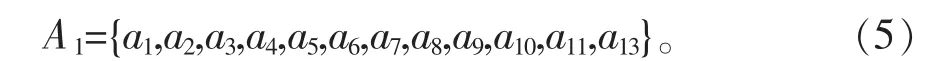
3.2 弯曲河型的冲淤标准化输沙平衡程度数集合

弯曲河型的冲淤标准化输沙平衡程度数集合为

3.3 两种河型的冲淤标准化输沙平衡程度数集合关系

集合A1与A2存在如下关系：

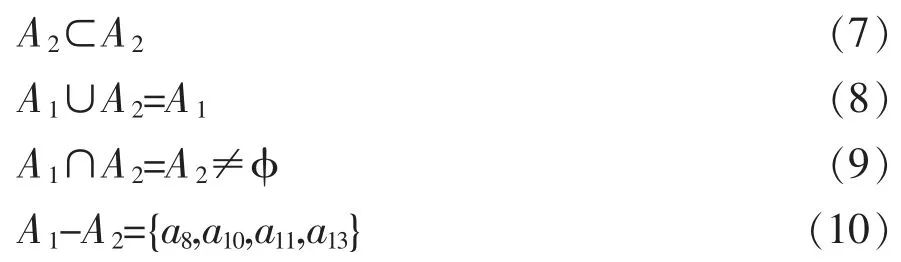
这说明，在冲淤标准化输沙平衡程度数方面，弯曲河型是游荡河型的真子集， 游荡河型包含弯曲河型，弯曲河型与游荡河型的重叠部分为弯曲河型，游荡河型比弯曲河型多些数值较大的冲淤标准化输沙平衡程度数。

4 结论

（1）游荡河型与弯曲河型比较，弯曲河型缺失较大的冲淤标准化稳定程度数， 较小的冲淤标准化稳定程度数在游荡河型中的重复度远远低于弯曲河型。 （2） 游荡河型与弯曲河型之间的关系为包容关系。

[1] 罗全胜， 史传文. 冲积河流河床综合稳定性指标研究[J].人民黄河2006（8）：19-20.

[2] 史传文，吴保生，马吉明. 冲积河流河型的成因及分类与判别计算方法研究[J]. 水力发电学报2007，26（5）：107-111.

[3] 黄河水利委员会. 中华人民共和国水文年鉴:黄河流域水文资料5 册 [M]. 郑州： 黄河水利出版社，1972，1973，1975，1976，1978，1979，1980，1982，1985，1987，1988.