基于保护平面热源法的防隔热材料热物性测量

王 强，戴景民，COPPA P

(1. 哈尔滨工业大学自动检测与过程控制系统研究所，哈尔滨 150001；2. 罗马大学机械工程学院，Rome 00133)

防隔热材料是航天器热防护系统中的重要部件，其隔热性能的优劣将直接关系到整个热防护系统的性能，是保障航天器稳定、安全运行的关键．防隔热材料高温热物性数据的准确测量是防隔热材料性能评价及可靠性评估的基础，对于提高我国的型号设计水平，满足我国航空航天及国防领域的标准数据需求等方面都具有重要的意义．

瞬态接触热源法[1-6]是一类重要的瞬态热物性测量方法，包括热线法、热带法、热探针法、阶越(脉冲)平面热源法、常功率平面热源法以及瞬态平面热源法等．该类方法具有快速、准确、可实现多参数测量、方式灵活多样、具有较宽的温度和热参数覆盖区间等许多优点，但将其应用于防隔热材料的热物性测量时，仍然存在以下5 点不足．

(1)高温测量上限较低，且中高温测量误差大．

(2)缺乏探头热容及时间延迟影响的充分考虑．

(3)接触热阻会受到众多因素的耦合影响，目前还主要采用涂抹填料或实验数据的预处理等手段减小接触热阻对测量的影响，非常欠缺从理论角度探察其对热物性测量的实际影响规律．

(4)瞬态接触热源法的快速测量是以被测试样达到热平衡为前提的，对于热导率及热扩散率很低的隔热材料来说，目前该类方法所采用的试样都较大，无法体现出瞬态接触热源法快速测量的优越性．

(5)瞬态接触热源法与其他非稳态方法一样，测量误差通常比稳态法大．这主要是由于测量过程往往很难完全满足所要求的边界条件，并且由此引入的误差不像稳态法那样易于理论描述和计算．

基于上述问题，本文提出了一种适用于防隔热材料高温高精度热物性测量的保护平面热源法，并通过建立一套防隔热材料高温热物性测量装置，来考察其对隔热材料热物性测量的实际使用性能．

1 测试原理及模型推导

设计的传热过程如图1 所示．初始温度均匀一致的两无限大平板，中间夹持一无限大薄膜热源；某一时刻开始，薄膜热源均匀释放大小已知的热流量，薄膜热源的温度将升高；温升速率的快慢将受到探头热容、时间延迟、接触热阻以及试样热物性的综合作用．

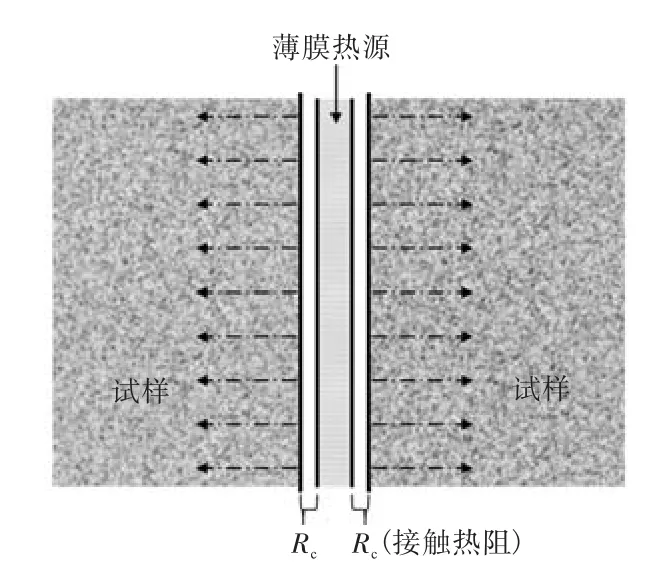
图1 无限大平板的一维热传导Fig.1 One demensional heat transfer of infinite plane plate

该热过程为一维热传导问题．假设薄膜热源的小扰动热流不会对热物性及接触热阻产生影响，将热物性及接触热阻视为常值；并假定热源很薄，有热容但无温度分布，将薄膜热源视为集总体处理；相应的导热微分方程、初始和边界条件分别为

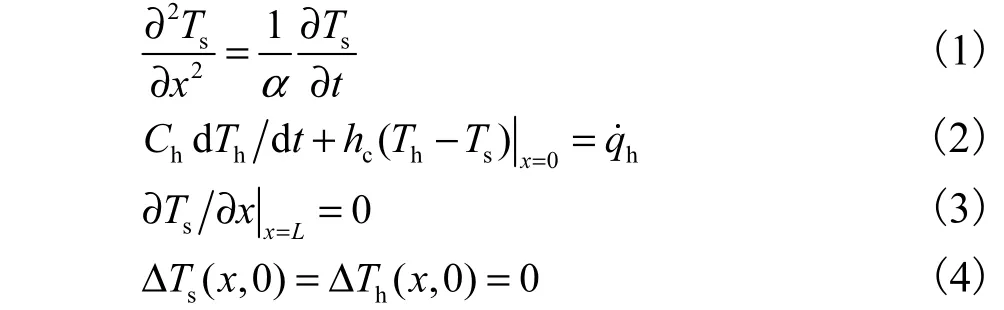
式中：T、 TΔ 为温度及过余温度，K；下标s 和h 分别代表试样和薄膜热源；α为热扩散率，m2/s；ch 为接触热导率，W/(m2·K)，cc1hR= ，cR 为接触热阻；hhh C m c=为热源单位面积热容，J/(m2·K)，hm 为单位面积质量，kg/m2，hc 为比热容，J/(kg·K)；hq˙为单面热流密度，W/m2；L 为平板厚度，m．

[7]求解微分方程组，得解析解为

式中：λ为热导率zn为式(6)的解，

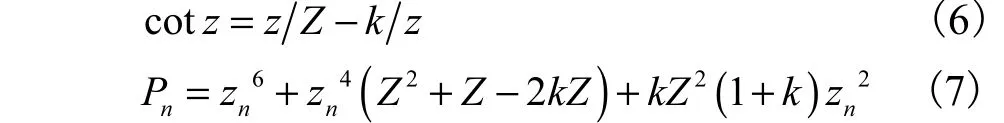
为得到热源的温升解析解，由式(2)分离变量得

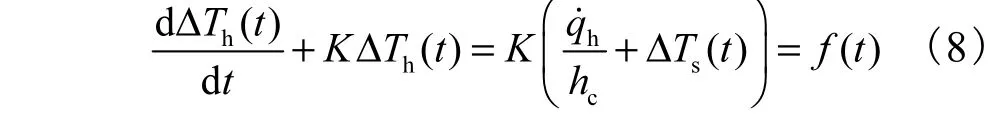
式中 c h/K h C= ．解齐次方程

得其通解为

式中C1为任意常数．

求解特解时，假定函数f(t)包含常数项、一次项及指数求和项，即

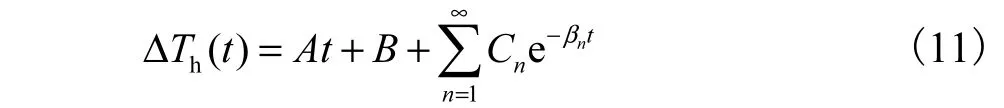
式中βn= znαL2．将式(5)代入式(8)，根据f(t)各项对应的相关系数，赋值A'、B '和 Cn'分别为

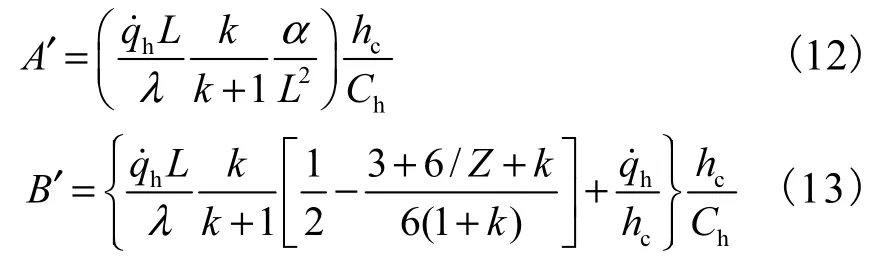
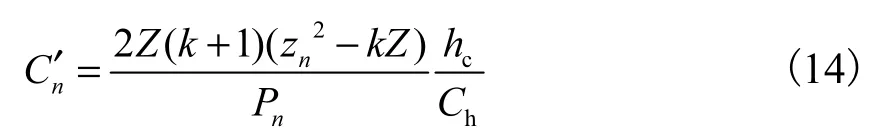
将式(11)代入式(8)，得系数A 、B 和 nC 分别为

得薄膜热源温度响应通解为

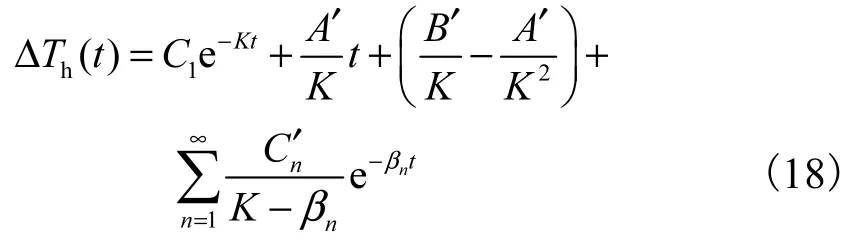
系数C1由初始条件式(4)确定为

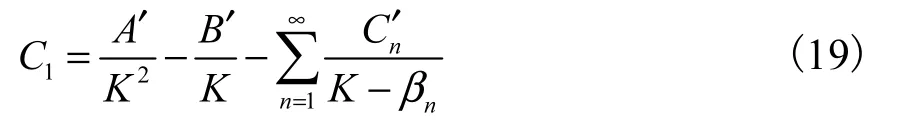
最终得到薄膜热源的温度响应解析解为

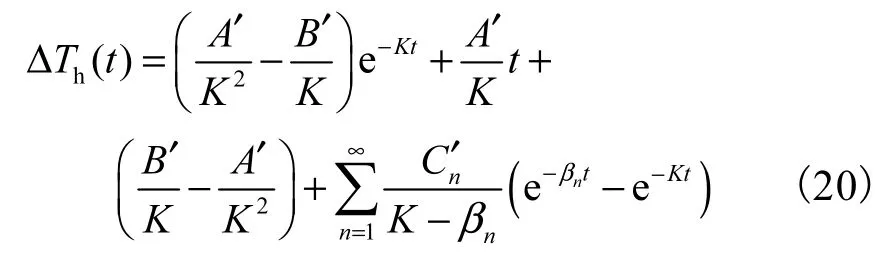
式(20)是建立在一维传热假设条件下的，实际测试时，为减少试样热平衡等待时间，必须限制试样的尺寸；对于有限尺寸试样，必然在边界产生热损，此时已不再是一维传热，会对热源温度响应造成影响，引起测量误差．

由于本文面向隔热材料，其热导率及热扩散率很低，在有限测量时间内，热损只能对试样外边缘一定区域的温度分布产生影响，而对于试样中心区域将不会产生较大影响，这一不受侧边界热损影响的中心区域为保护平面热源法的正确使用提供了保障条件，如图2 所示的中心灰色区域．

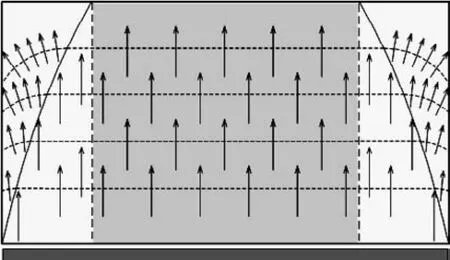
图2 存在热损时试样内等温线及热流分布Fig.2 Distribution of temperature contour and heat current Fig.2 when side heat waste happens

根据各种测量条件下的有限元分析结果，指导耐高温测温传感器结构的设计，综合考虑探头热容及时间延迟等影响因素对测量的影响，对式(20)理论温升模型进行修正，得到修正解析解为

式中：P0=I2R0，R0为初始电阻；S为探头的有效测量面积，S =πa2；并有

式中：t'为时间补偿后各测量点的对应时间；td为延迟时间，根据文献[8]的研究结论，时间延迟会随测量时间而变化，并有 0 ≤td≤0.005t，但一般不会超过0.1 s，即td≤0.1．

2 高温热物性测量装置

高温热物性测量装置的原理如图3 所示．主要包括：既是薄膜热源、又是温度传感器还能起到保护加热作用的耐高温探头(见图4)，实现对试样紧密夹持的耐高温试样夹持器(见图5)，能够提供稳定测量环境、减少漏热损失并有效防止试样高温氧化的高真空管式黑体炉(见图6)，以及高性能实验数据同步采集、处理及控制系统等．

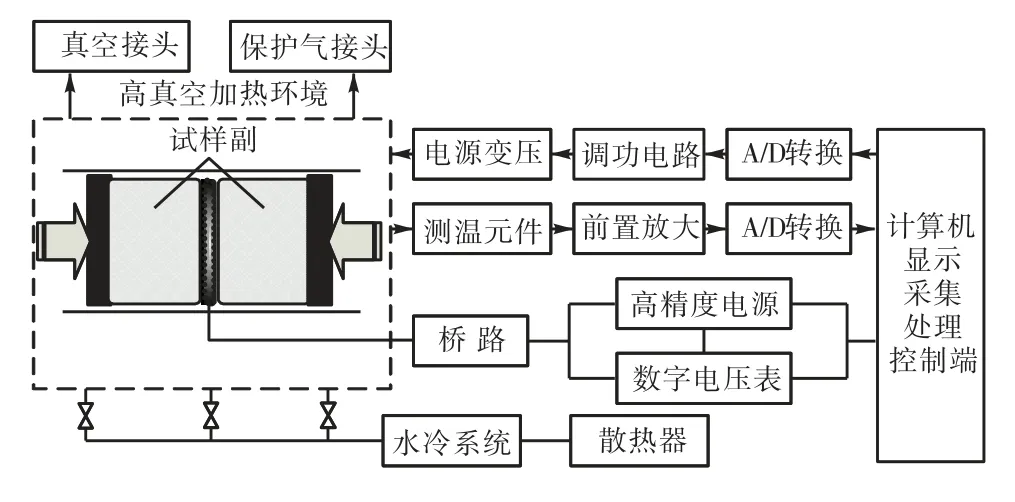
图3 测量装置原理Fig.3 Principle of experimental setup

测量使用的探头(见图4)基板采用yttria stabilized zirconia 8YSZ 耐高温陶瓷，厚度很薄，并具一定机械强度，可以认为满足集总体假设；基板两侧采用溅射技术覆1,µm 厚度铂金属膜，并通过激光刻蚀形成所需要的电流回路，两侧覆膜是为了保证对称性．采用铂金属作为发热热丝，其纯度很高，温度-电阻关联曲线接近线性，温度-电阻系数为4.6×10-3K-1[10]，不需要对温度-电阻关联式展开新的研究和推导．

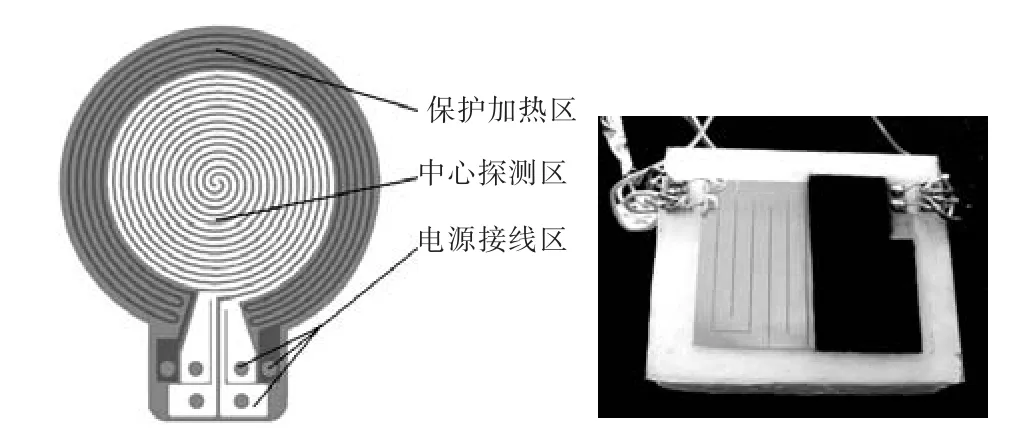
图4 保护平面热源法常温及高温实验探头Fig.4 Sensors of guarded plane source method in normal Fig.4 and high temperature experiments

保护热源探头设计有中心探测区及周边保护区，加热功能由保护区和探测区共同实现，测温功能则仅通过中心探测区实现．周边保护区的设计是为了保证一维热传导状态，保证绝热边界条件．

试样夹持器采用 Aremco 耐高温陶瓷材料，Aremco 耐高温陶瓷材料使用温度可达1,650,℃，高度致密且完全烧结，抗压强度为2.34×109Pa，抗弯强度为3.17×108Pa；除此之外，其导热系数较低，能够更好地保障保护平面热源法需要的绝热边界条件，并且可以实施机械加工，可以加工成所需要的结构形式．

图5 Aremco陶瓷夹持器Fig.5 Aremco ceramic holder

实验时，将耐高温探头、试样所组成的三明治结构置于试样夹持器中，将封头旋紧使得试样紧密接触；将试样夹持器置于管式黑体炉等温区，并将管式黑体炉抽成真空，真空度低于10-3Pa；而后，通电管式黑体炉，达到测试温度后控制于恒温状态持续加热；待试样温度均匀后，通电加热高温探头并实时采集温度信号，测量实验开始进行．

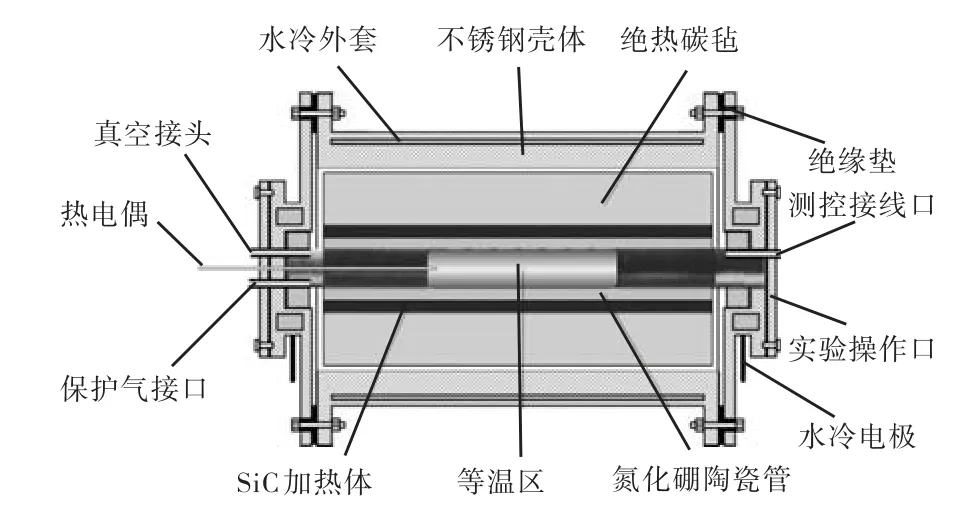
图6 管式黑体炉剖面Fig.6 Cross section of tubular blackbody furnace

3 实验结果及分析

3.1 标准材料常温热物性测量实验

为了对保护平面热源法进行准确的评价，利用研制的隔热材料多热物性测量装置对美国杜邦公司生产的SP1 级纯聚酰亚胺VespelTMSP1 材料的热导率和热扩散率进行了测量．VespelTMSP1 材料具有很强的耐磨性、长期尺寸稳定性和热稳定性，可以在室温至288,℃的范围内长期使用；并且类似金属铜，具有很好的机械加工性能．鉴于VespelTMSP1 材料物理性能稳定且各向同性，使得它成为目前国际上公认的热物理性能标准材料之一．

中常温范围内，VespelTMSP1 的热物理性参数如表1 所示[11]，采用试样尺寸为Φ30,mm×15,mm．

表1 VespelTM SP1热物性参数标准数据Fig.1 Standardized data of VespelTM SP1 against temperature

在测试温度(20±0.1)℃、加热功率0.2,W、测量时间为150,s 的测试条件下，对VespelTMSP1 标准材料进行了热物性测试．为了与中常温常压下的标准数据进行有效比对，实验不对管式黑体炉进行抽真空处理．在同一测量条件下，对VespelTMSP1 标准试样的热导率和热扩散率进行了多次测量，选取具代表性的2 次实验，测量结果如图7 和图8 所示．

2次实验的主要区别在于对试样夹持紧密程度的不同，通过控制试样夹持器的旋紧程度来实现试样与测温探头的不同接触紧密度，从而人为地控制接触热阻的大小，来评估接触热阻的实际影响．实验结果如表2 所示．

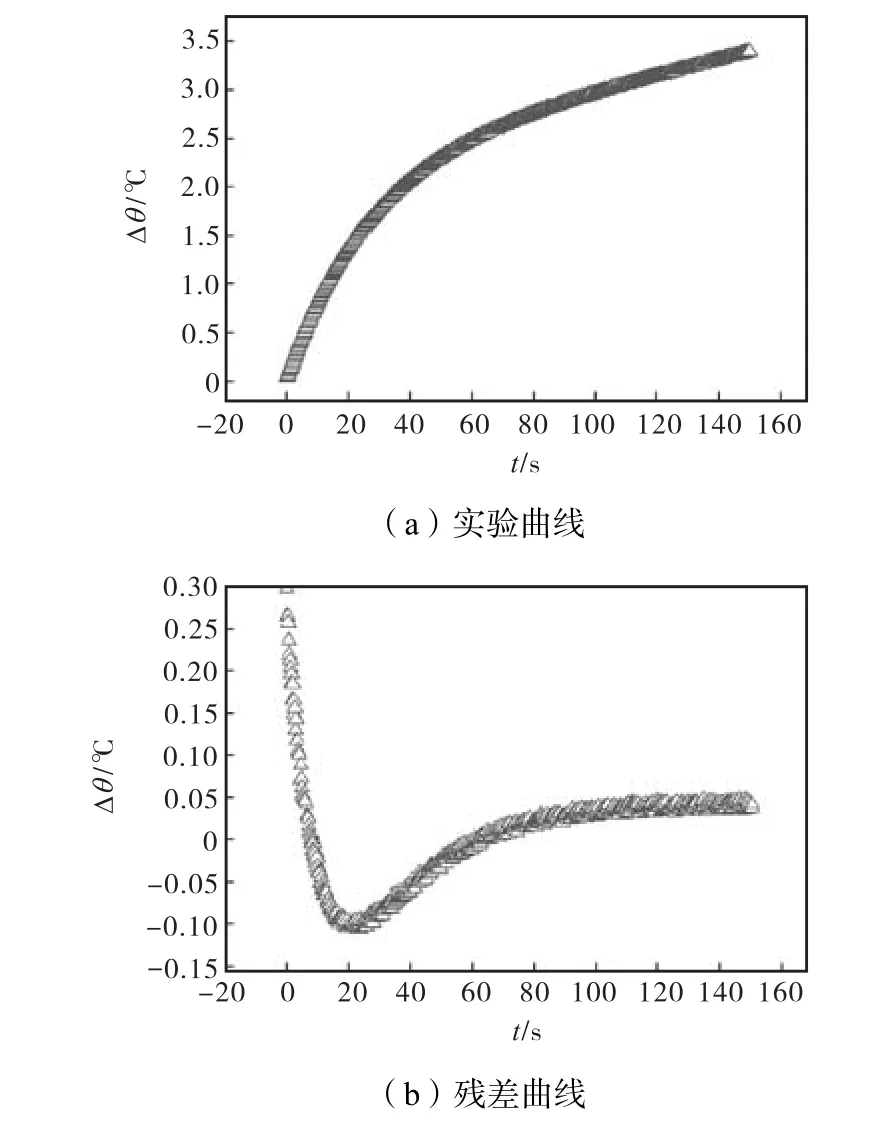
图7 实验曲线及残差曲线(1#)Fig.7 Experimental and residual curves (1#)

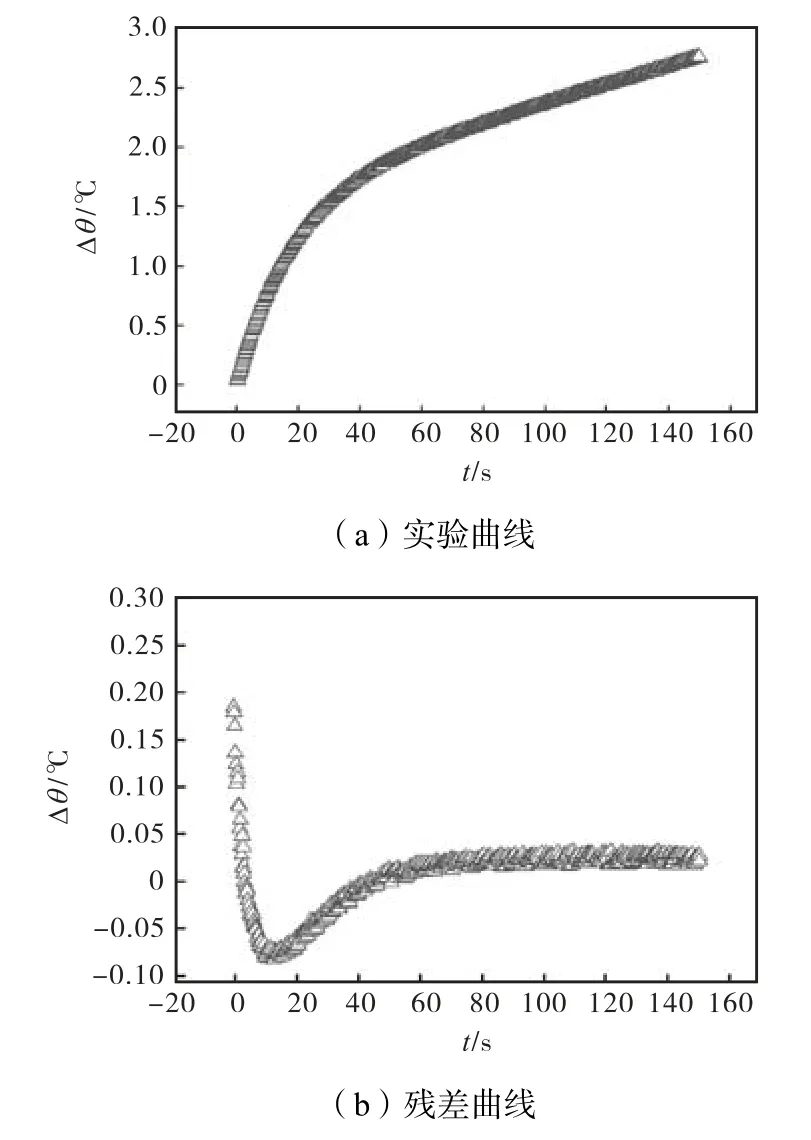
图8 实验曲线及残差曲线 (2#)Fig.8 Experimental and residual curves (2#)

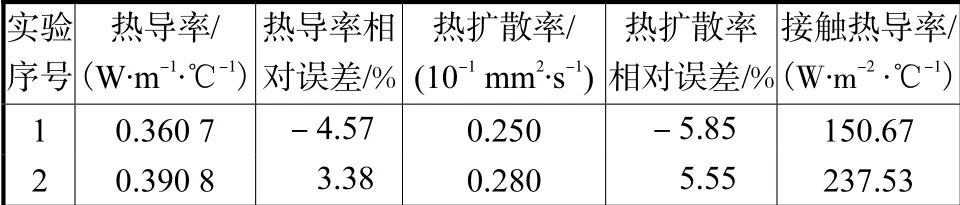
表2 实验1和实验2的测量结果Fig.2 Measurement results of experiments 1 and 2

3.2 某隔热材料高温热物性测量实验

在测试温度(1,200±0.1),℃、加热功率0.5,W、测量时间为750,s 的测试条件下，对某标准隔热材料进行测试，试样尺寸为Φ30,mm×30,mm，已知其在1,200,℃下的热导率λ＝1.10 W/(m·℃)，热扩散率α＝7.38×10-7m2/s．实验进行多次，选取其中2 次实验，测量结果如图9 和图10 所示[12]．

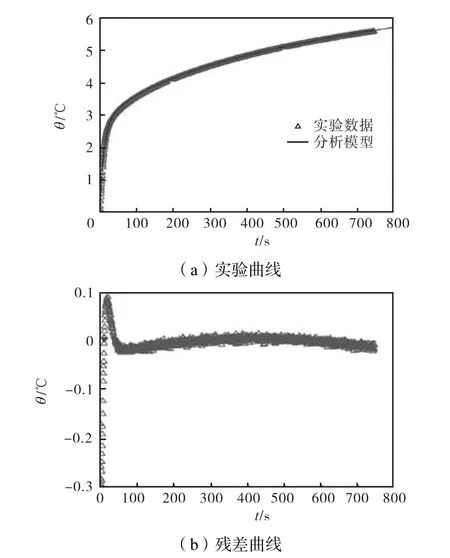
图9 实验曲线及残差曲线 (3#) Fig.9 Experimental and residual curves (3#)

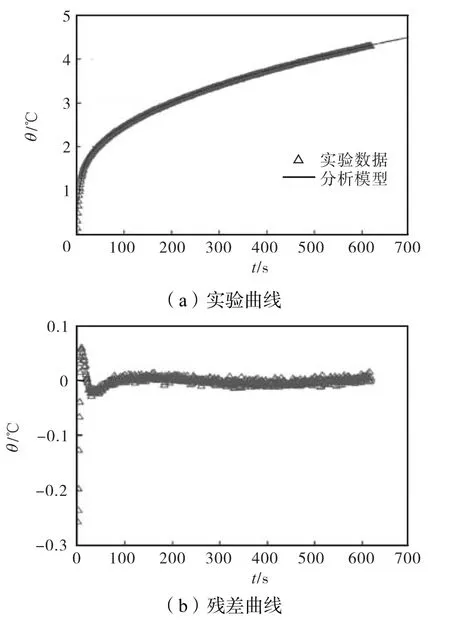
图10 实验曲线及残差曲线(4#)Fig.10 Experimental and residual curves (4#)

2 次实验的主要区别与实验1和实验2 一致，在于对试样紧密夹持程度的不同，实验结果如表3 所示．

表3 实验3和实验4的测量结果Fig.3 Measurement results of experiments 3 and 4

3.3 实验结果分析

(1) 分析图7～图10 残差曲线，残差均值不超过0.1,℃，表明实验数据与分析模型吻合良好．

(2) 分析表2 及表3 的测量结果，2 种标准材料在常温及高温测量条件下，热导率及热扩散率的测量值与标准数据吻合良好．常温相对误差均小于6%，能够满足隔热材料的基本工程需求(热导率测试误差为±8%，热扩散率测试误差为±8%)；高温相对误差最大值出现在测量热扩散率，仍小于10%．这表明保护平面热源法由于综合考虑了探头热容、时间延迟、接触热阻等因素对探头温升响应的实际影响，使得测量结果在常温及高温2 个测试温度下的测量结果相对误差较为稳定．

(3) 综合常温及高温段残差曲线及测量结果可知，在测量初始段，当接触热导率较小(接触热阻较大)时，测试初始温升阶越较大，残差曲线偏离量较大，热导率及热扩散率的测量精度较低；反之，当接触热导率较大时，测试初始温升阶越就较小，残差曲线偏离量较小，热导率及热扩散率的测量精度较高；表明虽然所提出的平面热源法可以同时考虑接触热阻的影响，但热物性测量结果显示此方法并不能完全消除接触热阻对热物性测量产生的影响．因而，在实际测量时保证探头与试样的紧密接触是提高热物性测量精度的关键．

(4) 观察测量初始段，实验数据与理论模型产生了明显偏差，表明所得到的保护平面热源法理论模型仍有不足，与实际传热过程还有差距．

(5) 残差分析表明，接触热阻的存在会对测量初期实验数据与分析模型造成较大的偏差．造成这种现象的原因是多方面的，有分析模型不能完全匹配实际测量实验的原因、有接触热阻非均匀分布的原因、还有微尺度内样品表面粗糙度造成微尺度对流、微尺度辐射等方式传播的原因等．

3.4 实验装置不确定度分析

按照国际标准ISO GUM 的定义方法，实验测量属于A 类不确定度分析，只能够代表温度测量数据与理论温升解析解的拟合程度，其本身不能反映误差的真正来源．因此对实验装置进行B 类不确定度的分析，不确定度的主要影响因素有：①温度测量引入的不确定度；②输出加热功率引入的不确定度；③探头热容测量引入的不确定度；④试样长度测量引入的不确定度；⑤时间计数所引入的不确定度．

温度的测量依赖于对铂金属加热丝两端电压变化的测量，主要受温度电阻关联式的影响．该装置探头采用高纯度铂金属制造，铂的电阻温度系数为常数4.6×10-3K-1，由温度测量引入的不确定度＜0.1%；所采用的Keithley 2400 精密电流源，可保证最大输出功率不确定度＜0.2%；采用德国耐驰同步热分析仪STA 449 测量探头热容，测量不确定度＜0.5%；采用0.5,µm 分辨力千分尺测量试样的长度，可保证测量不确定度＜0.005%；时间计数引入的不确定度，根据计时器的工作频率不超过0.1%．上述各项不确定度都服从正态分布且互不相关，根据扩展不确定度的合成法则，其合成不确定度小于1%．

4 结 语

本文提出了一种适用于防隔热材料高温热物性测量的保护平面热源法，该方法能够综合考虑探头热容、时间延迟以及接触热阻等因素对测量的影响．通过所研制的隔热材料高温热物性测量装置，对2 种标准材料分别在常温及高温进行了热物性测试；通过实验结果的分析、比对，理论模型与实测曲线吻合良好，且由于考虑了接触热阻，使得不同测量条件下的热物性测量准确度稳定性良好，但实际测量时保证探头与试样的紧密接触仍是提高热物性测量精度的关键．

参考文献：

［1］Healy J J，de Groot J，Kestin J. The theory of the transient hot-wire method for measuring thermal conductivity[J].Physica，1976，82：393-408.

［2］Yamasue E，Susa M，Fukuyama H，et al. Nonstationary hot wire method with silica-coated probe for measuring thermal conductivities of molten metals[J].Metallurgical and Materials Transactions A：Physical Metallurgy and Materials Science，1999，30(8)：1971-1979.

［3］Gustafsson S E，Karawacki E，Kahn M N. Transient hotstripe method for simultaneously measuring thermal conductivity and thermal diffusivity of solids and fluids[J].JPhys D：Appl Phys，1979，12：1411-1421.

［4］Kubicar L，Bohac V. Review of several dynamic methods of measuring thermophysical parameters[C]// 24th Int Conf on Thermal Conductivity /12th Int Thermal Expansion Symposium．Lancaster：Technomic Publishing Company，1990：135-149.

［5］Gustafsson S E. Transient plane source technique for thermal conductivity and thermal diffusivity measurements of solid materials[J].Rev Sci Instrum，1991，62：797-804.

［6］Hideaki N，Mikito M，Martin C，et al. Effect of thermal convection on the measurement of thermal conductivity of molten Bi and Sn by the hot-disk method[C]//Sixth Japan/China Workshop on Microgravity Sciences．Takeo Onsen，Saga，Japan，2005：132-137.

［7］Carlaw H S，Jaeger J C.Conduction of Heat in Solids[M]. New York：Oxford Univ Press，1959.

［8］He Yi. Rapid thermal conductivity measurement with a hot disk sensor (Part 1)：Theoretical considerations[J].Thermo Chimica Acta，2005，436：122-129.

［9］Beck J V，Arnold K J.Parameter Estimation in Engineering and Science[M]. New York：John Wiley，1977：23-36.

［10］王魁汉. 温度测量实用技术[M]. 1 版. 北京：机械工业出版社，2007：34-81.Wang Kuihan.Operative Technology on Temperature Measurement[M]. 1st ed. Beijing：China Machine Press，2007：34-81(in Chinese).

［11］Fedore R ，Stroe D. Thermophysical properties of vespelTMSP1[C]//Proceedings of the27th International Thermal Conductivity Conference and the15th International Thermal Expansion Symposium．Knoxville，USA，2003：813-816.

［12］Bovesecchi G，Coppa P. High temperature(till 1 500℃)contemporary thermal conductivity and thermal diffusivity measurements with step flat heat source[C]// Tan Jiubin，Wen Xianfang. Fifth International Symposium on Instrumentation Science and Technology．Shenyang ，China，2009：7133.