混凝土灌芯玻璃纤维增强石膏墙板的简化计算
马清珍,姜忻良,张宝魁
(1. 天津大学建筑工程学院,天津 300072;2. 天津商业大学商学院,天津 300134)
玻璃纤维增强石膏板是由澳大利亚开发、生产的一种建筑板材,是用熟石膏、工业附属产石膏、无碱玻璃纤维及化学添加剂为原料,在工厂制作,并可将生产的板材运至现场进行快速拼装施工.其成品的规格为12,m×3.05,m×0.12,m,两侧面是13,mm 厚的石膏纤维薄板,中间为薄板形成的空腔,沿长度方向每隔250,mm 布置一个厚20,mm 的石膏隔板,隔板将板的空腔分割成230,mm×94,mm 的孔洞.这些孔洞可以通过填充岩棉、聚苯乙烯泡沫、混凝土等材料使板满足保温、隔热、防火、隔音、承重等不同技术要求[1].由于其施工速度快、施工工艺简单、质量高,所以它可以代替砖瓦、砌块结构,节省土地和能源.
混凝土灌芯玻璃纤维增强石膏墙板(以下简称复合墙板),指的是在玻璃纤维增强石膏墙板的空腔中灌入混凝土,同时在每个空腔中布置2 根或1 根竖向钢筋.这种复合墙板可作为大型建筑结构的剪力墙,承受竖向荷载和水平荷载.在复合墙板的受力过程中,当复合墙板处于不同工作阶段时,不但石膏板与钢筋混凝土各自所处的阶段不同,而且这两类材料之间相互作用也不同.若按实体单元进行建模,往往单元数量太多以致计算量过大,并有不易收敛等问题.对由该种复合墙板构成的大型结构计算,更是无法实施.为便于工程实际结构的计算,笔者建立了一种简化计算模型.
1 宏观计算模型
计算模型采用多垂直杆元模型(见图1)[2-3].在这个模型中,刚性梁主要模拟结构中的圈梁,由多个相互平行的垂直杆相连,垂直杆代表复合墙板的轴向承载力、弯曲承载力,承受施加在复合墙板上的竖向荷载和部分水平荷载,位于0.5h处的水平弹簧代表了复合墙板的剪切承载力,主要承受施加在复合墙板上的水平荷载.
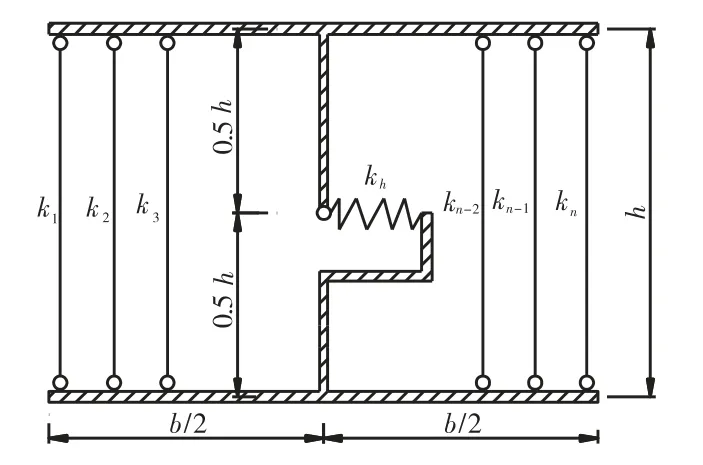
图1 多垂直杆元模型Fig.1 Multi-vertical-line-element model
2 垂直杆元荷载-位移骨架曲线及滞回模型
2.1 垂直杆元荷载-位移骨架曲线
将垂直杆元布置在芯柱中心的位置,具体的垂直杆元荷载-位移骨架曲线如图2 所示.

图2 垂直杆元的荷载-位移骨架曲线Fig.2 Load-displacement skeleton curves of vertical-line element
拉区部分,初始刚度为

式中:L为复合墙板高度;eqE 为复合墙板的等效弹性模量,假定墙板开裂时,钢筋、混凝土、石膏板变形相同,可推得

式中:A=AC+AP+AS;AC为芯柱混凝土横截面面积;AS为芯柱钢筋横截面面积;AP为芯柱纤维石膏横截面面积;EC为混凝土的弹性模量,以试验值为准;ES为钢筋的弹性模量,以试验值为准;EP为纤维石膏板的弹性模量,以试验值为准.
轴力杆开裂时的位移为

复合墙板屈服时假定钢筋同时发生屈服,则

式中:dsy为复合墙板屈服位移;Kse为复合墙板开裂后的刚度,结合复合墙板试验的实际情况,设定屈服之后的抗拉刚度为初始刚度的 0 . 0 2 倍,即Ksy= 0.02Kse,Ksy为复合墙板屈服之后的刚度;εp为空心石膏板开裂时的应变,根据试验取0.000,3;ψ0为应力不均匀系数,见《混凝土结构设计规范》(GB 50010—2002);fy为钢筋轴向抗拉强度,以试验值为准.
压区部分,初始刚度为

轴力杆受压屈服时的位移为

轴力杆屈服后所能承受的稳定残余力为

不再考虑石膏的抗压作用,轴力杆达到稳定残余力时的位移为

式中:cε为混凝土峰值压应变,取0.002;cf为混凝土轴向抗压强度,以试验值为准.
2.2 垂直杆元荷载-位移滞回模型
在对复合墙板结构进行动力弹塑性分析时采用SAP2000 程序,垂直杆元在中部设置轴力塑性铰,以考虑垂直杆元的塑性变形.由于塑性铰是刚塑性的,因此垂直杆在弹性阶段,无论是卸载状态还是重新加载状态,塑性铰内部都不会发生任何变形,所有的弹性变形均发生在垂直杆内.当垂直杆产生塑性变形时,塑性变形将在塑性铰内部发生.塑性铰的加载卸载规则采用程序默认的方式[4].
3 剪切单元荷载-位移骨架曲线计算及滞回模型
无论是满灌混凝土石膏复合墙板还是隔孔灌混凝土石膏复合墙板,其骨架曲线均采用三折线,如图3 所示.图中Vr、Vy为侧向开裂荷载和屈服荷载.

图3 剪切杆元荷载-位移骨架曲线Fig.3 Load-displacement skeleton curves of shear element
3.1 满灌混凝土石膏复合墙板的剪切骨架曲线
满灌混凝土石膏板剪切骨架曲线的初始刚度、开裂后刚度和屈服后刚度分别为

式中:Geq为满灌混凝土石膏复合墙板的等效剪切模量;α为混凝土和石膏板之间的黏结滑移影响系数,经过与试验结果的比较并试算得α=0.06;λ为轴压比,λ=N/(fcA),N为单个混凝土芯柱承受的竖向荷载,假设作用在试件上的总竖向荷载平均分配在每个混凝土芯柱上,A0为满灌混凝土石膏板的横截面面积,通过试验[5]以及文献[6]的结论,可以得出随着轴压比的增加,复合墙板的抗剪刚度也在增加;k 为截面剪应力非均匀分布修正系数,对于矩形截面取1.2;β0、β1为刚度折减系数,灌芯石膏板开裂后由于混凝土和石膏板之间出现了滑移,抗剪刚度开始下降,结合试验情况,β0、β1分别取0.3、0.2.
3.1.1 满灌混凝土石膏复合墙板等效剪切模量的推导
满灌混凝土石膏复合墙板是一种复合材料,其Geq的计算,以文献[7]为基础,采用等应变假设进行推导.
取一孔复合墙板作为分析单元,由于对称性,取1/4 模型进行分析,为了更简明地进行分析,将模型划分为Ⅰ、Ⅱ、Ⅲ 3 个区域.图4为满灌复合墙板等效剪切模量Geq的推导示意.

图4 满灌复合墙板等效剪切模量的计算Fig.4 Equivalent shear elasticity calculation of the concrete filled panels
假定Ⅰ、Ⅱ区具有相同的纵横向微观剪应变,该假设保留1-1 面上存在剪应力不相容,设Gc、Gp分别表示混凝土和纤维石膏的剪切模量.
静力相当条件为
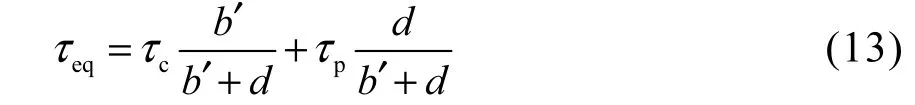
几何方程为

物理方程为



3.1.2 侧向开裂荷载和屈服荷载的求取
混凝土芯柱之间的玻璃纤维增强石膏对复合墙板的抗剪起着非常重要的作用,它相当于芯柱之间的一个连接单元,复合墙板的抗剪强度主要就是由石膏板的纵向剪切强度来决定,满灌的复合墙板在侧向荷载作用下最终以芯柱之间的这个连接单元发生破坏作为其剪切破坏的标志,与混凝土的强度以及配置的钢筋关系不大,如表1(单向加载,无轴向荷载)和表2所示(加轴向荷载).轴向荷载能够有效地提高复合墙板的抗剪能力.本文考虑轴向荷载的影响,确定复合墙板的极限抗剪承载力为

式中:uq为无轴向荷载影响的复合墙板抗剪强度,根据表1 的结论,取67.66,kN/m;N0为初始轴向荷载;b为板的宽度.
构件的骨架曲线反映了构件的开裂强度(对应于开裂荷载)和极限强度(对应于极限荷载),但是骨架曲线上没有明显的屈服点,根据文献[5,8-9]中复合墙板构件的剪切试验曲线,确定墙板的屈服抗剪承载力为极限抗剪承载力的75%,墙板的开裂荷载Vr为侧向极限荷载Vu的60%.
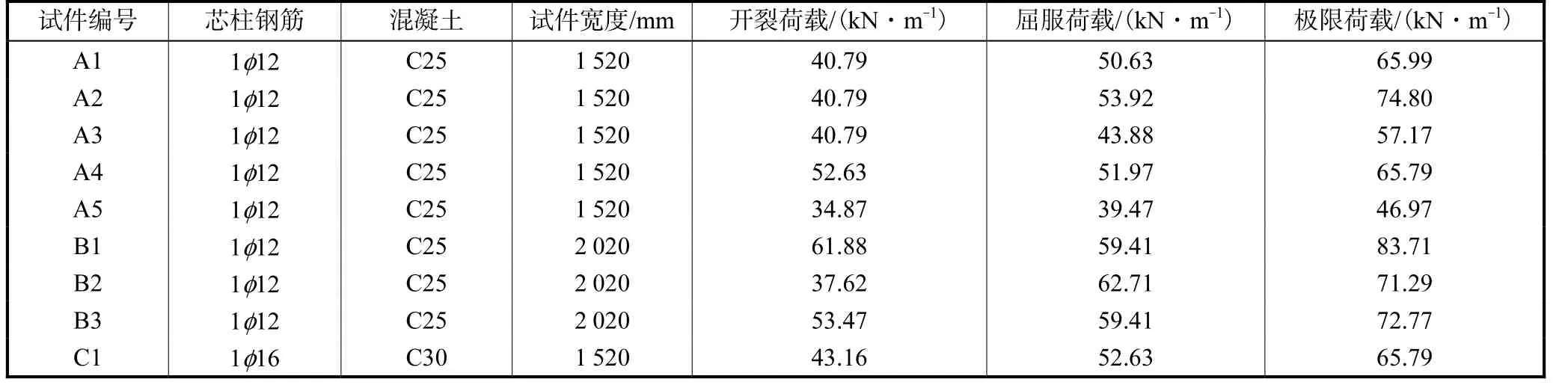
表1 满灌复合墙板试件试验及计算结果(单向加载,无轴向荷载)Tab.1 Test and calculating results of the concrete filled panels specimen(monotonic shear tests,without axial load)

表2 满灌复合墙板试件试验及计算结果(加轴向荷载)Tab.2 Test and calculating results of the concrete filled panels specimen(with axial load)
3.2 隔孔灌混凝土石膏复合墙板的剪切骨架曲线
隔孔灌混凝土石膏复合墙板剪切骨架曲线的初始刚度、开裂后刚度和屈服后刚度分别为
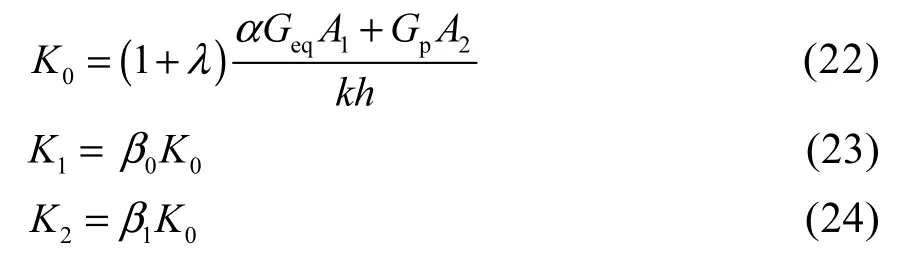
式中:λ、α、Geq、k、0β和 1β的意义及计算方法同满灌混凝土石膏复合墙板;A1为复合墙板中灌孔复合部分的总横截面积;Gp为纤维石膏板的剪切模量;A2为复合墙板中除去灌孔复合部分、空腔部分后的总横截面积.根据表3 隔孔灌复合墙板试件试验及计算结果(反复加载,有轴向荷载),开裂荷载取58.11,kN/m,屈服荷载取64.32,kN/m.

表3 隔孔灌复合墙板试件试验及计算结果(反复加载,有轴向荷载)Tab.3 Test and calculating results of the partial concrete filled panels specimen (cyclic shear tests,with axial load)
3.3 剪切单元荷载-位移滞回模型
剪切单元的滞回模型采用SAP2000 程序中的Pivot 模型,结合复合墙板反复加载试验曲线形状,模型中的系数取值为
4 灌芯玻璃纤维增强石膏复合墙板非线性分析
4.1 复合墙板pushover分析
笔者应用上文提到的多垂直杆元模型对天津大学[5,9-10]、亚阿德莱德大学[8]所做的灌芯玻璃纤维增强石膏板进行了pushover 计算,计算得到的满灌复合墙板侧向荷载-位移曲线(无轴向荷载)如图5 所示,计算得到的满灌复合墙板侧向荷载-位移曲线(有轴向荷载)如图6 所示,计算得到的隔孔灌复合墙板侧向荷载-位移曲线(有轴向荷载)如图7 所示.

图5 满灌复合墙板侧向荷载-位移曲线(无轴向荷载)Fig.5 Lateral load-displacement curves of the concrete Fig.5 filled panels(without axial load)
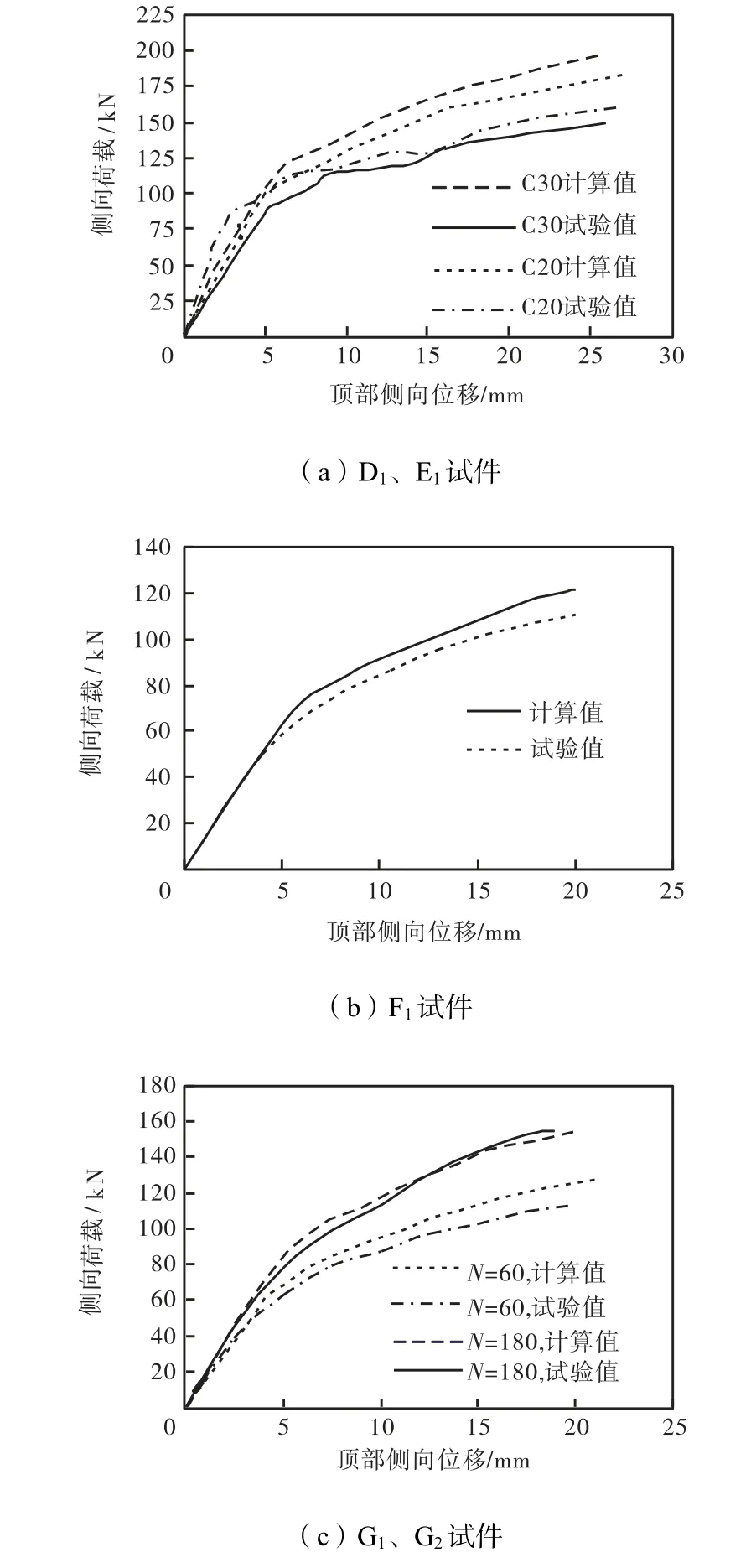
图6 满灌复合墙板侧向荷载-位移曲线(有轴向荷载)Fig.6 Lateral load-displacement curves of the concrete Fig.6 filled panels(with axial load)
从计算曲线和试验曲线的对比分析可以得到以下3 点结论.
(1) 满灌、无轴向荷载复合墙板的计算曲线和试验曲线基本一致.
(2) 满灌、加轴向荷载复合墙板的计算曲线和试验曲线基本一致.图6(b)和(c)的试验曲线和计算曲线符合得比较好,图6(a)中C30 的误差较大,这可能与试件本身的质量有关.
(3) 隔孔灌复合墙板的计算曲线和试验曲线基本一致.图7(a)中C20 的计算曲线开始阶段和试验曲线吻合得很好,但在屈服和极限阶段试验曲线要低于计算曲线,误差比较大,这可能与试件本身的质量有关.图7(c)中的C30 计算曲线和试验曲线之间的误差要大,其试验曲线明显高于计算曲线,这可能与试件本身的质量有关.

图7 隔孔灌复合墙板侧向荷载-位移曲线(有轴向荷载)Fig.7 Lateral load-displacement curves of the partial concrete filled panels(with axial load)
4.2 复合墙板动力弹塑性分析
笔者应用上面提到的多垂直杆元模型对天津大学[4]制作的复合墙板进行了动力弹塑性计算,计算得到复合墙板的荷载-位移骨架曲线如图8 所示.
从计算曲线和试验曲线的对比分析可以得到:复合墙板的计算曲线和试验曲线基本一致.个别的误差较大,这可能与试件本身的质量有关.

图8 复合墙板侧向荷载-位移曲线(反复加载,有轴向荷载)Fig.8 Lateral load-displacement curves of the composite panels(cyclic shear tests,with axial load)
5 结 论
(1) 应用多垂直杆元模型进行灌芯复合墙板的非线性计算简单有效,力学概念清晰直观,建模简便,又具有较好的计算精度,有利于工程中的实际应用.
(2) 在计算由该类复合墙板构成的整体结构时,考虑到工程应用,对于满灌复合墙板,可在上述宏观计算模型的基础上,对垂直杆元作进一步简化,将模型中内部的垂直杆元(2~n/2 杆和n/2+1~n-1 杆)分别向其中心进行简化,形成五垂直杆元宏观计算模型.本文对这种五垂直杆元宏观计算模型进行了非线性分析验算,和不简化的宏观计算模型相比,两者的底部剪力-顶点位移曲线非常接近,所以,可用五垂直杆元宏观计算模型进行整体结构建模.
(3) 在计算模型的剪切刚度时,通过折减系数考虑了纤维石膏和混凝土之间的黏结滑移作用,而且还考虑了轴压比的影响,使计算模型和实际受力情况比较符合.
(4) 混凝土灌芯石膏复合墙板是一种复合板材,本文以细观力学矩形模型为基础,采用等应变假设推导了等效剪切刚度,对类似的由2 种以上刚度相差悬殊的材料组成的结构计算有一定的借鉴意义.
[1]Wu Yufei. The effect of longitudinal reinforcement on the cyclic shear behavior of glass fiber reinforced gypsum wall panels :Tests[J].Engineering Structures,2004 ,26(11):1633-1646.
[2]Vulcano A,Bertero V V,Colotti V. Analytical modeling of R/C structural walls[C]//Procs9th World Conference on Earthquake Engineering. Japan,1988,6:41-46.
[3]Kim Tae-Wan,Foutch D A,LaFave J M. A practical model for seismic analysis of reinforced concrete shear wall buildings[J].Journal of Earthquake Engineering,2005,9(3):393-417.
[4]金土木软件技术有限公司. SAP2000 中文版使用指南[M]. 北京:人民交通出版社,2006.Civil King Software Technology Company Limited.SAP2000Tutorials[M]. Beijing:China Communications Press,2006(in Chinese).
[5]刘 康.混凝土灌芯纤维增强石膏板抗震性能的试验研究及有限元分析[D]. 天津:天津大学建筑工程学院,2003.Liu Kang. Experimental Research and Finite-Element Analysis on the Seismic Performance of Fiber-Reinforced Plasterboard Filled with Concrete[D]. Tianjin:School of Civil Engineering,Tianjin University,2003(in Chinese).
[6]李宏男,李 兵. 钢筋混凝土剪力墙抗震恢复力模型及试验研究[J]. 建筑结构学报,2004,25(5):35-41.Li Hongnan,Li Bing. Experimental study on seismic restoring performance of reinforced concrete shear walls[J].Journal of Building Structures,2004,25(5):35-41(in Chinese).
[7]刘锡礼,王秉权. 复合材料力学基础[M]. 北京:中国建筑工业出版社,1984.Liu Xili,Wang Bingquan.Basis of Composite Mechanics[M]. Beijing:China Architecture&Building Press,1984(in Chinese).
[8]Wu Yufei, Dare M P. Axial and shear behavior of glass fiber reinforced gypsum wall panels:Tests[J].Journal of Composites for Construction,ASCE,2004,8(6):569-578.
[9]岳建伟,姜忻良. 速成墙板的抗剪性能试验研究[J].华中科技大学学报:城市科学版,2006,23(1):27-30.Yue Jianwei,Jiang Xinliang. Tests of shear performance of rapid walls[J].Journal of Huazhong University of Science and Technology:Urban Science Edition,2006,23(1):27-30(in Chinese).
[10]姜忻良,邓永胜. 纤维石膏板中不同间距灌注混凝土芯柱抗震性能试验研究[J]. 地震工程与工程震动,2004,24(4):110-114.Jiang Xinliang,Deng Yongsheng. Experimental study on seismic behaviors of fiber plasterboards with concrete core columns with filled different spacings[J].Earthquake Engineering and Engineering Vibration,2004,24(4):110-114(in Chinese).

