不同作用力下高桩码头叉桩受力分析

唐东洋 ，翟钢军 ，熊洪峰

（1.大连理工大学建设工程学部，大连116024；2.交通部天津水运工程科学研究所水工构造物检测、诊断与加固技术交通行业重点实验室，天津300456；3.哈尔滨工程大学船舶工程学院，哈尔滨150001）

随着我国经济的持续增长，天津港货物吞吐量迅猛增长，同时船舶向大型化发展。为满足超过原设计船型的船舶停靠，天津港对码头前沿水域和航道进行了浚深，这必然给码头结构带来不利影响。天津港2009年秋季检查结果［1］显示，高桩码头的许多叉桩出现了不同程度的断桩现象。

由于天津港为软土地基类型，高桩码头应用极广，其中叉桩是抵抗码头水平作用力的重要构件。影响高桩码头叉桩受力的因素有很多，包括码头自重、船舶撞击力及系缆力、码头前沿水域的浚深及码头岸线的回淤量、后承台和后方堆场的竖向荷载等，其影响程度各不相同。通过正交分析可以确定对计算结果影响较显著的因素，即叉桩受力计算中的敏感因素，对寻找叉桩破损原因和结构的优化设计有十分重要的意义。

本文采用数值计算方法分析高桩码头叉桩在桩土相互作用下的受力情况［2］。

1 高桩码头叉桩结构及工程概述

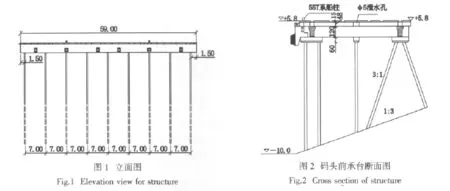
高桩码头结构对地基要求低，无需对地基进行复杂的工程处理，另外对航道疏浚和港池浚深适应能力强。其中叉桩是用来抵抗码头承受水平力荷载的重要构件，桩体的倾斜布置能使码头承受的水平力转换为叉桩的轴向力，并通过叉桩传到土体，进而使码头在水平力作用下产生很小的水平位移。某高桩码头，排架间距为7 m，承台宽度为13.8 m，直桩为55 cm×55 cm空心桩，叉桩为50 cm×50 cm空心桩，叉桩水平转角为22°，面板厚度为48 cm，码头结构段立面图见图1，结构段断面图见图2。

2 模型的建立

2.1 几何模型的建立及网格划分

采用ANSYS软件进行分析，建立高桩码头结构和地基土共同作用的整体三维有限元计算模型［2］，沿码头岸线方向取7 m，岸-海方向取90 m范围（码头前沿外-10 m，码头前沿往后取-80 m）。模型坐标轴取从码头前沿朝向后方堆场的方向为X轴正方向；Y轴正方向竖直向上；Z轴方向垂直于XY平面。

为方便计算，对空心桩进行一定的简化［3］，采用等效截面和刚度的实体方桩替代空心桩，面板、横梁、纵梁、帽梁、直桩、叉桩采用Solid65单元离散，土体由Solid45单元进行离散［4］。

2.2 材料参数及本构模型

计算分析中混凝土构件（桩、梁、板）、抛石等均考虑为线弹性材料，其材料特性按照我国相关技术规范取值，混凝土结构材料特性见表1；地基土体在计算分析中考虑为D-P弹塑性本构模型，土体参数根据《天津港22～24段码头工程岩土工程勘察报告》取值，土体材料特性见表2。

表1 上部结构材料特性Tab.1 Materials properties of upper structure

2.3 桩土接触面模拟

桩土接触变形问题属于边界条件非线性问题。在本文建立的有限元模型中，桩—土接触面采用面与面接触的Targe170，Conta173单元来模拟，该单元的特点是能进行较大的张开、滑移等大变形计算［5］。

通过KEYOP（12）中的选项设置，选择罚函数法作为接触面的算法。罚函数法是通过接触刚度在接触力与接触面间的穿透值（接触位移）间建立力与位移的线性关系

式中：CP，CT，SFRIC分别为接触压力、接触渗透和接触摩擦力；FKN，SLIDE，Mu，PRES分别为接触单元的接触刚度、接触位移、摩擦系数和法向接触力。

由式（1）～式（3）可知，接触界面的2个重要的力学参数——摩擦系数Mu和法向刚度FKN控制了接触的力学行为，因此这2个参数的正确取值是接触模拟正确的关键。作为非线性的接触问题，FKN取值无成熟经验可循，只能采用试算的方法确定。考虑到FKN越小，计算越容易收敛，先用一个比较小的FKN开始计算，收敛后再改大些。由于接触刚度FKN越大，则穿透越小、结果越合理，因此把FKN改大些重新计算，直到有一个满意的结果。

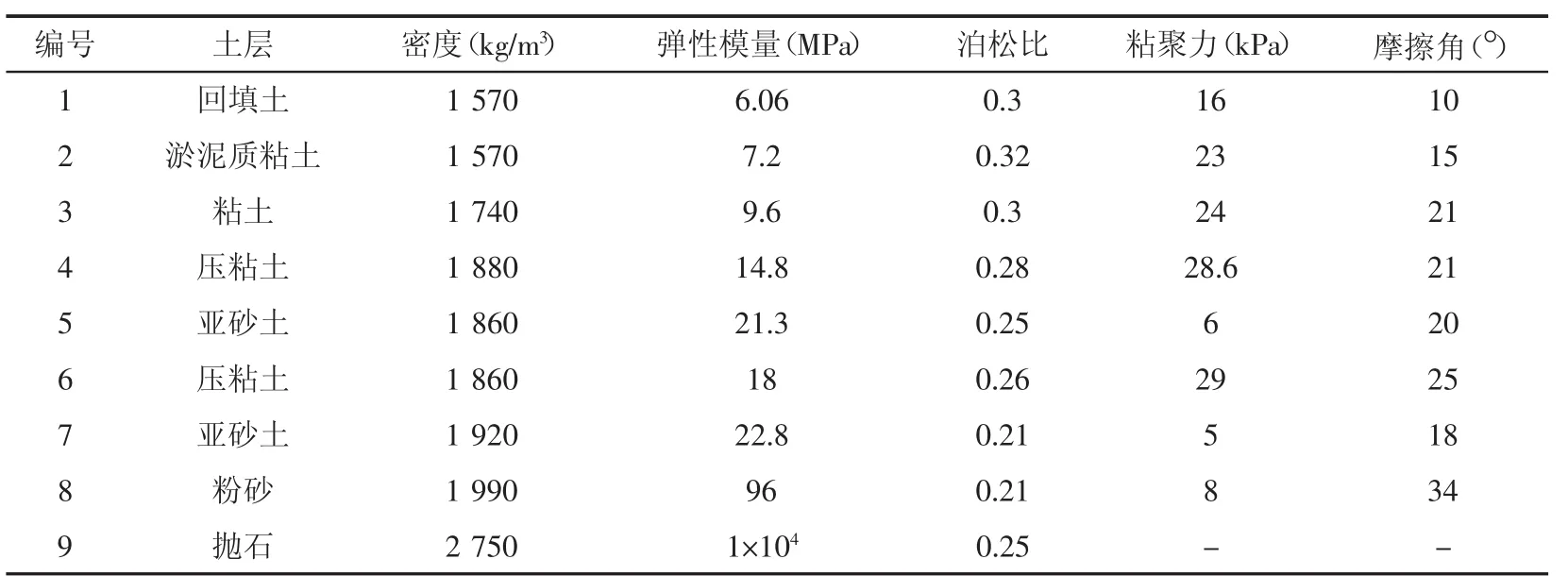
表2 土体材料特性Tab.2 Materials properties of soil

甘立刚等［6］对混凝土与土之间的摩擦系数做过大量试验，经过回归分析后得出桩土摩擦系数（表3）。

表3 桩土摩擦系数Tab.3 Friction coefficient of piles and soil

2.4 作用力

根据《港口工程荷载规范》（JTJ215-98）［7］，并结合现场观测，最后计算得到作用于单个排架下的最大船舶撞击力为183.2 kN，最大系缆力沿码头横向的分力为-126 kN；根据资料选取码头前沿最大浚深为-11 m，根据《天津港2009年秋季检查报告》［1］测得的岸坡形式计算回淤量；后承台及后方堆场的最大竖向荷载采用设计荷载5 t/m2。

3 叉桩受力分析

根据《2009秋季天津港检查报告》［1］可知，前承台叉桩在其桩顶附近出现了大量的宽裂缝，即断桩现象。为了寻求断桩原因，对叉桩桩顶受力进行分析。

3.1 正交化分析方法

为了避免重复分析、尽量减少试验的次数，采用具有均值和标准差敏感性因子计算方法的正交试验法进行分析。通过事先设计好的一套“正交表”来安排试验，借助正交表可以选出具有代表性的试验，以较少的试验次数取得的试验数据进行统计分析，而能得到满意的结果［8］。

为了得到叉桩桩顶受力随外力变化的规律和各外力对桩顶受力的敏感性程度，将影响叉桩受力的各因子（A为码头前沿水域的浚深及码头岸线的回淤量；B为船舶撞击力及系缆力；C为后承台和后方堆场的竖向荷载）均分为3个水平，进行正交分析；为了得到更精确的分析结果并减少试验次数，撞击力与系缆力分别与其他2个因子进行搭配计算。受力因子见表4和表5。

表4 撞击力组Tab.4 Impact force group

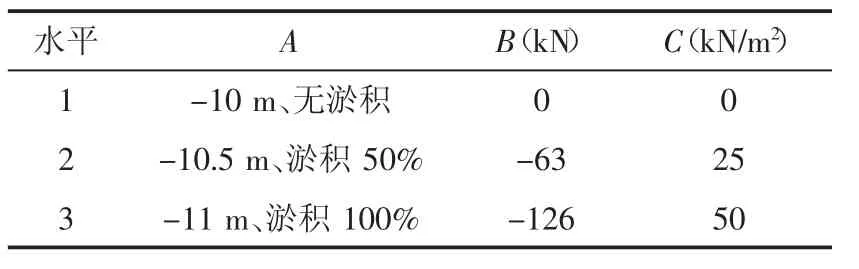
表5 系缆力组Tab.5 Mooring force group

本试验是三水平三因子的试验，故选择列数不能少于三列的正交表格，在三水平正交表中，列数不少于三的最小正交表是L9（34）（表6）。由表6可知，原本三水平三因子的不同搭配共有27组不同的试验，现在只需9组试验计算分析就能反映全面的情况。

3.2 计算结果分析

为模拟桩土摩擦，桩体采用了三维实体单元，后处理中实体单元不能提取结构内力，需进行二次开发编制APDL语言，对截面进行积分而得到叉桩结构内力，并通过坐标转换，将其模型坐标下的受力转换到叉桩正截面的受力。本文计算了叉桩桩顶垂直于轴向方向的截面（正截面）MZ、MX、FY、FX的受力，其正截面坐标俯视图见图3。MZ的正方向表示使沿X轴正方向的面受拉，MX的正方向表示使沿Z轴正方向的面受拉，FY方向为桩体受压为负，受拉为正；FX的正方向与X轴保持一致。

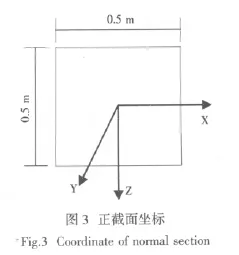
表6 向岸斜桩MZ试验及分析的正交表格Tab.6 Orthogonal table of the inclined piles for MZ experiment and analysis

表7为撞击力试验组下向岸斜桩受到的弯矩MZ，其中Ⅰj表示第j列“1水平”所对应的数据之和；Ⅱj表示第j列“2水平”所对应的数据之和；Ⅲj表示第j列“3水平”所对应的数据之和。以MZ第3列的数据为例，Ⅰ3/3是1，6，8三个试验所对应数据的平均值，而在这3次试验中A和C的水平都只出现了一次，Ⅱ3/3、Ⅲ3/3也是如此，因此3个平均数Ⅰ3/3、Ⅱ3/3、Ⅲ3/3的差别只反映了B1、B2、B3的差别。由于Ⅰ3/3、Ⅱ3/3、Ⅲ3/3的值逐渐增大，说明其结果随着B因子的增大而逐渐增大；用因子各水平所对应的平均值Ⅰ3/3、Ⅱ3/3、Ⅲ3/3可以评定该因子的变化对结果产生的一定规律，并评定该因子取哪个水平能得到最大值或最小值。

由正交表可知

式中：Sj为第j列的偏差平方和。Sj值较大则表示该列所在的因子影响较大。表中B因子的Sj最大，故其对MZ的影响最大。

去掉表6中各试验号得到不同外力下叉桩桩顶的MZ、MX、FY、FX的分析如下，由于FZ、MY的数值很小，其对结构的影响也较小，故未对其进行分析。

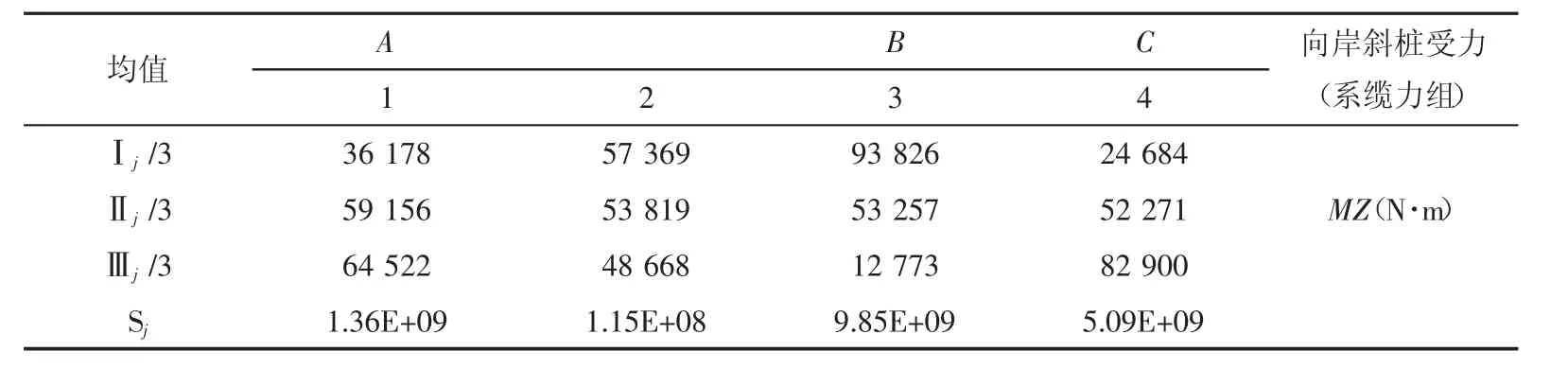
表7 系缆力作用下向岸斜桩MZ计算表格Tab.7 MZ calculation table of the inclined piles under the mooring force

由表6和表7可知：水平力（撞击力和船舶系缆力）对向岸斜桩的MZ值影响最大，其次是后承台和后方堆场的均布荷载，码头前沿的浚深和码头岸线的回淤量对MZ值的影响最小。作用于码头的水平力（撞击力、系缆力）由小到大变化时（系缆力为负），向岸斜桩的MZ递增（朝着使坐标轴正方向的面受拉方向发展）；向岸斜桩的MZ值会随着后承台及后方堆场的竖向均布荷载的增加而增加；码头的浚深和岸线回淤量的加大，也会使向岸斜桩的MZ值呈递增的趋势，但其由水平2变化到水平3时，对MZ的改变量较小。

所以向岸斜桩的MZ值在组合33（撞）3工况下达到最大值，13（拉）1下达到最小值。

向岸斜桩的FY、FX、MX以及向海斜桩的MZ、FY、FX、MX采用与前面相同的分析方法得到以下结论。

（1）向岸斜桩。对向岸斜桩FY、MX值影响最大的是撞击力和船舶系缆力，其次是后承台和后方堆场的均布荷载，码头前沿的浚深和码头岸线的回淤量对FY值的影响最小；对向岸斜桩的FX值影响最大的是后承台和后方堆场的均布荷载，其次是撞击力和船舶系缆力，码头前沿的浚深及码头岸线的回淤量对FX值的影响甚微。

作用于码头的水平力（撞击力、系缆力）由小到大变化时（系缆力为负），向岸斜桩的FY值减小（朝着使截面受压的方向发展）、FX值递增（使截面受坐标轴正方向的水平力）、MX值减小（朝着使坐标轴负方向的面受拉方向发展）；后承台及后方堆场的竖向均布荷载的增加使向岸斜桩的FY值增加、FX值增加、MX值减小；码头的浚深和岸线回淤量的增加使FY值增加（但其由水平2变化到水平3时比由水平1变化到水平2的改变量小很多）、FX值增加（但其由水平2变化到水平3时比由水平1变化到水平2的改变量小很多）、MX减小。

所以向岸斜桩的FY值在组合33（拉）3工况下达到最大值，13（撞）1下达到最小值；向岸斜桩的FX值在组合33（撞）3工况下达到最大值，13（拉）1下达到最小值；向岸斜桩的MX值在组合13（拉）1工况下达到最大值，33（撞）3下达到最小值。

（2）向海斜桩。对向海斜桩的MZ、FY、FX、MX值影响最大的是撞击力和船舶系缆力；MZ、FY、MX的次要影响因素是后承台和后方堆场的均布荷载，FX的次要影响因素是码头前沿的浚深和码头岸线的回淤量；码头前沿的浚深和码头岸线的回淤量对MZ、FY、MX影响最小，后承台和后方堆场的均布荷载对FX值的影响最小。

作用于码头的水平力（撞击力、系缆力）由小到大变化时（系缆力为负），向海斜桩的弯矩值MZ增加（朝着使坐标轴正方向的面受拉方向发展）、FY值增加、FX值增加、MX值减小；后承台及后方堆场的竖向均布荷载的增加使向海斜桩的MZ值增加、FY值减小、FX值增大、MX值减小；码头浚深和岸线回淤量的增大使向海斜桩的MZ值减小、FY值减小、FX值减小、MX值减小。

所以向海斜桩的MZ值在组合13（撞）3工况下达到最大值，33（拉）1下达到最小值；向海斜桩的FY值在组合13（撞）1工况下达到最大值，33（拉）3下达到最小值；向海斜桩的FX值在组合13（撞）3工况下达到最大值，33（拉）1下达到最小值；向海斜桩的MX在组合13（拉）1工况下达到最大值，33（撞）3下达到最小值。

4 结论

利用ANSYS有限元软件，建立了以高桩码头结构与土相互作用的数值计算模型；重点分析了在不同作用力及各水平下，高桩码头叉桩的受力（MZ、MX、FY、FX）情况，得出了以下结论：

（1）码头前沿的浚深和码头岸线的回淤量由水平2变化到水平3时，对向岸斜桩MZ、FY、FX的改变量很小，远远小于由水平1变化到水平2时的改变；其余都呈现出了较强的线性变化过程。

（2）向岸斜桩的MZ值在组合33（撞）3工况下达到最大值，13（拉）1下达到最小值；FY值在组合33（拉）3工况下达到最大值，13（撞）1下达到最小值；FX值在组合33（撞）3工况下达到最大值，13（拉）1下达到最小值；MX值在组合13（拉）1工况下达到最大值，33（撞）3下达到最小值。对向岸斜桩的MZ、FY、MX影响最大的是水平力（撞击力和船舶系缆力），对FX值影响最大的是后承台和后方堆场的均布荷载。

（3）向海斜桩的MZ值在组合13（撞）3工况下达到最大值，33（拉）1下达到最小值；FY值在组合13（撞）1工况下达到最大值，33（拉）3下达到最小值；FX值在组合13（撞）3工况下达到最大值，33（拉）1下达到最小值；MX在组合13（拉）1工况下达到最大值，33（撞）3下达到最小值。对向海斜桩的MZ、FY、FX、MX影响最大的均是水平力（撞击力和船舶系缆力）。

［1］刘现鹏，张强.天津港码头设施2009年秋季调查报告［R］.天津：天津港务局，2009.

［2］廖雄华，张克绪.天津港高桩码头桩基—岸坡土体相互作用的数值分析［J］.水利学报，2002（4）：81-87.LIAO X H，ZHANG K X.Numerical analysis of pile-soil interaction in long-piled wharf of Tianjin Port［J］.Journal of Hydraulic Engineering，2002（4）：81-87.

［3］江见鲸，陆新征，叶列平.混凝土结构有限元分析［M］.北京：清华大学出版社，2005.

［4］孔丹丹，赵颖华，王萍.仿真计算中钢筋混凝土材料的等效模量［J］.沈阳建筑工程学院学报：自然科学版，2003（3）：165-168.KONG D D，ZHAO Y H，WANG P.Equivalent moduli of reinforced concrete in simulating analysis［J］.Journal of Shenyang Architectural and Civil Engineering Institute：Natural Science Edition，2003（3）：165-168.

［5］甘立刚，李碧雄，吴体，等.桩土接触数值模拟试验［J］.四川建筑科学研究，2009（2）：131-134.

［6］许宏发，吴华杰，郭少平，等.桩土接触面单元参数分析［J］.探矿工程，2002（5）：10-12.XU H F，WU H J，GUO S P，et al.Study on the Parameters of Pile Soil Contact Surface Element［J］.Exploration Engineering，2002（5）：10-12.

［7］JTJ215-98，港口工程荷载规范［S］.

［8］吴群英.应用数理统计［M］.天津：天津大学出版社，2004.