复杂水域波浪物理模型与数学模型对比研究
刘欣明,刘海成,迟 杰
(1.河海大学,南京210024;2.交通部天津水运工程科学研究所工程泥沙交通行业重点实验室,天津300456)
与物理模型比较,数学模型存在一些固有缺点,如对于波况复杂的局部区域,同时存在波浪折射、反射绕射、破碎、爬坡等作用时,往往很难较好反映出实际物理现象。一方面,数学模型很难真实模拟建筑物的具体结构型式,仅用一个简单的透射系数来区别各种不同结构型式的建筑物;另一方面,数学模型在应用中受到许多限制,实际工程的模拟难以达到应用要求,如MIKE21-BW对于波浪破碎的模拟就严格限制了空间和时间的步长[1]。因此在工程中经常会视情况对数学模拟进行一些概化处理,忽略波浪破碎的影响或经验假设建筑物的透射系数等。本次工程数学模拟运用多种不同的概化处理方案模拟出多个结果,最后再与物理模型结果进行比较分析。
本工程位于山东半岛北侧烟台港西侧新港区内,区域面积约为1.7 km×2.4 km。工程区主要建设项目包括预制场滑道、西侧突堤工作船码头、一个5万t级液体化工泊位(LPG泊位)及相应的航道港池(航道边坡1:5)、已建 1 500 m 长的北防波堤[2](图 1)。
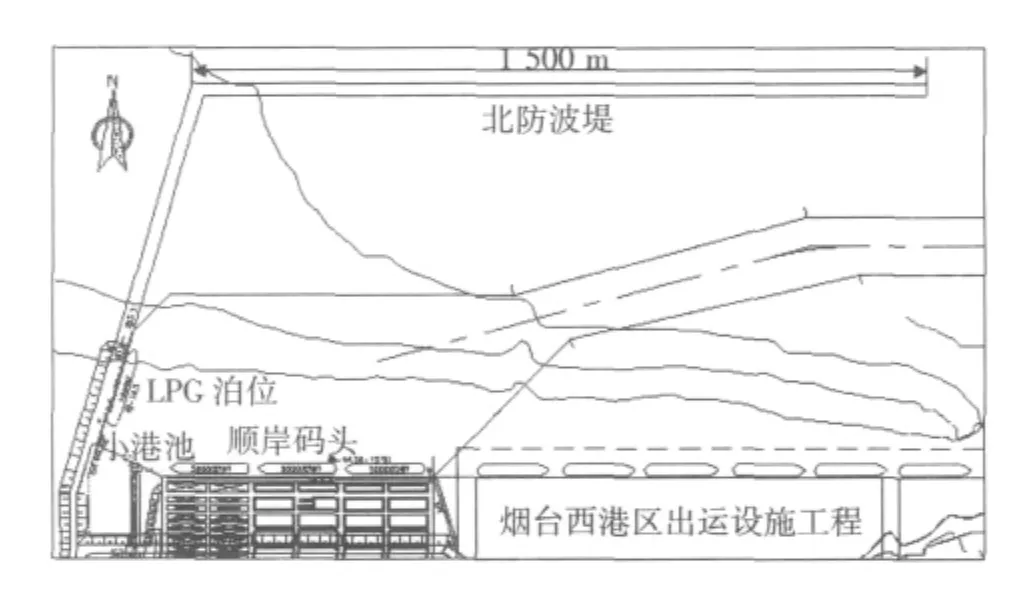
图1 工程平面图Fig.1 Plan layout of the project
1 试验基本参数
工程主要受ENE向波浪影响。根据芝罘岛海洋站的测波和测风资料、烟台西港区施工现场的风浪资料以及现场附近气象站的气象资料,推算出工程海域-15 m处ENE向不同水位的波浪要素(表1)。
试验水位包括极端高水位+3.56 m,设计高水位+2.46 m,设计低水位+0.25 m以及极端低水位-0.95 m[2]。
2 数学模型
数学模型采用丹麦水力研究所开发的数值模拟软件MIKE21中的BW模块。
2.1 MIKE21-BW模块简介
BW模块是以Boussinesq方程为基础,通过求解沿垂线积分的Boussinesq方程获得沿水深平均的流速、水位和波高等物理量[3-4],能够模拟在沿海和港区内多种波浪的组合影响,如波浪的反射、折射、衍射、破碎和长波产生等。在模拟反射时可以模拟任意反射率的反射情况,可用于研究和分析港口及沿海地区复杂的多种波浪作用组合扰动的情况。其基本表达式[4-5]如下
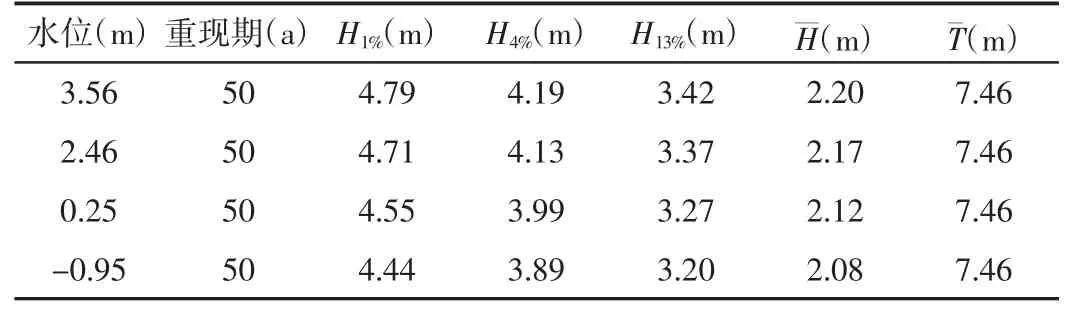
表1 ENE向不同水位试验波要素(-15 m水深处)Tab.1 Wave parameters of different water levels in ENE direction
连续性方程

x方向动量方程
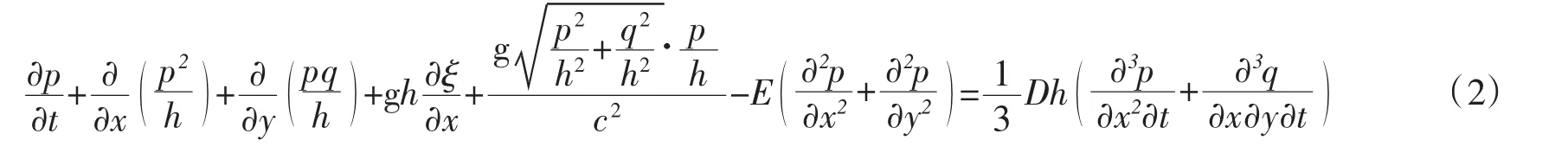
y方向动量方程
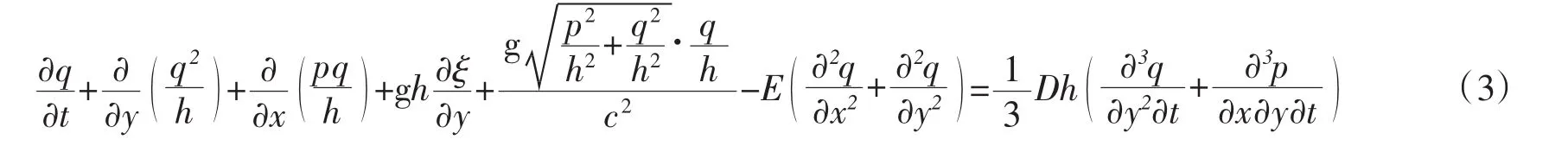
式中:x,y为水平坐标,m;t为时间,s;ξ为高出平均水位的水面高度,m;p,q 分别为 x,y方向流量密度;h 为水深,m;D为平均水深,m;c为谢才阻力系数;E为紊动“涡粘”系数;g为重力加速度。
2.2 数学模型概化处理方案
本工程的数学模拟存在以下难点:一是模拟港区的复杂波况较困难。大部分水域的波浪都是由入射波和建筑物反射波叠加而成,尤其是小港池内,四周壁岸均为直立式结构,且拐角处波浪更是经过数次反射后形成的,而且小港池滑道处还有波浪破碎、爬坡和波浪反射等现象同时存在的情况,再加上航道导致的波浪折射,大大增加了数值模拟的难度;二是模拟滑道处的波浪破碎和爬坡比较困难。BW模块虽然可以模拟破浪破碎,但在应用中有严格的限制:空间网格步长要求取得很小,一般为1~2 m;破碎处的地形要求高程变化率很小(根据BW模块给出的几个典型实例推断相邻网格间高程变化小于0.1 m为宜);为了尽量准确反映实际物理情况,且兼顾实际工程应用需求,采用以下5种概化方案进行数学模拟。
方案一,忽略滑道,忽略破碎,建筑物经验假设为全反射,网格步长△x=△y=3 m,时间步长△t=0.1 s,采用JONSWAP谱生成不规则波。这一方案主要是考虑到小港池部分仅占整个模拟区域的5%左右,因此简化其地形,进而忽略此处滑道以及其上的波浪破碎和爬坡。建筑物多为直立式结构,从以往数学模拟经验来看,将其设为透射率为0.99的全反射层比较合适[6]。
方案二,按实际坡度设置滑道,忽略破碎,建筑物假设为全反射,网格步长△x=△y=3 m,时间步长△t=0.1 s,采用JONSWAP谱生成不规则波。由于滑道水深较浅且露出水面处会导致计算溢出,遂把此处地形处理成全反射建筑物,其他建筑物反射率不变。
方案三,按实际坡度设置滑道,忽略破碎,建筑物假设为全反射,滑道水深较浅和露出水面处设为半反射建筑物,网格步长△x=△y=3 m,时间步长△t=0.1 s,采用JONSWAP谱生成不规则波。改变建筑物透射率也是数学模拟中常用处理手段,故此处滑道概化处理所产生的假想建筑物宜采用不同透射率来模拟,使之接近实际情况。
方案四,按实际坡度设置滑道,增加破碎项,建筑物假设为全反射,网格步长△x=△y=2m,时间步长△t=0.1 s,采用JONSWAP谱生成不规则波。滑道露出水面处设置为全反射建筑物。
方案五,按实际坡度设置滑道,忽略破碎,建筑物假设为全反射,滑道露出水面处设置为半反射建筑物网格步长△x=△y=2 m,时间步长△t=0.1 s,采用JONSWAP谱生成不规则波。
3 物理模型设计与制作
模型按重力相似准则设计,取几何比尺为1∶100,水深比尺、波高比尺、波长比尺也为1:100,波浪周期比尺为1:10。模型采用桩点法复制,平面尺寸及高程按几何相似原则制作,根据试验要求布置测波点。试验区包括原工程码头、LPG泊位、顺岸码头、防波堤、港池水域、航道及护岸。其中港池航道底高程-14.0 m,码头及防波堤顶高程+5.5 m,防波堤胸墙顶高程+9.5 m。模型波浪由摇板式不规则波造波机产生。模型波高用SG2008型动态波高测量系统自动采集[2]。
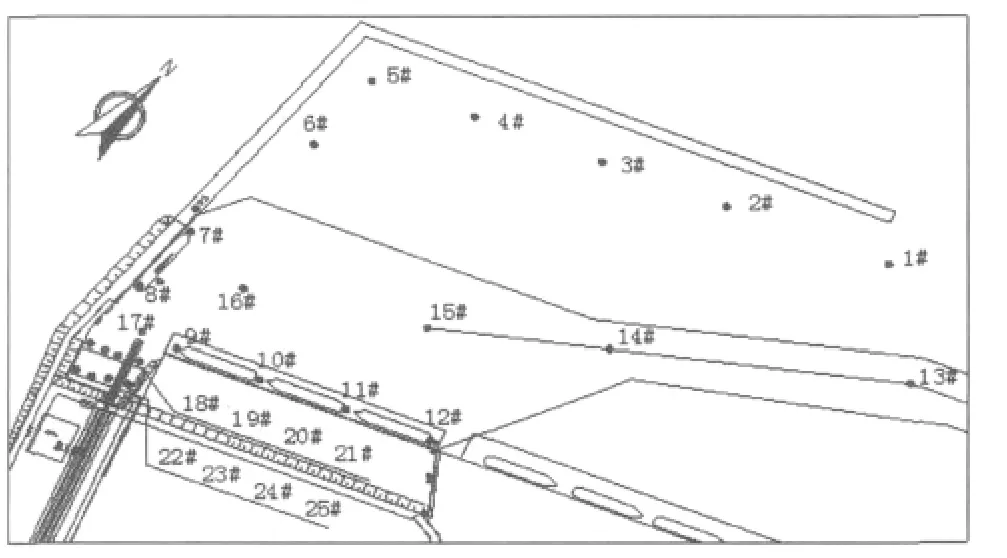
图2 测点布置图Fig.2 Location of measuring points
4 试验结果对比研究[7-8]
4.1 大港池波高分布分析
设计高水位下,大港池物理模型各测点波高值与数学模型结果对比情况见表2。由表2可以看出,大港池内各个数学模型方案的波高分布与物理模型试验结果吻合较好。
北侧防波堤波高从东向西逐渐减小,直至西侧堤前转为沿堤逐渐增大,此逐渐增大的波浪经过LPG码头,一直延续到小港池内,形成类似沿防波堤传播的较大波浪,实际上这是由北侧直立式防波堤、南侧顺岸码头、西侧防波堤本身反射的波浪与外海传入波浪相互叠加产生的马赫效应波浪。这一复杂现象在数学模型中反映的比较好,且波高数值也基本一致,误差均在10%左右。
顺岸码头处,岸壁为直立式结构,此处波浪反射作用也很明显,尤其是西侧拐角处,同时存在LPG泊位反射波浪和小港池内反射波浪,并伴随有一定波浪绕射,导致波高较大,码头上水明显。数学模型模拟结果中,此处波高值均偏小。总体来看,无论是波高由东向西沿岸逐渐减小的趋势,还是波高数值,都与物理模型试验结果基本相似。
航道处4个点的数值模拟结果与物理模型的结果差距较大,虽然波高分布情况大致相同,但其趋势并不明显,4个点数值很接近。15#点的波高值比物理模型试验结果小了近20%,这说明BW模块对计算波浪折射叠加多次反射波浪的复合情况存在较大误差,这也可能是地形原因造成的,航道边坡坡度比较小,相对于BW计算要求来说过陡。
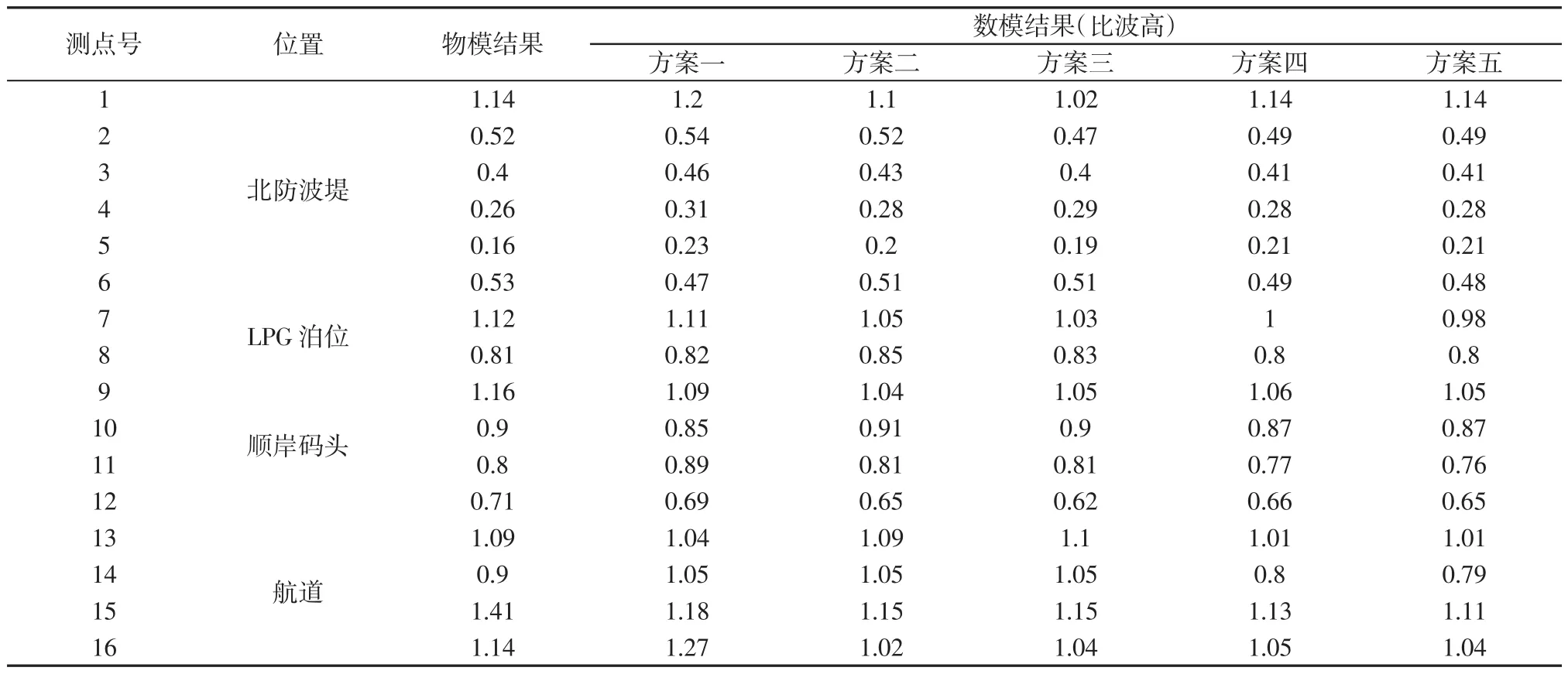
表2 设计高水位大港池数学模型与物理模型波高结果Tab.2 Wave heights of design high-water level in large harbor basin by mathematical model and physical model test
对比各个方案,由于仅仅改变小港池滑道处地形和折射率,对大港池区域影响不大,只有方案一16#点处波高值略大,这是方案一省略了滑道,小港池的波浪直接反射到此处的缘故。
4.2 小港池波高分布分析
由图3中数学模型结果与物理模型结果对比可以看出,小港池内各方案波高变化趋势基本与物理模型一致,但其数值上有较大差距。22#测点处各方案波高值比物理模型小很多,此测点位于小港池西侧拐角处,波浪作用复杂,同时存在北侧防波提、小港池东侧、西侧直立壁岸反射的波浪,ENE向入射波浪,顺岸码头拐角处绕射波以及沿西防波堤传播过来的波浪,波能强烈集中,而数值模拟不能很好地反映这一波高变化过程。24#测点为滑道水陆交界点,波浪破碎爬坡现象明显,波能消耗较大,方案一由于忽略了滑道且不考虑破碎,故此处波高数值较其他方案和物理模型大很多。比较方案二与方案四,同时比较方案三与方案五,发现增加破碎项并没有对小港池波高产生明显影响,仅在22#、23#测点处波高略有减小,且比物理模型结果要小。再将2个仅滑道处反射率不同的方案(方案二与方案三,方案四与方案五)进行比较,可以看出反射率的改变对小港池数值几乎没有影响。
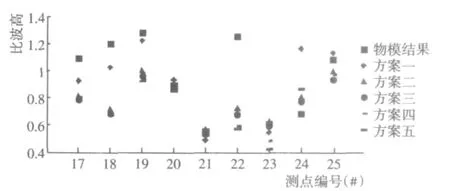
图3 设计高水位小港池数学模型与物理模型波高结果Fig.3 Wave heights of design high-water level in small harbor basin by mathematical model and physical model test
5 结论及展望
(1)在ENE向波浪作用下,进入大港池波浪在北侧、西侧防波堤和顺岸码头处均有较强烈反射,且相互叠加,并在西侧防波堤处产生波浪沿堤传播的马赫效应。物理模型和数学模型模拟结果基本吻合,皆能较好反映港池内外波高分布。
(2)进入小港池的波浪多为北侧和西侧防波堤、LPG泊位的反射波和顺岸码头的绕射波,经过在小港池内进一步反射和叠加,在西侧和东侧岸壁处产生较大波浪,其中西侧拐角处波能集中最明显。数学模型虽然可以大致模拟出波浪变化趋势,但波高数值与物理模型相比相去甚远,并未在西侧岸壁和拐角处形成较大波能集中,整体波高数值偏小。
(3)对比5个数学模型方案,方案一波高分布与物理模型最为接近,可作为研究本工程波高分布情况的参考。若重点研究小港池波况,数值模拟结果均不理想,可见对于小尺度局部区域且波浪大部分伴有破碎和爬高的反射绕射波的情况,MIKE21-BW模块模拟效果仍旧不够理想。
(4)由方案二、三、四、五可以看出,在仅有局部区域存在破碎的情况下,增加破碎项以及改变破碎区建筑物透射系数并不会对数值模拟结果产生明显影响,也无助于提高其准确程度,故引申本工程情况可以认为,当破碎区域尺度过小,不大于整体区域面积5%的情况下,完全可以忽略破碎对波高分布的影响。
(5)对比2 m网格(方案四、五)与3 m网格(方案二、三)的数值模拟结果,网格尺度在允许范围内的改变对计算结果没有显著的影响。由表2数据可以看出,地形相同、网格尺度相同的情况下,较小网格的2次计算结果偏差较小,所以为了避免计算随机误差,建议在可接受的时间范围内选用较小的网格计算。
考虑到数学模型的缺点,且为了节省计算时间,往往对数学模型进行一些必要的概化处理,但关于概化处理的研究却很少,多数情况下都是基于经验带有主观随意性的对数学模型进行概化处理,希望今后加强这方面的研究,使得数值模拟更规范,结果更可信。
[1]刘针,陈汉宝,张慈珩.小面积掩护水域波浪物理模型与数学模型对比研究[J].水道港口,2009,30(4):241-245.LIU Z,CHEN H B,ZHANG C H.Comparison study between numerical model and experiment test on wave in limited sheltered waters[J].Journal of Waterway and Harbor,2009,30(4):241-245.
[2]刘海成.烟台港西港区出运设施工程波浪物理模型试验报告[R].天津:交通部天津水运工程科学研究所,2009.
[3]陈雪峰,王桂萱.MIKE21计算软件及其在长兴岛海域改造工程上的应用[J].大连大学学报,2007,28(6):93-98.CHEN X F,WANG G X.MIKE 21 Software and its Application on the Offshore Reconstruction Engineering of Changxing Islands[J].Journal of Dalian University,2007,28(6):93-98.
[4]DHI Software.MIKE21 Boussinesq Wave Model User Guide[M].Danmark:DHI Software,2005.
[5]李春颖,李绍武.基于 Boussinesq 方程的波浪破碎模型的研究综述[J].港工技术,2003(4):1-4.LI C Y,LI S W.A Review of Boussinesq-type Equations and Breaking Models[J].Port Engineering Technology,2003(4):1-4.
[6]顾立忠,关琨,郑国栋.浅谈 MIKE21 模型地形前处理技巧[J].广东水利水电,2008(8):122-124.
[7]刘海源,张慈珩.三亚南山港波浪数模与物模试验对比研究[J].水道港口,2006,27(4):231-235.LIU H Y,ZHANG C H.Comparison study between mathematical and physical model tests on waves in Nanshan Harbor in Sanya[J].Journal of Waterway and Harbor,2006,27(4):231-235.
[8]张娜,郭科,王旭辉.MIKE21-BW模型在日照港总平面设计方案可行性研究中的应用[J].中国港湾建设,2007(1):32-34.ZHANG N,GUO K,WANG X H.Application of MIKE21-BW Model to Feasibility Study of General Plan Layout of Rizhao Port[J].China Harbour Engineering,2007(1):32-34.

