高压相BeO晶体的电子结构和光学性质

刘小良 任 意 梁亮文 徐 慧

(1中南大学物理科学与技术学院,长沙 410083;2中南大学冶金科学与工程学院,长沙 410083)

高压相BeO晶体的电子结构和光学性质

刘小良1,2,*任 意1梁亮文1徐 慧1

(1中南大学物理科学与技术学院,长沙 410083;2中南大学冶金科学与工程学院,长沙 410083)

应用基于密度泛函理论的第一性原理研究方法,考虑广义梯度近似(GGA)下的交换关联势,模拟计算了高压下纤维锌矿(WZ)、闪锌矿(ZB)和岩盐(RS)结构氧化铍(BeO)晶体的电子结构和光学性质等.计算结果表明,随着压力的增加,同种结构下原子间的键长和电荷转移有所减小,并且价带和导带分别向低能和高能方向移动,禁带展宽.与常压下的BeO相比,随着压力的增加,三种结构的BeO晶体的光学性质有一定的变化,介电函数、吸收系数、折射率以及电子能量损失谱曲线出现更多的精细结构,峰的数量增多;各高压相结构的吸收谱和能量损失谱宽度逐次展宽;吸收系数曲线的吸收峰及其位于低能区域的吸收边以及电子能量损失谱峰的位置均发生一定程度的蓝移.

密度泛函理论;BeO;电子结构;光学性质

氧化铍(BeO)为II-VI族直接带隙氧化物,在常温常压下呈六方纤维锌矿结构.它的硬度非常高[1],具有较高的热导率、熔点和电阻率[2],在工业上可用于催化剂、半导体器件等[3].此外,作为一种宽带隙、紫外光透明的氧化物,BeO在平板显示器以及太阳能电池方面有着广阔的应用前景[4].近年来,人们对BeO进行了广泛的研究:van Camp[5]、Boettger[6]等分别用局域密度近似和全势能线性Muffin-Tin轨道组合(FP-LMTO)方法研究了基态BeO的结构性质,他们的结果表明常温常压下BeO的构型为六方纤维锌矿结构;Chang等[7]用局域密度近似、广义梯度近似和Hatree-Fock方法[8]计算了BeO晶体的电子结构;在相变方面,Park[9]、van Camp等[5]预测在高压下BeO将依次经历纤维锌矿结构(WZ)→闪锌矿结构(ZB)→岩盐(RS)结构的相变.由于使用了不同的计算方法和交换关联势,他们报道的相变压力仍然存在分歧.鉴于广义梯度近似(GGA)在预测相变压力方面比局域密度近似(LDA)更有效[9-10],本文在后续计算中采用文献[9]报道的相变压力(由GGA方法得出).在光学性质方面,Bouhalouane等[3]计算了常压下基态和激发态BeO晶体的介电函数和电子能量损失谱,Groh等[4]发现常压下WZ、ZB、RS结构BeO晶体的光学性质几乎相同.我们知道,压力作用下材料的某些性质可能发生变化,例如Wang等[11]发现一定压力下ZnO晶体呈现出一些有趣的光学性质,因此,了解这些变化有助于挖掘材料的应用潜能.但据我们所知,一定压力下BeO晶体的电学性质和光学性质还鲜见报道.本文针对高压相BeO晶体,运用第一性原理的方法计算91 GPa(文献[9]报道的由WZ结构到ZB结构相变压力)静压下WZ、ZB结构以及147 GPa(文献[9]报道的由ZB结构到RS结构相变压力)静压下ZB、RS结构BeO晶体的电学和光学性质,并将它们与0 GPa下WZ结构BeO晶体的相应性质做比较.由于光学性质依赖于电子的带内和带间跃迁,首先对BeO晶体进行结构优化并研究电子结构,然后系统讨论BeO晶体的光学性质,包括介电函数、吸收系数和能量损失谱等.

1 模型和方法

本文讨论的晶体结构模型如图1所示,图中(ac)分别表示WZ、ZB和RS结构的BeO晶胞.WZ结构属于P63mc空间群,计算中采用的晶格参数初始值为a=b=0.2698 nm,c=0.4380 nm,α=β=90°,γ= 120°,内坐标u=0.378[1];ZB结构所属空间群为F43m,计算中采用的晶格参数的初始值为a=b=c= 0.3726 nm,α=β=γ=90°[3];RS结构所属的空间群为Fm3M,计算中采用的晶格参数的初始值为a=b=c= 0.3571 nm,α=β=γ=90°[9].

本文所有计算均由 Materials Studio中的CASTEP[12-14]模块完成,它被广泛用于计算材料的电子结构[15-17]及光学性质[18-19]等.首先用CASTEP模块中的BFGS算法在上文所述的压力下对三种晶体进行结构优化.由于在预测相变压力方面GGA比LDA更加有效[10],计算中的交换关联势采用GGA下的 Perdew-Burke-Eruzerhof(PBE)方案[20],并用超软势(USP)[21]描述离子实与价电子之间的相互作用势.

为确保所做计算的收敛性,首先考察平面波截断能以及k网格大小设置对晶体总能量的影响.以纤维锌矿BeO晶体为例,总能量随截断能和k网格大小的变化在图2(a)和图2(b)中分别给出.

可以看出,在k网格大小固定为12×12×8的条件下,当截断能高于550 eV时,总能量的变化不超过1.6 meV·atom-1,另一方面,在截断能设置为550 eV的条件下,当k网格的设置大于8×8×5时,总能量的收敛性已经非常好了.根据收敛性检测的结果,将平面波截断能设置为750 eV.k网格大小的设置如下:对WZ结构BeO,k网格取12×12×8;对ZB结构BeO,k网格取13×13×13;对RS结构BeO,k网格取10×10×9.

为得到晶体的能带结构和电子态密度分布,利用自洽迭代方法求解Kohn-Shame方程

图1 BeO的晶胞Fig.1 Crystal cells of BeO(a)WZ structure;(b)ZB structure;(c)RS structure

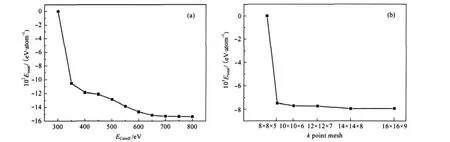
图2 不同计算参数下WZ BeO晶胞总能量的收敛情况Fig.2 Convergences of the total energy of WZ BeO at different computational parameters(a)total energy versus the cutoff energy for the k point mesh of 12×12×8,(b)total energy versus the k point mesh set for the cutoff energy of 550 eV

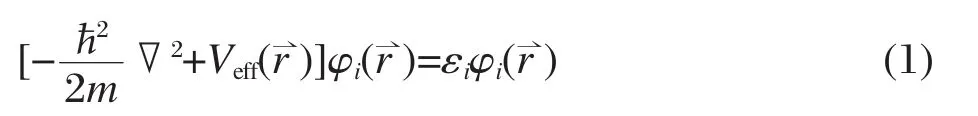
晶体的光学特性可由偶极跃迁矩阵元获得,其介电函数ε(ω)=ε1(ω)+iε2(ω)的虚部ε2(ω)满足关系式:

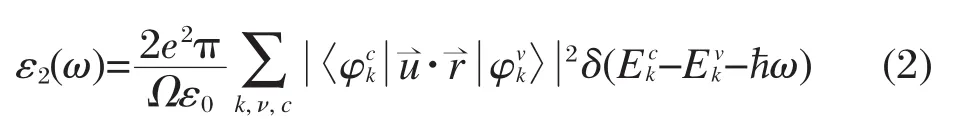
其中e为电子电量,Ω为正格子原胞体积,ε0为真空中的介电常数,求和指标k、ν、c分别表示布里渊区中的点、价带中的能级、导带中的能级,为导带(价带)中与布里渊区k点相对应的电子态函数,为相应能级的能量,为入射场的极化矢量,为极化方向的单位矢,ω为入射场的频率,ħ为约化普朗克常数.至于介电函数的实部,可由Kramers-变换得到,

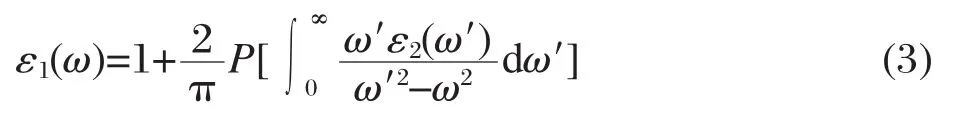
其中P为柯西积分的主值.

晶体的能量损失谱L(ω)[22-23]和吸收系数直接由介电函数得出

其中c为真空中的光速.

2 结果和讨论

2.1 晶格参数和布居分析

为了获得BeO的晶格参数,我们对不同压力下的WZ、ZB和RS结构的BeO晶胞进行了几何结构优化.按照晶胞能量与体积关系的最小化原理得到的晶格参数如表1所示,实验[1]和其他理论方法[4-6,24]获得的WZ结构的BeO晶格结构参数值也在表1中给出以供比较.可以看出,同种结构下的晶格常数随压力增大而减小.对于0 GPa下的WZ结构BeO,经过优化后得到的a、c/a以及u,与实验结果和其他理论计算取得的结果符合较好.对于0 GPa下ZB和RS相的BeO,优化后的晶格参数和其他理论计算取得的结果符合得很好.

除晶格结构参数外,还计算了不同压力下WZ、ZB和RS相的BeO晶体中的原子间的电荷转移、重叠布居数以及键长,所得结果与晶格结构参数一同列于表1.虽然由布居分析[25-26]获得的原子之间的电荷转移的绝对数值没有多大的物理意义,但仍然可以通过比较它们的相对数值获得一些有用的信息.而重叠布居表示两成键原子的电子云的重叠程度,可以用来衡量两原子之间所成键的离子性或共价性的强弱.较小重叠布居数表明两原子所成键离子性较强;较大的布居数表明两原子间形成较强的共价键;重叠布居数为零,表明两原子间没有明显的成键.

表1显示原子间的电荷转移和键长随着压力的增加而减少,键布居值随压力的增大而增大.对于WZ结构的BeO,当压力从0增加到91 GPa时,电荷转移从0.76e减小到0.72e,Be—O键长从0.1672 nm减小到0.1529 nm,但重叠布居值由0.725增大为0.820.对于ZB结构的BeO,当压力从0 GPa增加到91 GPa时,电荷转移从0.75e减小到0.71e, Be—O键长从0.1673 nm减小到0.1529 nm,重叠布居值由0.420增大为0.445;当压力从91 GPa增加到147 GPa时,电荷转移从 0.71e减小到 0.69e, Be—O键长从0.1529 nm减小到0.1481 nm,重叠布居值由0.445增大为0.453.对于RS结构的BeO,当压力从0增加到147 GPa时,电荷转移从0.74e减小到 0.68e,Be—O键长从 0.1841 nm减小到0.1652 nm,重叠布居值由0.395增大为0.425.静压力下电荷转移减少以及键布居值的增加,表明压力使三种结构的BeO的离子性减弱,共价性增强.这些变化将会影响BeO晶体的电子能带结构和态密度,进而影响晶体的光学性质.

表1 相应相变压力下各种结构的BeO晶体结构参数、键长、键布居值和原子间电荷转移Table 1 Lattice parameters,bond length,bond population and charge transfers of WZ,ZB and RS phase BeO under different structure phase transition pressures

2.2 电子结构

用广义梯度近似计算的不同压力下的WZ、ZB和RS结构的BeO带隙宽度在表2中列出.

对于0 GPa下WZ结构BeO,带隙宽度的实验数值[27]和其他的理论计算值[4,28]一并在表2中给出.对于0 GPa下WZ结构BeO,本文计算获得的禁带宽度为7.33 eV,与实验值10.6 eV相比,偏小约30%.但本文计算结果与其他文献报道的理论计算值基本符合.对于0 GPa下ZB、RS结构BeO,本文计算的禁带宽度分别为7.27、7.99 eV,Groh等[4]用全电子密度泛函方法计算ZB和RS结构BeO的带隙分别为10.79和10.96 eV.

为方便后面讨论光学性质,用剪刀算子对带隙宽度进行修正.对WZ结构,剪刀算子值取为3.27 eV,对ZB和RS结构,剪刀算子分别取为3.52和2.97 eV(鉴于Groh等[4]用全电子密度泛函方法能较准确计算BeO的带隙,这里以文献[4]报道的ZB和RS结构BeO的带隙作参照取剪刀算子对ZB和RS结构BeO带隙进行修正).图3和图4分别给出了修正后不同压力下三种结构BeO晶体的电子能带结构和态密度,图中虚线表示费米面的位置.

图3为不同压力下WZ、ZB和RS结构的能带结构.由图3可知,对于三种结构,随着压力的增加,导带下部能级向高能方向移动,同时价带有向低能方向移动的趋势,能级的移动使带隙变宽.由图3清楚地看到压力对导带最低点的位置的影响.0 GPa下WZ和RS结构导带最低点位于Γ点,属直接型带隙,ZB结构导带最低点位于W点,属间接型带隙(此时导带底部W和Γ点所对应的能量相差不大).在91 GPa下,WZ结构导带最低点位于K点;147 GPa下RS结构导带最低点位于L点附近;91 GPa和147 GPa压力下ZB结构的导带最低点仍位于W点,但导带底部W点和Γ点所对应的能量相差较大.图4为不同压力下O原子和Be原子的电子分态密度.图中导带下部态密度主要来自Be 2s电子的贡献,价带下部态密度主要来自O 2s电子,价带上部态密度来自于O 2p电子的贡献.现以WZ结构的电子态密度为例分析压力对电子性质的影响.当压力由0 GPa增加到91 GPa时,O 2s态密度的峰值位置由-16.22 eV移至-17.08 eV,O 2p态密度的主峰位置由-1.31 eV移至-1.78 eV,Be 2s态密度曲线最接近导带底的峰值位置由12.72 eV移至14.46 eV.除态密度主峰位置的变化外,压力还使态密度展宽,态密度发生峰劈裂.

表2 不同结构相变压力下WZ、ZB和RS相BeO晶体的带隙宽度Table 2 Energy band gaps of WZ,ZB and RS phase BeO under different structure phase transition pressures

图3 不同压力下WZ、ZB和RS结构的能带结构Fig.3 Band structures of WZ,ZB and RS structures under different pressures

2.3 光学性质

图4 不同压力下WZ、ZB和RS结构的Be 2s、O 2s和O 2p电子分态密度Fig.4 Partial density of states for Be 2s,O 2s and O 2p of WZ,ZB,and RS BeO under different pressures

为方便比较,下面涉及到的光学性质均为BeO多晶体的情形.利用介电函数与跃迁矩阵之间的关系式(2)和Kramers-Krönig变换式(3),可得到不同压力下多晶态的WZ、ZB和RS结构BeO的介电函数ε(ω),见图5,其中实线表示介电函数的实部ε1(ω),虚线表示介电函数的虚部ε2(ω).

由于介电函数的虚部ε2(ω)沟通了微观电子结构和宏观光学性质,这里主要讨论介电函数的虚部ε2(ω).在0 GPa下,WZ结构的介电函数的虚部ε2(ω)有五个较明显的峰,分别位于10.6、11.8、13.4、14.6、17.6、18.4 eV处.这些峰分别对应电子在价带顶部与Γ、L、M、H、A、Γ(费米面以上第八能级)点之间的跃迁.ZB结构介电函数的虚部ε2(ω)的峰位置为10.8、12.5、17.5、20.5、24 eV,这些峰分别对应电子在价带顶部与导带底部Γ、K、Γ(费米面以上第二三能级)、X、W点之间的跃迁.对于RS结构,ε2(ω)的峰位置为10.8、11.9、15.5、18 eV,分别对应电子在价带顶部与L、M、Γ、K(费米面以上第四能级)点之间的跃迁.对于常压下三种结构的BeO晶体,本文得到的介电函数虚部峰的位置与文献[3]以及文献[4]的报道还存在不一致的地方.但本文所得的三种结构的介电函数虚部第一个峰的位置比较接近他们各自的禁带宽度,从这一点上看,本文结果优于文献[3-4]报道的结果.

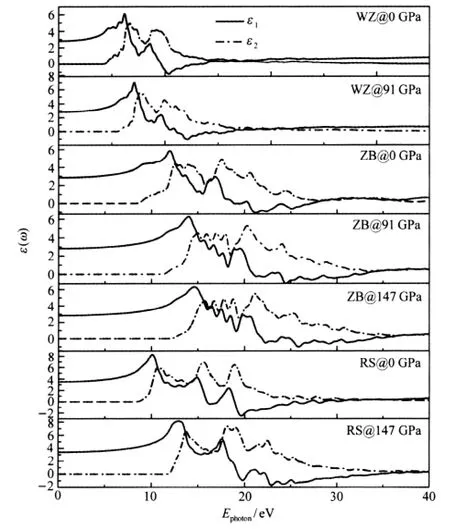
图5 不同结构相变压力下WZ,ZB和RS结构BeO的介电函数ε(ω)Fig.5 Dielectric functions ε(ω)of WZ,ZB,and RS BeO under different structure phase transitions pressures

当三种结构的晶体处在压力下时,介电函数的峰位置会向高能方向移动.例如,当静压力从0 GPa增大到91 GPa时,WZ结构的介电函数的虚部ε2(ω)峰的位置出现在12.6、15.3、16.6、19.8、21.9、23.4 eV附近.静压力作用下BeO晶体的介电函数虚部峰位置的移动现象可以从静压力下BeO晶体的电子结构的变化得到解释.从能带结构图(图3)可以发现,压力使得导带下部部分能级向高能方向移动.与常压下相比,91 GPa下WZ结构的导带底部最低点移至K点,禁带宽度变宽约2.0 eV;91 GPa和147 GPa静压力下ZB结构的导带底部最低点位于X点,禁带宽度分别变宽0.15和0.25 eV;147 GPa下RS结构的禁带变宽2.8 eV.从电子态密度图(图4)也可以清晰地看出,静压力使Be 2s电子的态密度峰的位置向高能方向移动而使得禁带变宽.由于禁带变宽,电子由价带跃迁至导带需要更多的能量,这在介电函数上表现为虚部峰的位置蓝移.此外,静压力使Be 2s电子态密度展宽,同时态密度峰发生劈裂,导致这部分电子的定域性减弱.从能带结构图中可以看到在压力作用下布里渊区高对称方向上的一些能级简并现象被消除.导带下部电子态密度展宽,态密度峰的劈裂以及布里渊区能级简并现象的消除使得静压力下同种结构的BeO的介电函数比常压下的介电函数拥有更加丰富的结构,呈现更多的峰.例如当静压力从0 GPa增大到147 GPa时,RS的介电函数虚部ε2(ω)位于15.5 eV分裂成两个峰,并且两个峰分别移至18.0、19.2 eV处.

图6(a)和6(b)分别给出了不同压力下WZ、ZB和RS结构BeO多晶的光学吸收谱和电子能量损失谱.

从图6(a)可以看出,在低能区域,三种结构的BeO对光的吸收率为零,这是因为低能区域的光子能量小于禁带宽度,不能使电子发生跃迁;而在高能区域,吸收率随着光子能量的增加而减少并逐渐趋向于零,这是因为电子难以响应高频率的光子.对比同一结构不同压力下的吸收谱可以发现,随着压力的增加吸收谱宽度逐次展宽,位于低能区域的吸收边以及各吸收谱峰的位置逐次发生蓝移.以ZB结构的BeO为例,0 GPa下吸收主峰位于21.3 eV, 91 GPa下吸收主峰位于24.3 eV处,147 GPa时吸收主峰移至25.7 eV处.此外,从整体上看,随压力的增加,各吸收谱在蓝移的同时,吸收系数有逐次增大的趋势,并且吸收谱呈现出更多的峰.从图3和图4中可发现,压力作用使三种结构的BeO的价带上移、带隙变宽,电子从价带跃迁至导带须吸收频率更高的光子.这使得整个吸收谱的位置向高能方向移动.此外,吸收峰的强弱由偶极跃迁矩阵元、价带和导带的联合态密度决定,并受选择定则制约.分别比较图4中的(a)和(b),(c)和(d)、(e)以及(f)和(g),可以发现压力使态密度的分布发生变化,导带下部态密展宽并且态密度的峰发生分裂.这种变化使得态密度分布更加符合选择定则,吸收系数更大.

图6 不同压力下三种结构的光吸收系数η(ω)和电子能量损失函数L(ω)Fig.6 Optical absorption coefficient η(ω)and electron energy-loss function L(ω)of three structures under different pressures

电子能量损失函数L(ω)是反应光学性质的一个重要参量,它描述了在材料中运动的快电子能量的损失情况.图6(b)展示了不同压力下WZ、ZB和RS结构BeO晶体的电子能量损失谱.可以发现,随着压力的增加,能量损失谱曲线在逐渐展宽的同时有整体向高能方向移动的趋势.在常压时,WZ结构BeO晶体的电子能量损失谱主峰位置为28.1 eV,与文献[3]结果一致;91 GPa时WZ结构和ZB结构的主峰值位置移至33.6 eV.当压力由0 GPa依次增加到91、147 GPa时,RS结构的能量损失谱主峰位置由27.7 eV依次移至33.6、35.3 eV.0 G和147 GPa时RS结构的峰值位置分别位于28.7、34.6 eV.

3 结论

运用密度泛函赝势方法研究了相变压力下的WZ、ZB和RS结构BeO的晶体电子结构和光学性质,计算了以上三种晶体的电子态密度、键布居数和原子间的电荷转移等电子结构参数以及介电函数、折射率、吸收系数和能量损失谱等光学参数.结果表明:(1)随着压力增加,BeO晶体内原子间的电荷重新分布,Be—O键布居值增大,Be—O键共价性增强;(2)各高压相BeO晶体的导带向高能方向移动,禁带逐次展宽;(3)随着压力的增加各高压相BeO晶体的介电函数、吸收系数、以及电子能量损失谱曲线出现更多的精细结构,峰的数量增多;(4)各高压相结构的吸收谱和能量损失谱宽度逐次展宽,吸收系数曲线的吸收峰及其位于低能区域的吸收边以及电子能量损失谱峰的位置均发生一定程度的蓝移.

1 Hazen,R.M.;Finger,L.W.J.Appl.Phys.,1986,59:3728

2 Slack,G.A.;Austerman S.B.J.Appl.Phys.,1971,42:4713

3 Bouhalouane,A.;Fouad,E.;Haj,H.J.Phys.-Condens.Matter, 2007,19:436216

4 Groh,D.;Pandey,R.;Sahariah,M.B.;Amzallag,E.;Baraille,I.; Rérat,M.J.Phys.Chem.Solids,2009,70:789

5 van Camp,P.E.;van Doren,V.E.J.Phys.-Condens.Matter,1996, 8:3385

6 Boettger,J.C.;Wills,J.M.Phys.Rev.B,1996,54:8965

7 Chang,K.J.;Froyen,S.;Cohen,M.L.J.Phys.C-Solid State Phys.,1983,16:3475

8 Soulé de Bas,B.;Dorsett,H.E.;Ford,M.J.J.Phys.Chem.Solids, 2003,64:495

9 Park,C.J.;Lee,S.G.;Ko,Y.J.;Chang,K.J.Phys.Rev.B,1999, 59:13501

10 Jaffe,J.E.;Snyder,J.A.;Lin,Z.;Hess,A.C.Phys.Rev.B,2000, 62:1660

11 Jian,S.;Wang,H.T.Phys.Rev.B,2005,71:125132

12 Segall,M.;Lindan,P.;Probert,M.;Pickard,C.;Hasnip,P.;Clark, S.;Payne,M.J.Phys.-Condens.Matter,2002,14:2717

13 Nie,Y.Z.;Xie,Y.Q.Phys.Rev.B,2007,75:174117

14 Troullier,N.;Martins,J.L.Phys.Rev.B,1991,43:1993

15 Keiji,W.;Masatoshi,S.;Hideaki,T.Electrochemistry,2001,69: 407

16 Keiji,W.;Masatoshi,S.;Hideaki T.J.Electroanal Chem.,1999, 473:250

17 Chen,K.;Fan,G.H.;Zhang,Y.;Ding,S.F.Acta Phys.-Chim.Sin., 2008,24:61 [陈 琨,范广涵,章 勇,丁少锋.物理化学学报, 2008,24:61]

18 Zhang,Z.Y.;Yang,D.L.;Liu,Y.H.;Cao,H.B.;Shao,J.X.;Jing, Q.Acta Phys.-Chim.Sin.,2009,25:1731 [张子英,杨德林,刘云虎,曹海滨,邵建新,井 群.物理化学学报,2009,25:1731]

19 Shi,L.B.;Li,R.B.;Cheng,S.;Li,M.B.Acta Phys.Sin.,2009, 58:6446 [史力斌,李容兵,成 爽,李明标.物理学报,2009, 58:6446]

20 Vanderbilt,D.Phys.Rev.B,1990,41:7892

21 Perdew,J.P.;Burke,K.;Emzerhof,M.Phys.Rev.Lett.,1996,77: 3865

22 Guan,L.;Li,Q.;Zhao,Q.X.;Guo,J.X.;Zhou,Y.;Jin,L.T.; Geng,B.;Liu,B.T.Acta Phys.Sin.,2008,57:5626 [关 丽,李 强,赵庆勋,郭建新,周 阳,金利涛,耿 波,刘保亭.物理学报,2009,57:5626]

23 Chen,K.;Fan,G.H.;Zhang,Y.Acta Phys.Sin.,2008,57:1053 [陈 琨,范广涵,章 勇.物理学报,2008,57:1053]

24 Bai,R.Y.;Jun,W.Y.;Hua,Z.G.;Guang,F.J.;Chen,X.R. Physica B,2009,404:1940

25 Segall,M.D.;Shah,R.;Pickard,C.J.;Payne,M.C.Phys.Rev.B, 1996,54:16317

26 Portal,D.S.;Artacho,E.;Soler,J.M.Solid State Commun.,1995, 95:685

27 Weber,M.J.Handbook of laser science and technology.Vol.3. Cleveland:CRC,1986

28 Baumeier,B.;Krüger,P.;Pollmann,J.Phys.Rev.B,2007,75: 045323

January 14,2010;Revised:March 26,2010;Published on Web:June 30,2010.

Electronic Structures and Optical Properties of BeO under High Pressure

LIU Xiao-Liang1,2,*REN Yi1LIANG Liang-Wen1XU Hui1
(1College of Physics Science and Technology,Central South University,Changsha 410083,P.R.China;2School of Metallurgical Science and Engineering,Central South University,Changsha 410083,P.R.China)

Density functional theory within the generalized gradient approximation(GGA)was used to investigate the electronic structures and optical properties of the BeO crystal in wurtzite(WZ),zinc blende(ZB),and rocksalt(RS)phases under high pressure.Results indicated that with an increase in pressure for all three structures,the BeO bond became shorter,the charge transfer decreased,the conduction band shifted to higher energy and consequently the width of bandgap became wider.Compared to BeO at 0 GPa,the curves of the dielectric functions,absorption coefficients,and electron energy-loss functions of the three high pressure phases showed finer structures.With an increase in pressure, the absorption coefficient spectra and the energy-loss functions expanded while the absorption edges and the absorption peaks of the absorption curves as well as the peaks of the energy-loss functions showed a blue shift to some extent.

Density functional theory; BeO; Electronic structure; Optical property

[Article] www.whxb.pku.edu.cn

*Corresponding author.Email:xlliucsu@126.com;Tel:+86-731-88652758.

The project was supported by the China Postdoctoral Science Foundation(20080431025),Natural Science Foundation of Hunan Province,China (08JJ3005),and Postdoctoral Science Foundation of Central South University,China(20071025).

中国博士后科学基金(20080431025),湖南省自然科学基金(08JJ3005)和中南大学博士后科学基金(20071025)资助

O641