基于表面间三棱锥体积测度的点云配准

张 梅 文静华 张祖勋 张剑清

1.贵州财经学院,贵阳,550004 2.武汉大学,武汉,430079

0 引言

三维激光扫描是近年来迅速发展起来的一种新型空间数据获取手段和工具,在物体建模研究与应用方面受到越来越广泛的关注。随着激光扫描技术的发展及成本的降低,这方面的研究受到越来越多的关注[1]。然而,由于激光扫描原理和物体本身形状的限制,使得重建出一个准确而高效的三维模型目前还存在着许多困难,其中之一便是点云的配准。

在三维扫描过程中,许多因素决定了无法通过单个视觉传感器一次扫描完成整个物体的测量。通常把物体表面分成多个局部相互重叠的子区域,从多个角度分别获取它们的表面信息,从而得到多个独立的三维点云,称为多视(multi—view)点云。在扫描不同的子区域时,所得三维点云在各自测量位置对应的局部坐标系下,而多次测量所对应的局部坐标系并不一致。把各次测量对应的局部坐标系统一到一个全局坐标系下即为多视点云的配准[2]。点云配准有手动配准、依赖仪器的配准和自动配准。通常我们所说的点云配准技术即是指最后一种[3]。点云自动配准技术是通过一定的算法或者统计学规律,利用计算机计算两片点云之间的错位,从而达到把两片点云自动配准的效果。

针对上述多视点云配准方法的不足,本文提出一种基于离散对应特征和表面间平均三棱锥体积误差测度的改进ICP算法来计算多视点云变换矩阵。先利用基于离散对应特征点的方法求出一个初始的位姿,再使用基于表面间平均三棱锥体积误差测度的改进ICP算法进行迭代求精。与传统ICP算法的比较结果表明,本文改进算法可以高效而精确地解算出点云模型配准所需的各种坐标变换参数。

1 初始位姿估计

利用离散的对应特征进行粗略配准以估计初始位姿。基于对应特征的配准方法,就是先设法在两个相邻视图的点云模型P和M(基准点云模型)中找到n(n≥3)组特征对(或称为对应特征),每一组特征对都对应了实际物体的同一特征。利用点云模型P中的n个特征(P1,P2,…,Pn)和点云模型M中的n个特征(M1,M2,…,Mn)的变换关系Mi=R0Pi+t0(i=1,2,…,n)来求解出刚性变换参数(R0,t0),从而实现粗略配准。

一般常被选作对应特征的几何特征是点[11],首先用基于几何特征的视觉技术目视判断得到初值:如拐角、折痕、边界,在两个相邻视图的点云模型中手工指定n(n＞3)组对应特征点,然后通过一个线性最小二乘最优化的过程求解出(R0,t0),最后将变换的(R0,t0)应用到点云模型P上得到其刚性变换后的点云模型P′=R0×P+t0,从而将两个点云模型P和M粗略配准到同一坐标系(M为基准点云模型)。

2 三棱锥体积计算

误差测度和有效点对的选择策略对ICP算法的配准精度和收敛速度有很大的影响[12-13],只有尽可能地排除偏离点的影响,定义一个能够真正反映深度像重叠区域吻合程度的误差测度,才能使算法具有更强的鲁棒性,得到更加准确的配准结果。现有的配准算法[14-15]在误差测度的选择上始终都没有跳出点对或者点面欧氏距离的范畴。本文提出另外一种衡量配准误差的概念:表面间平均三棱锥体积测度,将两片激光点云重叠区域间的三维空间三棱锥体积作为误差测度,并采用一种与之相匹配的点对选取策略完成三角网格的精确配准。

点云模型配准就是要找到输入点云P和目标点云 Μ之间的一个空间位置变换关系矩阵T(旋转矩阵R与平移向量t),使得某种形式的误差测度E在T下最小。目前,最常用的一种误差测度方法,是由Besl等[4]提出的对应点欧氏距离平方均值法:

式中,N为点云模型P上顶点的个数。

与式(1)中基于距离的误差测度不同,本文提出了一种基于点云数据重叠区域间平均体积的误差测度,如图1所示。

2.拓宽企业融资渠道。深化债券市场融资功能，引导企业通过发行企业债、公司债、中期票据、资产支持票据、短期融资券、超短期融资券、项目收益债等融资方式，扩大融资规模；发挥政府投资引导基金作用，支持产业链核心企业发起、引导社会资本共同参与设立产业创投基金，为产业链上下游企业提供资金支持。鼓励有条件的民营企业联合发起设立民营资本投资公司。设立广西并购引导基金，推动工业企业重组整合壮大。积极争取投贷联动试点，大力推动市场化法治化债转股工作。

本文改进算法的目的就是要找到一种适合进行空间位置关系变换的方法,使得两个点云模型重叠区域间的三维空间最小。两个点云模型重叠区域间点与对应三角形所夹的体积可以表示为

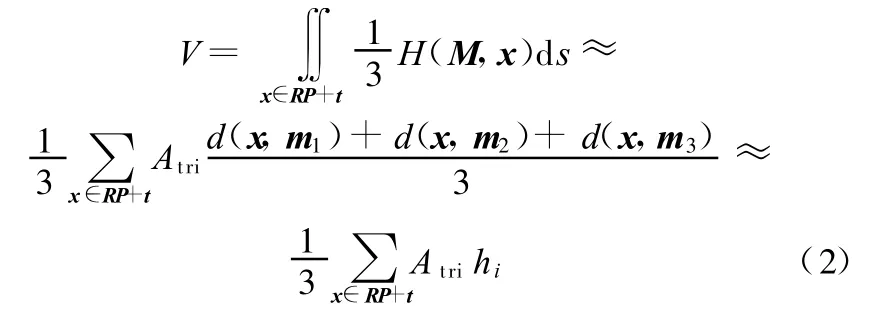
式中,x为点云RP+t上的顶点;H(M,x)为点x到点云模型M上所有顶点欧氏距离的最小值;d(x,mi)(i=1,2,3)为顶点x到3个顶点mi之间的距离;Atri为对应三角形的面积;hi为点云RP+t上顶点x到点云模型M上对应三角形的3个顶点距离的均值。

3 改进的迭代最近点(ICP)配准算法

3.1 基于平均三棱锥体积的误差测度

由式(2)可以定义误差测度为

实验结果表明,式(3)定义的误差测度具有较强的鲁棒性和较高的配准精度。

基于平均三棱锥体积的误差测度计算步骤如下:

(1)根据体积最小原则,找到点云P上所有点在点云M上的对应三角形。

(2)E(|T|)=0,N=0,对点云P上的每一个顶点x,①找到其对应三角形上的每一个顶点m1、m2、m3,并计算顶点 x到3个顶点之间的距离d(x,mi)(i=1,2,3)的值;②利用海伦公式:

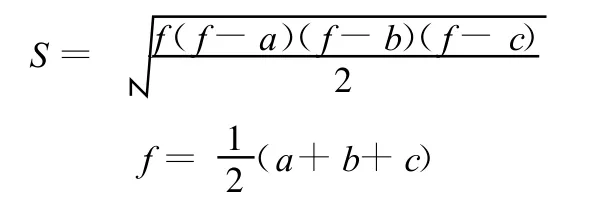
根据边长 a、b、c,求出m1、m2、m3所围三角形面积

3.2 基于平均体积误差测度的点云配准

假设两片点云数据向量P和M(将P配准到M),配准算法是首先利用基于离散对应特征点的方法得到刚体变换的初始估计。然后对P应用转换关系矩阵T(旋转矩阵R与平移向量t)生成P′;从P′中拾取一点p,到M中寻找与p最近的一点m,构成点对(p,m),去除间距特别大的对应点对,去除有顶点位于点云模型边界上的对应点对,最后形成有效点对集合(Ps,Ms);利用旋转向量,按照Gelfand等[13]的方法线性化旋转矩阵R,从而通过求解一个线性系统得到新的变换关系矩阵Tk。计算Ps与Ms所夹的三维空间平均体积测度误差,如果小于设定的值则结束,否则进行下次迭代。改进的最近点迭代配准算法步骤如下:

(1)利用基于离散对应特征点的方法计算初始位姿(R0,t0)。

(2)k=0,迭代开始:①k←k+1,对点云模型P中的所有点应用转换矩阵Tk—1(旋转矩阵Rk—1 与平移向量tk—1)生成P=Rk—1P+tk—1;②计算Tk—1下点云模型M和P所夹三维空间的平均体积误差测度E(Tk—1);③找到点云模型P中所有点在M上的最近对应点,并取所有对应点对中距离最近的90%作为有效的对应点对;④利用旋转向量,按照Gelfand等[13]的方法线性化旋转矩阵Rk,从而通过求解一个线性系统得到新的变换关系矩阵Tk,直到 E(|Tk—5|)—E(|Tk|)≤10—4或者k=kend,迭代终止。

(3)输出最优的变换关系Tk=(Rk,tk)。

4 实验结果与分析

将挂钩放在旋转平台的中心,旋转平台每转动10°,三维激光扫描仪 VIVID910扫描一次,分别获取在旋转角度为 0°、10°、20°、30°、…、350°时的挂钩激光点云数据。实验目的在于对依次相邻视点获取的激光扫描数据进行配准,验证本文提出的改进迭代最近点算法的有效性、正确性和可行性,比较本文方法与以往方法的配准精度与收敛速度,为后续曲面物体深度图像的分割提供完整三维几何模型。

首先对挂钩的 36片激光点云用文献[11,16-17]中的方法进行平滑、滤波、去噪、简化等数据预处理。然后选取角度为0°的位置作为空间参考坐标系,依次对其他视角获取的点云数据配准到该参考坐标系。将多视角点云模型的配准转化成依次进行的两两配准,并按照本文的改进算法完成。

限于篇幅,只用初始位置0°(基准模型)和旋转10°两视角的点云模型进行配准,并将其配准结果、配准精度和时间效率与文献[18]基于对应点距离平方均值误差测度的算法进行比较。图2a所示为位于初始位置0°、用三维激光扫描仪VIVID910得到的基准点云模型,含有51 322个三维数据点;图2b所示为旋转10°后用三维激光扫描仪VIVID910得到的点云模型,含有51 397个三维数据点。

图3a所示为文献[18]算法的配准结果,该算法利用两个三维点云模型之间的平均欧氏距离作为误差测度。其中,图3b所示为本文算法的配准结果。对照图2可以看出,图3b的配准结果要明显优于图3a的配准结果。基于对应点对距离的配准算法往往陷入局部最优而无法得到正确的空间变换关系,而本文算法却可以得到比较精确的配准结果。

图4所示为图3中两种配准算法收敛速度的比较。由于配准误差的单位不一样(本文算法的单位是mm3,文献[18]算法的单位是mm),因此分别在两幅图中显示了两种算法迭代100次的误差分布。表1所示为图3中配准结果的定量比较,这些结果是在Pentium Ⅳ,2.66GHz CPU,960MB内存的PC机上计算得到的,开发平台是MATLAB7.0。

由于利用海伦公式求解三角形面积需要更多的计算,因此本文算法每一次迭代的运行时间会略长。然而,如表1中有效点对数量的统计,由于满足条件的三角形对的数量要远远小于对应点对的数量,因此,本文算法只需较少的时间就可以计算出新的空间位置变换关系,从而保证了每一次迭代的运行时间和文献[18]算法相比差距不大,再考虑迭代次数,显然本文算法具有更快的收敛速度。

表1 图3中配准结果的定量比较

图5所示是按照本文改进算法和实验方法依次完成所有36个挂钩点云模型两两配准后,得到的完整挂钩多视角点云模型配准融合三维几何曲面模型。

5 结束语

本文在分析了现有点云模型配准方法的基础上,提出了一种基于表面间点与对应三角形所夹三棱锥平均体积误差测度的三角网格精确配准算法,与现有ICP框架下的迭代配准方法相比,该算法主要有两个贡献:一是提出了表面间平均体积测度的概念,该测度衡量的不是对应点对或者点面之间的欧氏距离,而是点与对应三角形所夹三棱锥的平均体积;二是采用一种与表面间平均体积测度相匹配的选点策略,通过从点与对应三角形的质心所形成的点对中选取最近对应点对,有效地排除了偏离点的影响,确保了算法的精度和速度。

[1]戴静兰,陈志杨,叶修梓.ICP算法在点云配准中的应用[J].中国图像图形学报,2007,12(3):517-521.

[2]路银北,张蕾,普杰信,等.基于曲率的点云数据配准算法[J].计算机应用,2007,27(11):2766-2769.

[3]朱延娟,周来水,张丽艳.散乱点云数据配准算法[J].计算机辅助设计与图形学学报,2006,18(4):475-480.

[4]Besl P J,McKay N D.A Method for Registration of 3—D Shapes[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(2):239-256.

[5]Chen Y,Medioni G.Object Modeling by Registration of Multiple Range Images[C]//Proceedings of IEEE International Conference on Robotics and Automation.Sacramento,CA,1991:2724-2729.

[6]Blais G,Levine M D.Registering Multi—view Range Data to Create 3D Computer Graphics[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1995,17(8):820-824.

[7]Li Q,Griffiths J G.Iterative Closest Geometric Objects Registration[J].Computers and Mathematics with Applications,2000,40(10):1171-1188.

[8]张学昌,习俊通,严隽琪.基于点云数据的复杂型面数字化检测技术研究[J].计算机集成制造系统—CIMS,2005,11(5):727-731.

[9]Helmut P,Stdfan L,Michael H.Registration without ICP[J].Computer Vision and Image Understanding,2004,95:54-71.

[10]Masuda T,Sakaue K,Yokoya N.Registration and Integration of M ultiple Range Images for 3—D Model Construction[C]//Proceedings of the 13th International Conference on Pattenrn Recognition.Vienna,1996:879-883.

[11]吴敏,周来水,王占东,等.测量点云数据的多视拼合技术研究[J].南京航空航天大学学报,2003,35(4):552-555.

[12]贾云得.机器视觉[M].北京:科学出版社,2000.

[13]Gelfand N,Ikemoto L,Rusinkiewicz S,et al.Geometrically Stable Sampling for the ICP Algorithm[C]//Proceedings of the 4th International Conference on 3D Digital Imaging and Modeling.Banff,2003:260-267.

[14]张鸿宾,谢丰.基于表面间距离度量的多视点距离图像的对准算法[J].中国科学 E辑:信息科学,2005,35(2):150-160.

[15]Turk G,Levoy M.Zipped Polygon Meshes from Range Image[C]//Proceedings of ACM,Siggraph.Orlando,1994:311-318.

[16]李剑.基于激光测量的自由曲面数字制造基础技术研究[D].杭州:浙江大学,2001.

[17]Dalley G,Flynn P.Range Image Registration:a Software Platform and Empirical Evaluation[C]//Proceedings of the 3rd International Conference on 3D Digital Imaging and Modeling.Quebec,2001:246-253.

[18]Pulli K.Multi—view Registration for Large Data Sets[C]//Proceedings the 2nd International Conference on 3D Digital Imaging and Modeling.Ottawa,1999:160—168.