球面配流副二维稳态压力场的数值求解方法研究

李小金 苑士华 胡纪滨

北京理工大学车辆传动国家重点实验室,北京,100081

0 引言

缸体与配流盘之间的平衡分析是轴向柱塞液压元件设计中不可缺少的环节,而精确求得配流副间油膜的压力场则是平衡分析的关键。国内外学者针对平面配流副进行了大量的研究工作。Shute等[1]通过电模拟法计算了平面配流副上高低压油槽间过渡区域的压力分布,并给出了等效延伸角。Yamaguchi等[2-3]、Pan等[4]、陈卓如等[5]、王有荣等[6]利用不同形式的数值计算方法给出了平面配流副压力场分布的数值解。而针对目前应用较多的球面配流副的研究则极少,且多数为以测量油膜形状为目的的试验研究[7-8]。在压力场研究方面,基本上采用忽略过渡区压力场的方法,只研究一维径向压力场分布[9],这与实际的情况通常有较大的偏差。

油膜的二维压力场可由雷诺方程求得。雷诺方程是非线性二阶偏微分方程,通常很难求得解析解,需要使用计算流体力学方法进行数值求解。有限差分法是其中发展最为成熟、应用最为广泛的数值求解方法之一。有限差分法采用结构化网格进行计算,由于配流副油膜形状复杂,因此,为保证网格质量及求解精度,需要在求解的物理区域建立贴体网格,贴体网格在计算域中将被映射为矩形网格。贴体网格的生成方法主要有三种:代数方法、微分方程方法和保角变换方法[10],其中微分方程方法可以处理各种不规则边界,应用最为广泛。但微分方程法需要以平面直角坐标系作为物理区域的坐标系,而对于球面配流副,其物理区域为球面,因此,无法将物理区域通过平面直角坐标系表示。本文探讨球面坐标系下贴体网格的生成方法,解决球面配流副二维压力场的求解问题。

1 贴体坐标系下球面配流副的雷诺方程

本文在文献[11]中提到的雷诺假设条件下,利用不可压缩黏性流体的雷诺方程求解球面配流副压力场。张量形式的雷诺方程表达式为:

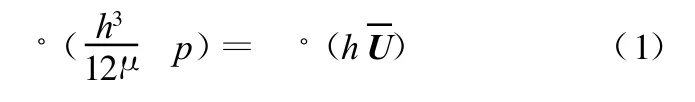
由雷诺假设,在油膜厚度方向不计压力的变化,因此球面配流副的压力场可以简化为二维稳态压力场。式(1)是可以直接在球坐标系下进行数值求解的,但由于配流副的形状复杂,求解时会给边界条件的描述带来很大困难,同时数值求解的精度也不高。因此通常选择在与油膜边界贴合的贴体坐标系下对雷诺方程进行求解[12-13]。设贴体坐标系为(ξ,η),球面油膜所在球面坐标系为(θ,φ)。应用张量分析的相关知识[14],并将贴体坐标系下的速度分量以球坐标系下的缸体的转速 ω表示。最终,式(1)在贴体坐标系下可展开为

2 贴体网格的生成方程

球面配流副属于空间曲面,因此已有的网格生成方程并不适用。本文将推导适用于球面配流副的贴体网格生成方程。由微分几何学可知,空间曲面上的坐标系均应满足方程[15]:

式中,r为曲面上任意一点的矢径;rα、rβ为坐标曲线在该点的切矢量;ξα、ξβ为坐标系的坐标;L为微分算子;g为度规张量分量gαβ的行列式的值;Δ2为Beltrami二阶微分算子;n为空间曲面的单位法矢量为空间曲面的平均曲率。

式中,P、Q为控制函数。

式(4)、式(5)即为油膜贴体网格的生成方程。通过生成方程求解贴体坐标系中每个网格点在球坐标系中的坐标值即可自动生成油膜贴体网格。当不对贴体网格进行特定控制时,可令P=Q=0,而使用不同形式的控制函数可以对贴体网格的局部密度产生不同的控制效果。常用的控制函数为[13]

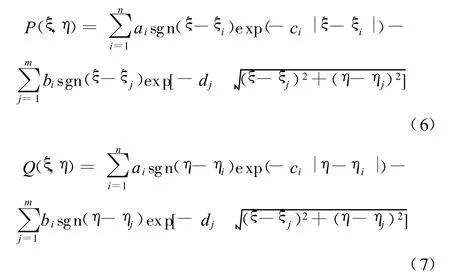
球面配流副上存在多个油口(对于液压泵/液压马达为2个,对于液压变压器为3个),而且各个油口的包角、压力边界条件也不尽相同。为了简化雷诺方程的求解,形成一套统一的建模方法,本文采用在各个油口分别建立贴体坐标系生成贴体网格,然后采用将其两两耦合的方法建立整个球面配流副上的贴体网格。这种建模方法的优点在于贴体网格的生成与油口数量及包角无关,而且对于各个贴体坐标系,雷诺方程都有相同的形式,仅仅边界条件的数值不同而已。如图1所示,斜轴式液压变压器的球面配流副共有A、T、B 3个油口,因此作切口7—8、9—10、11—12,将物理域分为3块,分别建立3个贴体坐标系。可以看出,在物理域中边界复杂的空间曲面在计算域中被映射为3个矩形平面。A、T、B口复杂的压力边界在计算域中分别被映射为横坐标ξ的等值线1—1′、3 —3′和5—5′;回油压力边界在计算域中分别被映射为横坐标ξ的等值线2—2′、4—4′和6—6′,其中 ,切口边界 7—8 、9 —10、11—12为油口间的耦合边界,并不是压力边界,该处的压力值需在计算过程中确定。综上所述,物理域中原本复杂的油膜边界条件在计算域中变得十分简单,而求解区域在计算域中也转化为标准的矩形区域,从而大大降低了雷诺方程的求解难度,提高了求解精度。

3 网格生成方程与雷诺方程的求解

网格生成方程(式(4)、式(5))与雷诺方程(式(2))均为二阶偏微分方程,可以用常规的有限差分迭代法在图1b所示的计算域中求解。图2所示为完整的求解流程。

这里需要说明的是,在迭代求解网格生成方程(式4)时,会发现在该方程的若干系数中还包含待求变量θ的三角函数项,这样迭代方程将是隐式方程,直接求解将极大影响计算速度。为此,本文提出:在迭代过程中使用待求变量θi,j周围的4个点的均值替换三角函数项中出现的θi,j,进而将迭代方程转化为显式方程的形式,从而大大提高计算速度。表1所示为网格密度不同、但精度相同条件下使用显式方程与隐式方程求解所花费的时间。从表1可以看出,采用近似平均的方法将隐式方程转化为显式方程求解明显缩短了求解时间。

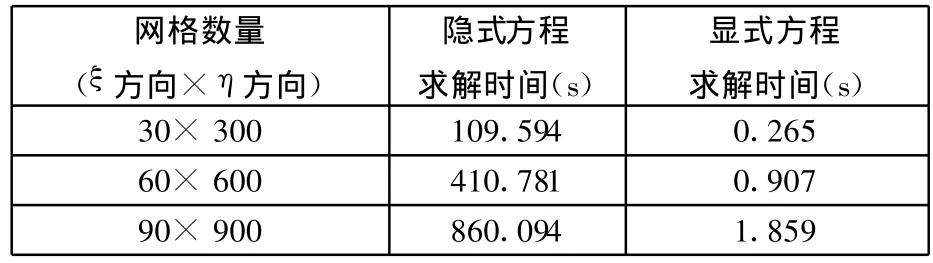
表1 隐式方程与显式方程求解时间对比

求解雷诺方程前,还需确定配流副上各点的油膜厚度。球面配流副的间隙可认为是由两个球面半径相同的球面沿轴向偏移形成的偏心圆球缝隙。球面配流副上各点油膜厚度可表示[9]为

4 算例及讨论

本文在MAT LAB环境下以斜轴式液压变压器为例,对球面配流副的二维稳态压力场进行了编程求解,并针对不同油膜状态下的压力分布特性进行比较分析。计算时液压变压器球面配流副的相关参数为:球面半径R=112mm,密封带半径 r1=6.75mm、r2 = 10.35mm、r3=20.75mm、r4=24mm,油口包角 120°均布,配流盘控制角度60°,A口压力20MPa,T口压力0.5MPa,B口压力20MPa,回油压力0.1MPa。

图3所示为求解网格生成方程生成的球面配流副贴体网格。为显示清晰,图中所示的网格数量为30×300(3个计算域,每个计算域划分为10×100个网格)。

图4a所示为e=5μ m 、ω=0时的油膜压力场分布。可以看出压力场关于x轴呈对称分布。当两相邻油口压力水平较为接近时,油口间过渡区域大部分的压力水平接近油口压力。显然,在这种情况下过渡区域的压力场是不能假设为零的。图4b为e=10μ m、ω=2000 r/min时的油膜压力场分布。可以看出,压力场分布与图4a完全相同。

综上,缸体与配流盘处于偏心状态(对配流副进行理论分析时常假设为这一状态)时压力场分布与偏心距、缸体转速无关。这一点与常规的理论计算结果是一致的,这也是应用剩余压紧力理论对配流副进行设计以及计算时无法直接确定油膜厚度的原因。此外,本文完全按照真实油膜区域求解,因而可以获得包括过渡区域在内的二维稳态压力场分布。值得注意的是,过渡区域的压力场在相邻油口压力接近时不能假设为零,其产生的分离力是不能被忽略的,否则将给分离力的计算造成较大的误差。

李小宁[9]给出了忽略过渡区压力场(认为只在径向上存在压力梯度)的情况下,同轴偏心时球面配流副密封带径向压力场分布的解析解。这一解析解虽然不能描述过渡区的压力分布,但是在描述油口区域密封带的压力分布时是准确的。图5所示为配流盘A口区域内外密封带压力分布的数值解与解析解的对比图。可以看出,在贴体坐标系下求出的数值解与解析解非常接近。

由于配流副尺寸通常较小,压力场也很难通过试验测得。有关球面配流副过渡区域的压力场分布的试验数据几乎没有,因此无法直接对计算结果进行验证。而平面配流副是进行理论与试验研究时最常使用的配流副,对其过渡区域压力场的研究则相对较多一些。当球面半径很大时,可以认为球面配流副即近似为平面配流副。因此,作为对比和验证,本文使用球面配流副的贴体网格生成方程及相应的雷诺方程进行平面配流副的近似计算,计算时取球面半径R=100m、配流盘半径r4=30mm。由简单的几何计算可知,此时配流盘的球面高度仅为4.5μ m,完全满足通常平面配流盘平面度不大于5μ m的要求,这样的近似是可行的。图6所示为取量纲一宽度=0.4、量纲一槽宽=0.4、高低压槽端部区夹角ε=32°时,计算所得量纲一等压力分布线与文献[1]中电模拟法结果的对比。可以看出,两者非常接近。图7所示为取=0.4时,计算得出的等效延伸角与文献[1]中结果的对比。可以看出,两者误差很小,绝大部分结果误差小于0.5°。在实际应用中等效延伸角变化1°大约相当于分离力变化1%,这样的误差完全可以接受。

5 结论

(1)推导出了基于球面坐标系的贴体网格生成方程,在贴体坐标系下求解雷诺方程得到了球面配流副的二维稳态压力场,为今后进一步开展球面配流副二维压力场特性的理论研究提供了条件。

(2)针对迭代求解贴体网格生成方程时迭代方程为隐式方程的问题,提出了通过近似平均将隐式方程转化为显式方程的方法,可在不降低求解精度的条件下大大缩短求解时间。

(3)对液压变压器球面配流副不同工况下的压力场分布进行了计算求解。计算结果表明压力场分布与油膜厚度、缸体转速无关。油口区域密封带径向压力分布的计算结果与解析解相吻合。此外,当两相邻油口压力接近时,过渡区域的压力场不能忽略。

(4)用球面配流副近似平面配流副进行了压力场计算。结果表明本文得出的计算结果与采用电模拟法得到的压力场分布、等效延伸角等结果非常接近,证明本文提出的二维压力场计算方法正确、可行。

[1]Shute N A,Turnbull D E.The Thrust Balancing of Axial Piston Machines[R].Bedford:BHRA,1963.

[2]Yamaguchi A.Pressure Distribution on Valve Plate of Axial Plunger Pumps and Motors[J].Sensankenkyu,1966,18(7):18-20.

[3]Yamaguchi A,Fujitani Y,Isoda Y.Characteristics of Fluid Film between a Valve Plate and a Cylinder Block of Axial Piston Pumps and Motors[J].Japan Hydraulics and Pneumatics Society,1984,15(4):314-322.

[4]Pan H C,Sheng J C,Lu Y X.Finite Difference Computation of Valve Plate Fluid Film in Axial Piston Machines[J].Int.J.Mech.Sci.,1989,31(10):779-791.

[5]陈卓如,范莉,金朝铭.液压马达新型端面配流副液压分离力的数值求解及分析[J].机床与液压,2000(2):7-9.

[6]王有荣,刘恒龙,柯坚,等.水压轴向柱塞泵配流副流场的CFD解析[J].液压与气动,2007(7):21-24.

[7]Kim J K,Kim H E,Lee Y B.Measurement of Fluid Film Thickness on the Valve Plate in Oil Hydraulic Axial Piston Pumps(PartII:Spherical Design Effects)[J].Journal of M echanical Science and Technology,2005,19(2):655-663.

[8]王彬,周华,杨华勇,等.基于电液反馈的轴向柱塞机械润滑试验系统[J].哈尔滨工程大学学报,2008,29(4):348-353.

[9]李小宁.斜轴式轴向柱塞泵主体部件的计算机辅助设计系统[D].哈尔滨:哈尔滨工业大学,1989.

[10]周正贵.计算流体力学基础理论与实际应用[M].南京:东南大学出版社,2008.

[11]温诗铸,黄平.摩擦学原理[M].2版.北京:清华大学出版社,2002.

[12]Thompson J F,Thames F C,Mastin C W.Automatic Numerical Generation of Body—fitted Curvilinear Coordinates System for Field Containing Any Number of Arbitrary Two—Dimensional Bodies[J].Journal of Computation Physics.1974,15:299-319.

[13]Thompson J F.Numerical Grid Generation:Foundation and Application[M].North Holland:Elsevier Science Publishing Co.,Inc.,1985.

[14]吕盘明.张量算法简明教程[M].合肥:中国科学技术大学出版社,2005.

[15]Warsi Z U A.A Note on the Mathematical Formulation of the Problem of Numerical Coordinate Generation[J].Quarterly of Applied M athematics.1983,41:221-236.