构造向量证明竞赛中的分式不等式
2010-12-01 02:10
中学教研(数学) 2010年1期
●
(枞阳横埠中学 安徽安庆 246725)
构造向量证明竞赛中的分式不等式
●章礼抗
(枞阳横埠中学 安徽安庆 246725)
在数学竞赛中,不等式问题一般都难以下手.这里笔者运用m·n≤|m||n|证明数学竞赛中的一类分式不等式,望读者能从中得到启发.
1 m·n≤|m||n|直接应用
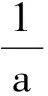
(1990年日本IMO选拔赛题)
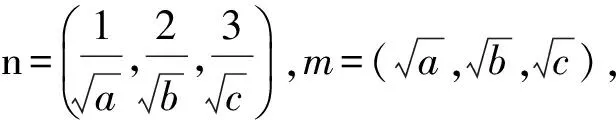
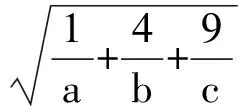
从而
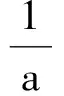
推广(1)把条件a+b+c=1变为a+b+c≤1,命题仍然成立.
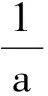
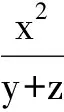
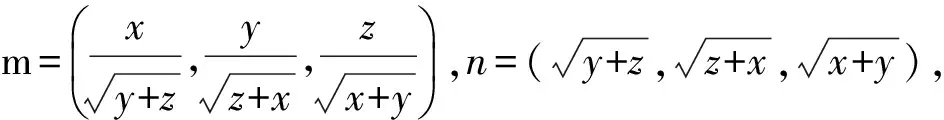
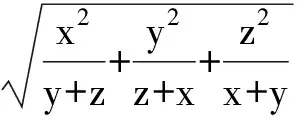
从而
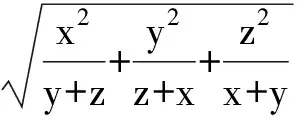
因此
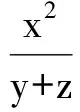
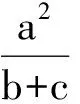
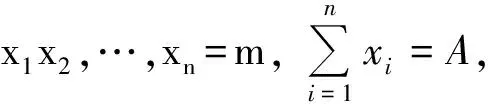
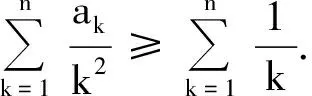
(第20届IMO试题)
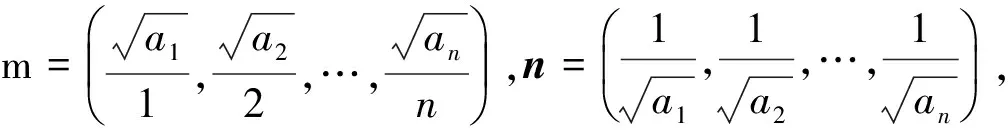
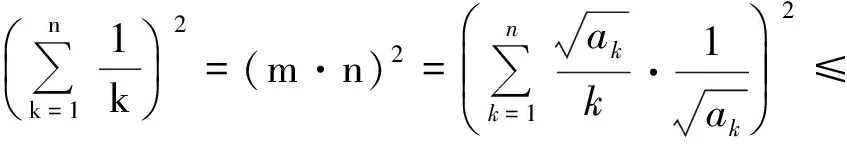
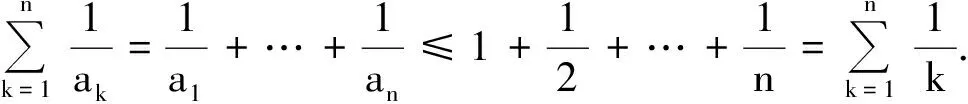
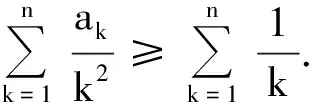
例4设a,b,c,d是满足ab+bc+cd+da=1的实数,求证:
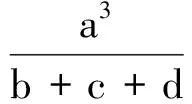
(第31届IMO预选题)
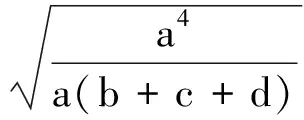
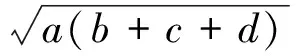
则
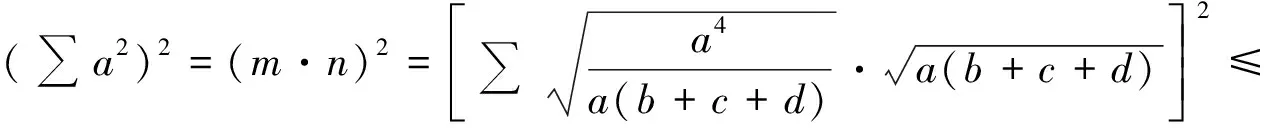
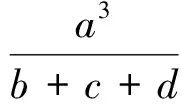
因此
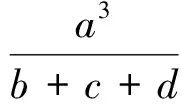
其中
∑a(b+c+d)=2(ab+bc+cd+da+ac+bd)≤3(a2+b2+c2+d2).
故命题得证.
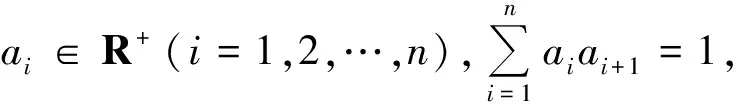
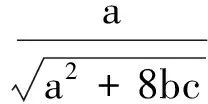
(第42届IMO试题)
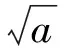
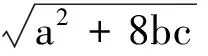
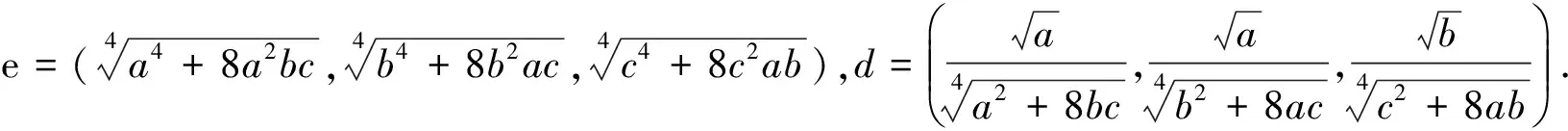
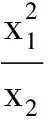
(1984年高中数学联赛试题)
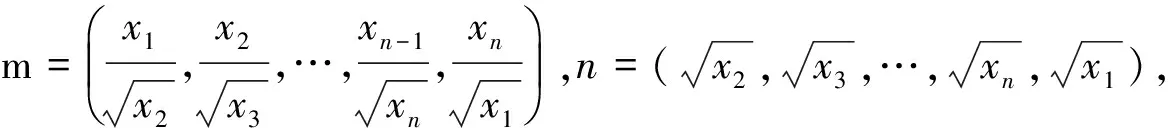
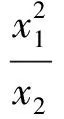
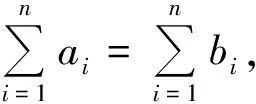
(1991年亚太地区数学竞赛试题)
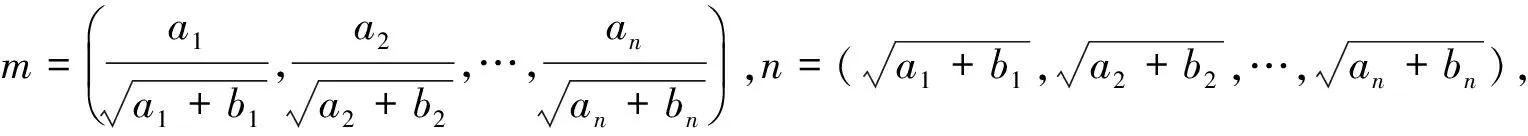
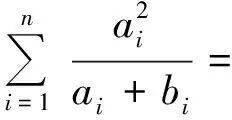
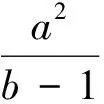
(第26届独联体数学奥林匹克竞赛试题)
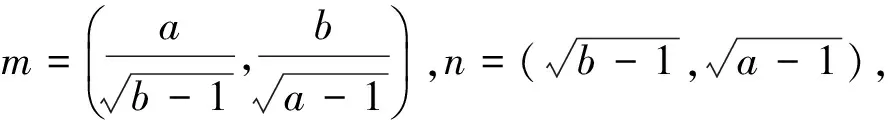
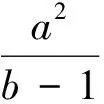
3 2种形式都可证明
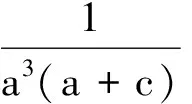
(第36届IMO试题)
证法1因为abc=1,所以
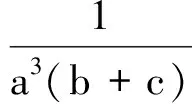
于是原不等式可变形为
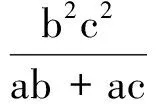
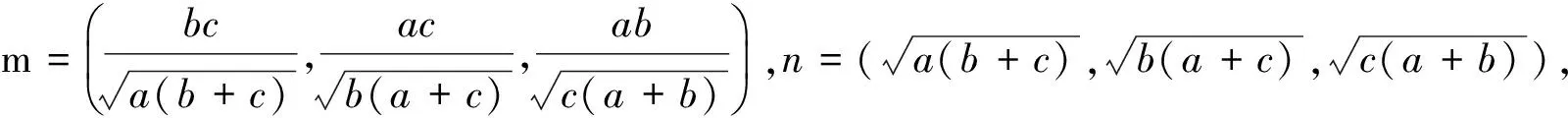
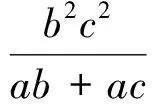
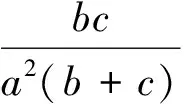
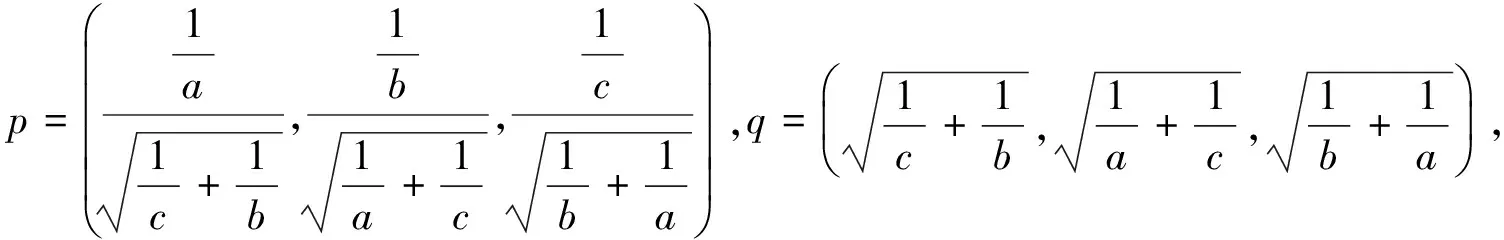
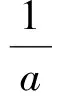
即
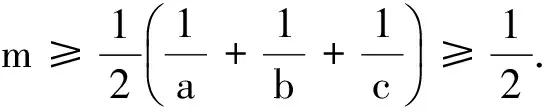
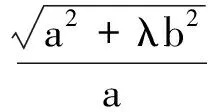
(《数学通报》2006(6)问题1 613)
解原不等式等价于
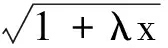
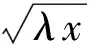
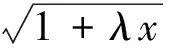
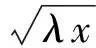
由|a|+|b|+|c|≥|a+b+c|,得
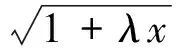
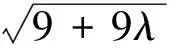
由此证明该命题可推广为:
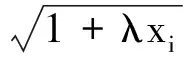
这类构造向量证明分式不等式类型的方法,关键是要对先要证的不等式进行仔细地分析,然后才构造向量.
猜你喜欢
意林彩版(2022年1期)2022-05-03
安庆师范大学学报(自然科学版)(2020年3期)2020-09-07
中学生数理化·七年级数学人教版(2018年12期)2019-01-31
中学生数理化·中考版(2017年3期)2017-11-09
中学生数理化·七年级数学人教版(2017年12期)2017-04-18
中学生数理化·七年级数学人教版(2017年12期)2017-04-18
表面工程与再制造(2014年2期)2014-02-27
对联(2011年24期)2011-11-20
对联(2011年18期)2011-11-19
对联(2011年6期)2011-11-19

