关于等周长方体的几个问题
2010-12-01 02:09
中学教研(数学) 2010年1期
● ●
(沂水职教中心 山东沂水 276400) (许家湖镇第一初级中学 山东沂水 276400)
关于等周长方体的几个问题
●耿立顺●耿立合
(沂水职教中心 山东沂水 276400) (许家湖镇第一初级中学 山东沂水 276400)
对于2个长方体,若它们的三度(长、宽、高)均为整数且和相等,则称这样的2个长方体为等周长方体.关于等周长方体,本文给出并解答如下几个问题:
问题1是否存在2个不同的长方体,等周且对角线相等.
问题2是否存在2个不同的长方体,等周且全面积相等.
问题3是否存在2个不同的长方体,等周且体积相等.
解决这些问题,利用“逆转数组”较为容易.为了引出逆转数组的概念,笔者需提及文献[1]中曾给出的等式组:
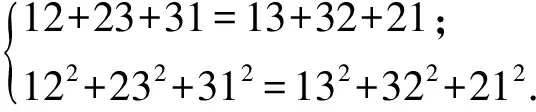
一般地,若
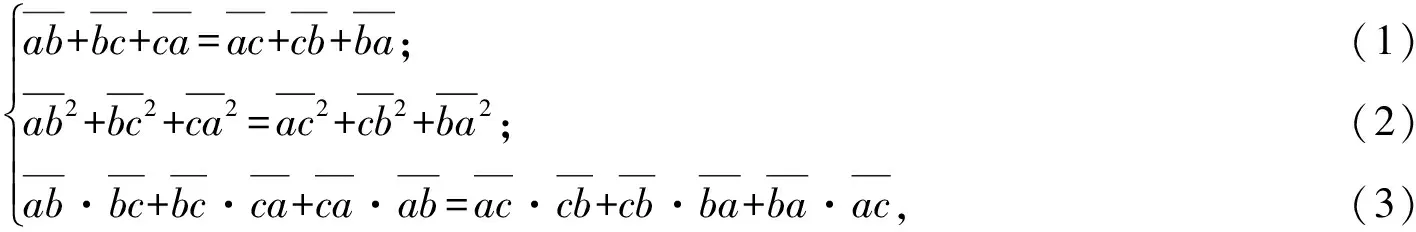
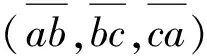
结论1若2个长方体的三度互为逆转数组,则这2个长方体等周且对角线相等.
结论2若2个长方体的三度互为逆转数组,则这2个长方体等周且全面积相等.
若2个长方体的三度互为逆转数组,则它们的体积相等吗?
回答是否定的.用反证法可以证明之.

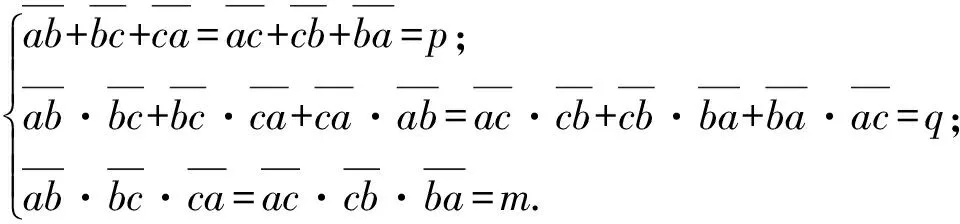
由逆转数组作三度构成的2个长方体体积不相等,但仍可借助逆转数组解决问题3.
即
(10a+b)(10b+c)(10c+a+x)=(10b+a)(10c+b)(10a+c+x).
展开并整理得
11(a-c)bx=10(a-b)(b-c)(c-a),
解得
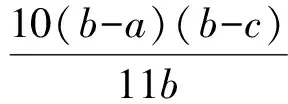



由此得到,长方体(110,202,38)与长方体(209,40,101)等周且体积相等.
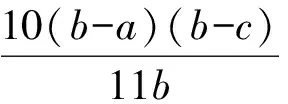
[1] 耿立顺.关于自然数与等幂和的一些性质[J].中学数学,1996(11):14-17.
猜你喜欢
电脑报(2022年13期)2022-04-12
电脑报(2020年24期)2020-07-15
东坡赤壁诗词(2019年5期)2019-11-14
中国民政(2019年13期)2019-08-06
中国公路(2017年18期)2018-01-23
电脑爱好者(2017年22期)2017-12-04
中学生数理化·八年级数学人教版(2016年2期)2016-04-13
中学生数理化·八年级数学人教版(2016年3期)2016-04-13
小雪花·成长指南(2015年7期)2015-08-11
大众考古(2015年9期)2015-06-26

