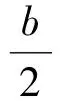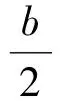几何概型不“孤单”
●
(华罗庚中学 江苏金坛 213200)
几何概型不“孤单”
●钱辉
(华罗庚中学 江苏金坛 213200)
若事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概型,它的特点是无限性和等可能性.在教学中,经常会遇到与其他多个知识点融合而形成的背景新颖、能力要求较高、构思独特的几何概型问题.
1 与随机数相关的几何概型
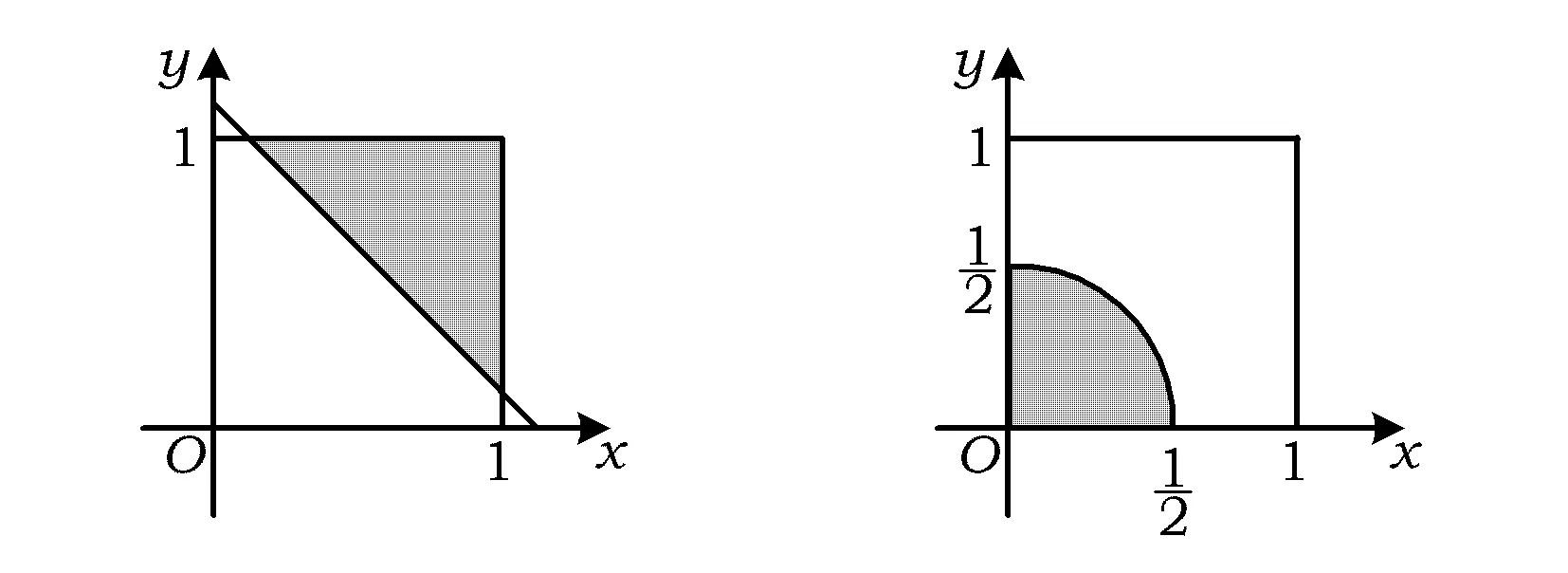
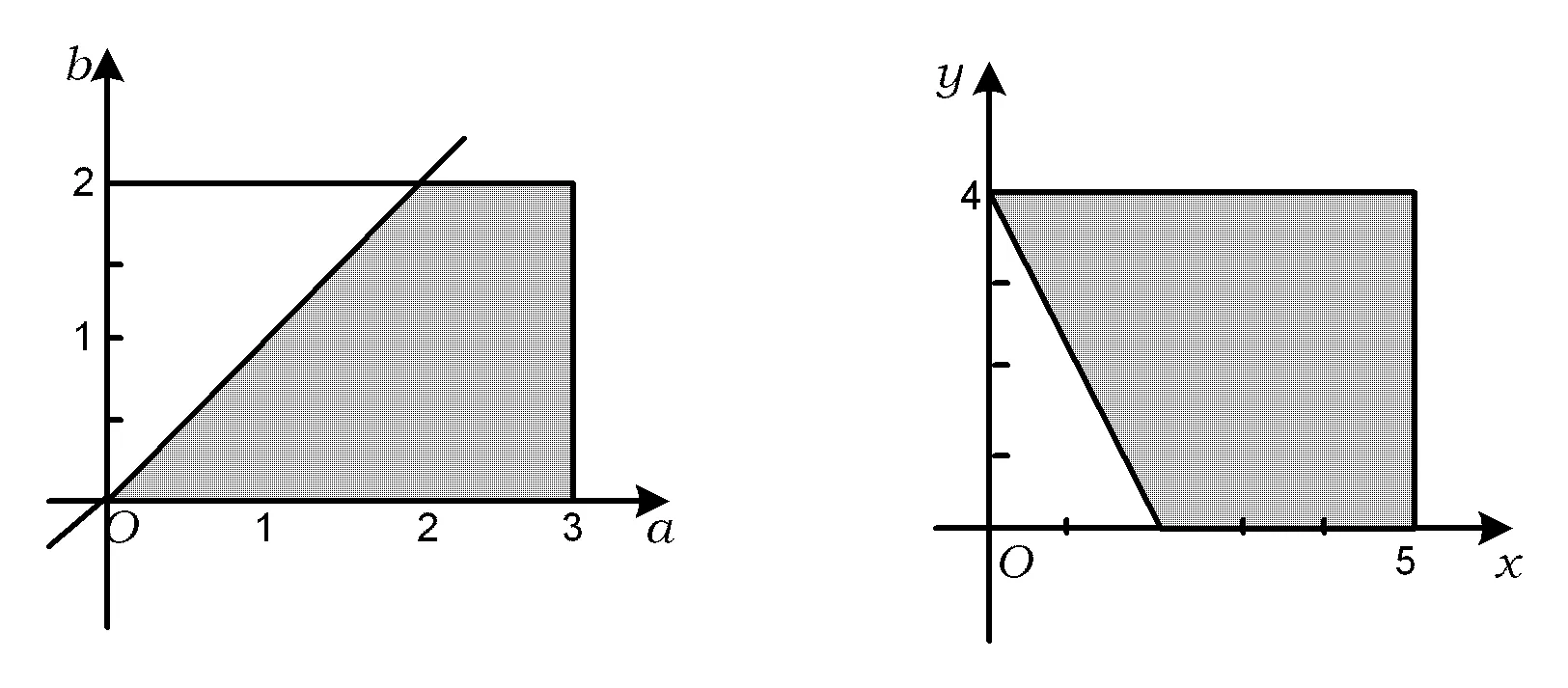
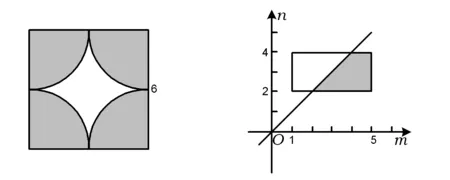
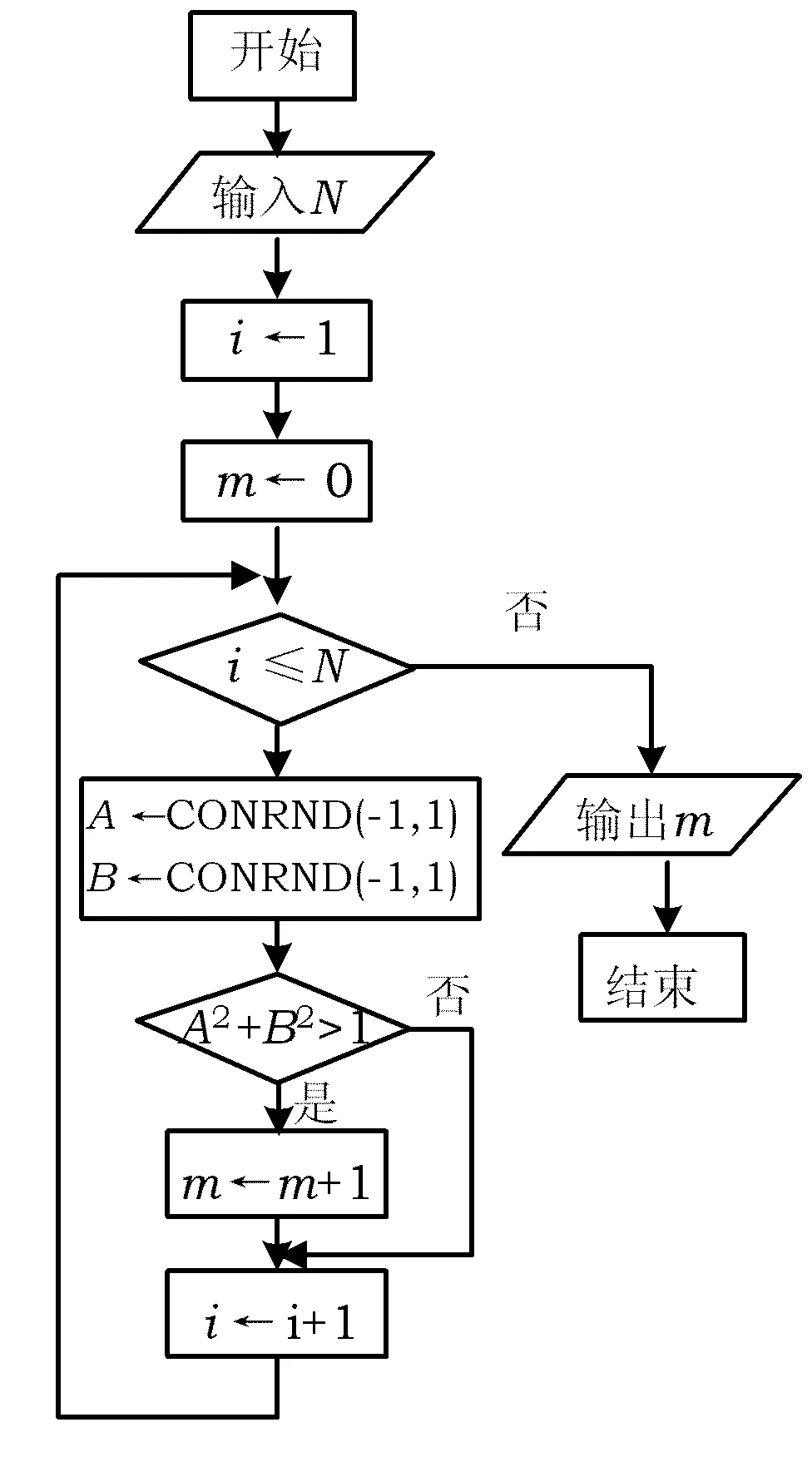
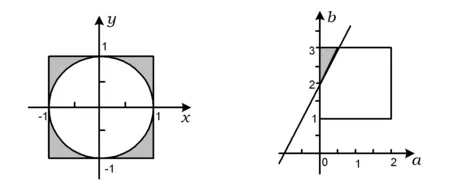
例1用计算机随机产生有序二元数组(x,y)满足0 (1)两数之和大于1.2; (2)两数平方和小于0.25. 解(1)记“两数之和大于1.2”为事件A,则x+y>1.2,因此事件A发生即表示点(x,y)落入图1中的阴影部分.而点落在正方形内任一点的机会都是均等的,于是事件A的概率应等于阴影部分的面积与正方形面积之比,所以 图1 图2 例2函数f(x)=x2-x-2,x∈[-5,5],对任意x0∈[-5,5],使f(x0)≤0的概率为多少? 图3 解记“任意x0∈[-5,5],使f(x0)≤0”为事件A,易知f(x)的2个零点为xC=-1,xD=2.在[-5,5]中任取一实数x即相当于在线段AB上任取1个点,事件A发生即恰好取到线段CD上一点,事件A包含的基本事件为图3中线段CD的长度,所有基本事件为线段AB的长度,因此 例3设关于x的一元二次方程x2+2ax+b2=0,若a是区间[0,3]中任取的1个数,b是区间[0,2]中任取的1个数,求上述方程有实根的概率. 解(1)记“方程有实根”为事件A,在直角坐标平面上,坐标(a,b)表示的点均匀落在如图4所示的矩形区域内,事件A发生即对应的点落在满足Δ=(2a)2-4b2≥0的区域内,因此 图4 图5 例4在集合{(x,y)|0≤x≤5,0≤y≤4}内任取1个元素,能使不等式2x+y-4≥0成立的概率是多少? 解记“不等式2x-y-4≥0成立”为事件A,如图5所示,集合{(x,y)|0≤x≤5,0≤y≤4}为矩形内(包括边界)所有点的集合,集合{(x,y)|2x+y-4≥0}表示坐标平面内直线2x+y-4=0右上方(包括直线)的点的集合,因此 例5一只蚂蚁在边长为6的正方形区域内随机地爬行,则其恰在离4个顶点距离都大于3的地方的概率为多少? 解记“蚂蚁恰在离4个顶点距离都大于3的地方”为事件A,如图6所示,蚂蚁落在正方形区域内任一点是等可能的,而事件A发生即蚂蚁落在了图6中所示的空白部分,因此 图6 图7 例6在1 L高产小麦种子中混入了一种带麦锈病的种子,从中随机取出10 mL,则取出的种子中含有麦诱病的种子的概率是多少? 解病种子在这1 L中的分布可以看作是随机的,取得的10 mL种子可视作构成事件的区域,1 L种子可视作试验的所有结果构成的区域,可用“体积比”公式计算其概率. 记“含有病种子”为事件A,则 因此取出的种子中含有麦诱病的种子的概率是0.01. 图8 例8定义函数CONRND(a,b)是产生区间(a,b)上的任何一个实数的随机数函数,如图8所示的程序框图可用来估计π的值.现在N输入的值为100,结果m的输出值为21,则由此可估计π的近似值为多少? 解在算法的流程图中,A,B分别是产生在(-1,1)中的随机数,故在直角坐标系中,由A,B组成的有序数组(A,B)为坐标的点落在“-1 即 解得 π≈3.16. 图9 图10 例9已知集合A={x|-1≤x≤0},集合B={x|ax+b·2x-1<0,0≤a≤2,1≤b≤3}.若a,b∈R,求A∩B=φ的概率. 解因为a∈[0,2],b∈[1,3],所以(a,b)对应的区域为边长为2的正方形.令 f(x)=ax+b·2x-1,x∈[-1,0], 则 f′(x)=a+bln2·2x. 因为 a∈[0,2],b∈[1,3], 所以 f′(x)>0. 即 2a-b+2≤0. 所以满足A∩B=φ的(a,b)对应的区域为如图9中所示的阴影部分,于是 几何概型虽然描述的是概率问题,可是它很容易与其他知识点相结合,以上通过几个例子概括地叙述了这类问题的主要题型,其他的一些问题这里就不再累述了.
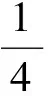
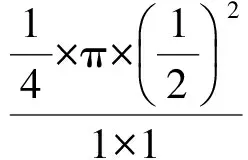
2 与函数相关的几何概型
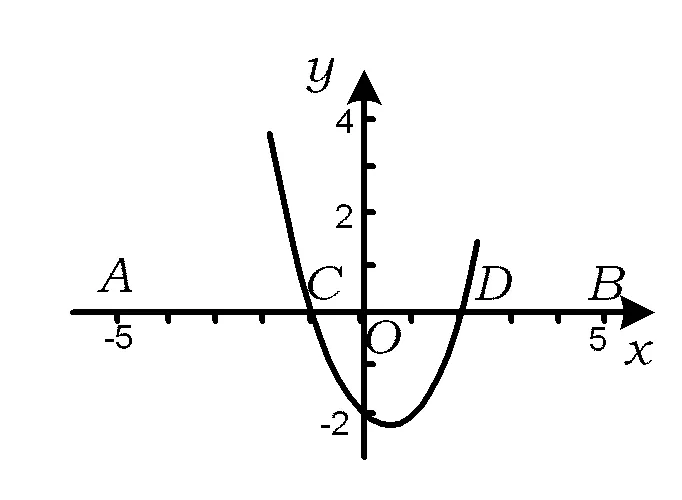
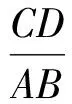
3 与方程相关的几何概型
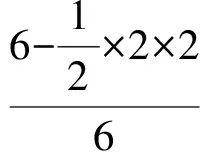
4 与不等式相关的几何概型

5 与平面几何相关的几何概型

6 与立体几何相关的几何概型

7 与解析几何相关的几何概型
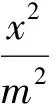
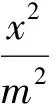

8 与算法相关的几何概型

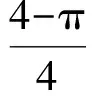
9 与集合相关的几何概型