集合论观点下的一类恒成立问题的辨析

● (三门教育局教研室 浙江台州 317100) ● (黄岩教育局教研室 浙江台州 318020)

集合论观点下的一类恒成立问题的辨析

●祝敏芝(三门教育局教研室 浙江台州 317100) ●洪秀满(黄岩教育局教研室 浙江台州 318020)

集合论是19世纪德国数学家康托(Cantor)创立的，现在已发展为独立的数学分支，其基本概念与方法已渗入到数学的各个领域，成为现代数学的基石.对于含有存在量词的存在性问题与含有全称量词的恒成立问题，本文试用集合论的基本概念与方法对恒成立进行辨析，挖掘这类问题的数学本质，让其思想更深刻，形式更简约.

1 问题的提出

笔者在一次听课过程中听到授课教师讲解了这样一道题目.

授课教师是这样讲解的：原不等式可化为

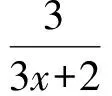
即

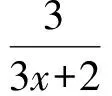
分离变量得

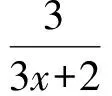
对不等式右边求导数确定单调性，于是

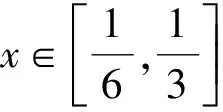
2 集合论观点下的命题辨析

逻辑词“或”给问题带来了复杂性，求交集与并集的运算顺序很容易混淆.如果用集合表示命题的外延，用集合的交、并运算表示命题转换，问题的数学本质就会变得清晰.

我们对这个式子作如下的变式：

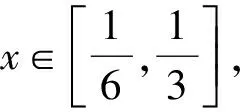
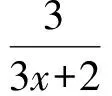
成立,求a的取值范围.

分析不等式可化为

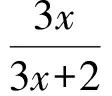
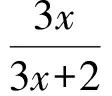
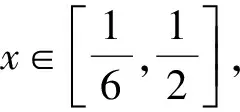
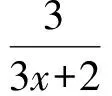
成立,求a的取值范围.

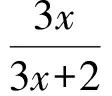
对于带有逻辑词的、较为复杂的恒成立命题，集合论观点下的辨析会使得问题清晰、明了.

3 集合论观点解决恒成立与存在问题的普适性

康托成功地运用集合对应计数的思想，通过将自然数集与有理数集中元素建立一一对应的方法，说明这2个集合有相等的势.同样地，对于集合之间的包含关系，运用集合对应思想分析就会有高屋建瓴之感，轻松地对问题建立深层次的理解.

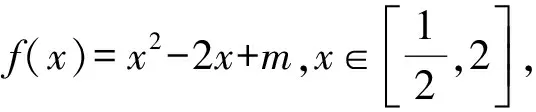
对于第(1)小题，区间[m-1,m]中有一个元素为0，即

0∈[m-1,m]，

得

0≤m≤1.

对于第(2)小题，区间[m-1,m]中的所有元素都大于0，即m>1.

例3已知函数f(x)=x3-(k2-k+1)x2+5x-2，g(x)=k2x2+kx+1，其中k∈R．

(1)设函数p(x)=f(x)+g(x),若p(x)在区间(0,3)上不单调，求k的取值范围.

(2009年浙江省数学高考试题)

若运用集合对应思想分析，则能使问题变得简单、明了.

当x<0时,

q′(x)=f′(x)=3x2-2(k2-k+1)x+5,

易知q′(x)在(-∞,0)上单调递减；

当x>0时，

q′(x)=g′(x)=2k2x+k，

q′(x)在(0,+∞)上单调递增．

对于任何一个x1>0的函数值q′(x1),都有一个x2<0的函数值q′(x2)与之对应，那么q′(x)在(0,+∞)上的值域是q′(x)在(-∞,0)上的值域的子集．反之，q′(x)在(-∞,0)上的值域是q′(x)在(0,+∞)上的值域的子集．

记q′(x)在(0,+∞)上的值域为A=(5,+∞)，q′(x)在(-∞,0)上的值域为B=(k,+∞)．由集合的相互包含,可得k=5；另一方面，当k=5时,A=B，则对任意x1<0，q′(x1)∈B=A,即存在x2>0,使得q′(x2)=q′(x1)成立.因为q′(x)在(0,+∞)上单调递增，所以x2的值是唯一的.同理，对任意x1<0，即存在唯一的非零实数x2(x2≠x1)，要使q′(x2)=q′(x1)成立，故k=5满足题意．

对于恒成立与存在性问题，我们一直自觉或不自觉地用集合思想进行分析，直觉的东西遇到复杂的问题会受阻碍.本文是从形式逻辑上归纳了这类问题的解题思路，首先用集合表示命题的外延，然后用集合的交、并、补运算表示命题转换，或者用集合对应计数思想表示命题之间的包含关系.可以说，集合论观点辨析恒成立问题充分凸显了数学的精确之美、简约之美.