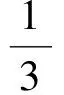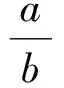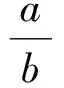线性规划在求解不等式范围问题中的应用

●

(武陟县第一中学 河南武陟 454950)

线性规划在求解不等式范围问题中的应用

●王雷义

(武陟县第一中学 河南武陟 454950)

不等式范围的求解是一个重点内容，在利用不等式性质求解不等式的范围时，要正确理解其性质，切不可盲目滥用，应注意不等式的应用方向.在解题过程中，有时会出现似乎可以运用不等式性质解题，且出现范围扩大、性质失效的现象.如果能够转换思路，利用数形结合的方法求解，往往可以避免错误的发生，从而达到求解的目的.因此用线性规划解决这类问题显然是一种比较好的方法，下面就这个问题略举几例说明.

例1已知函数f(x)=ax2+bx，1≤f(-1)≤2，2≤f(1)≤4，求f(-1)的取值范围.

解法1利用不等式的性质求解.

错解因为f(-1)=a-b，f(1)=a+b,所以由题意得

由不等式组利用不等式性质进行加减消元得

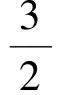
从而由f(-2)=4a-2b,可得

3≤f(-2)≤12.

错因分析不等式的性质除了个别外，其他的条件和结论间都不是充要条件，而只是充分条件.在解题中，使用性质定理，尤其是反复使用性质定理会使求解的范围扩大、变量的范围扩大，从而出现增根.本题正是因为多次利用了不等式性质中的加法法则(同向可加性)，而此法则是单向的，不具有可逆性，从而使a,b的范围扩大，这样f(-2)的范围也随着扩大了.

因为a-b,a+b中的a,b不是独立的，而是相互制约的，所以若将f(-2)用a-b和a+b表示，则问题可以得解.

正解设f(-2)=xf(-1)+yf(1)(x,y为待定系数)，则

4a-2b=x(a-b)+y(a+b)，

即

4a-2b=(x+y)a-(x-y)b.

于是

x=3,y=1,

从而

f(-2)=3f(-1)+f(1).

由题意

1≤f(-1)≤2,2≤f(1)≤4,

可得

5≤3f(-1)+f(1)≤10,

故

5≤f(-2)≤10.

点评严格依据不等式的基本性质和运算法则，是正确解决此类题的保证.

如果利用数形结合的方法解题,那么线性规划就不失为一种绝妙的好方法.

解法2利用线性规划求解.

建立线性约束条件，由1≤f(-1)≤2，可得

1≤a-b≤2；

由2≤f(1)≤4，可得

2≤a+b≤4.

因此可得线性约束条件不等式组

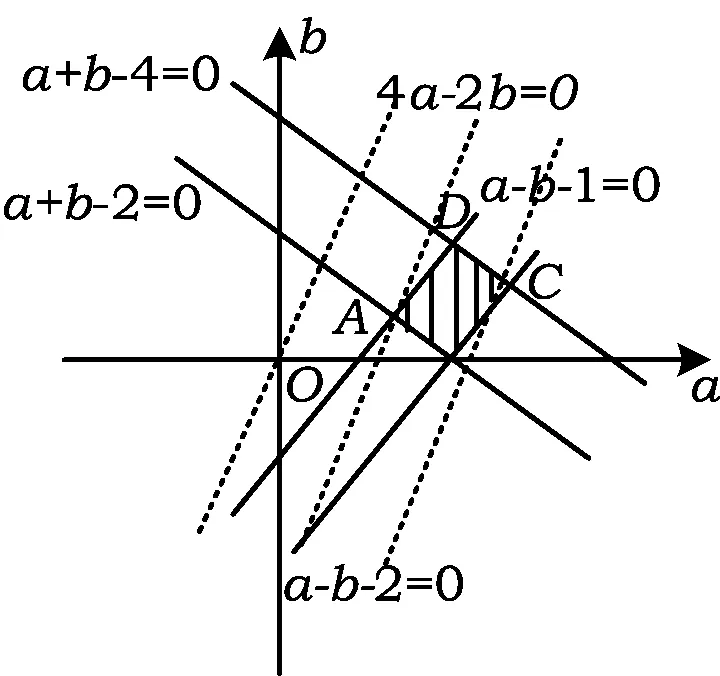
图1

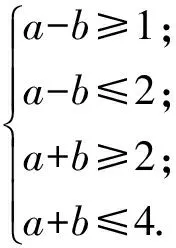
线性目标函数为f(-2)=4a-2b，如图1所示，过点(0，0)作直线l0:4a-2b=0.把直线l0向右下方平行移动到位置l′时，直线经过点A，此时f(-2)=4a-2b取得最小值.解方程组

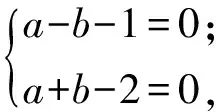
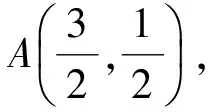
f(-2)min=5.

把直线l0向右下方平行移动经过点C，此时f(-2)=4a-2b取得最大值.解方程组

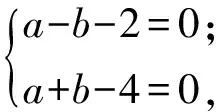
f(-2)max=10,

故

5≤f(-2)≤10.

点拨通过线性规划求f(-2)的最大值和最小值,避免了反复使用性质定理而导致范围扩大，出现增根的现象，结果直观明了，不易出错.

解法1利用不等式的性质求解.

从而

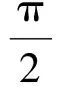
又由α<β，可得

山水集团单笔债券未按时兑付直接导致其他债务交叉违约,不但会影响到债券市场正常的运行秩序，还会对市场参与主体和投资者的切身利益以及中介机构的信誉带来较大的影响。另外，商业银行的贷款也会由于其资金紧张，安全性难以保障。一旦出现贷款违约后，又会引起债权银行提前收回贷款，进一步加剧了企业兑付债券的难度。如企业资金链断裂，最后可能出现债权银行和债券持有人权益同时遭受较大损失的局面。

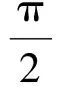
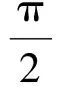
解法2利用线性规划求解.

建立线性约束条件，由题意可得不等式组

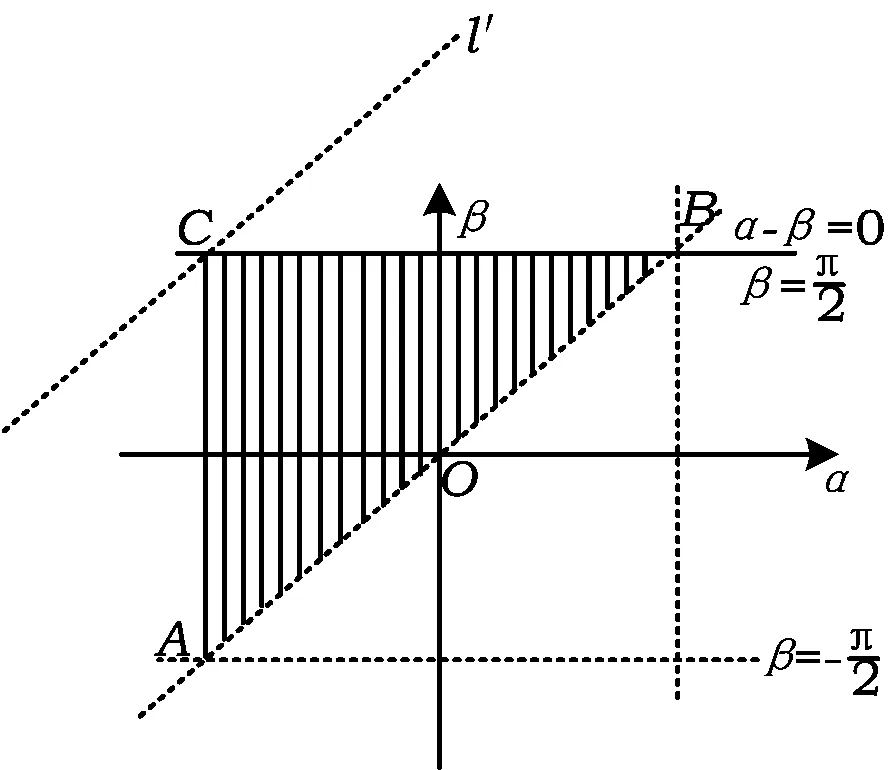
图2

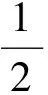
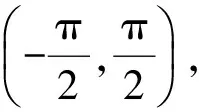
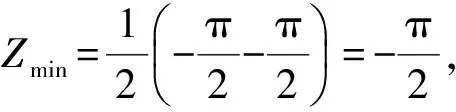
得

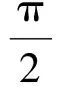
即

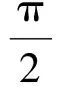
点评利用线性规划解答此题，条理清晰，简单明了.

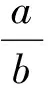
思维导引由题目可获得的信息是：利用已知条件(字母的取值范围)求代数式的范围.

本题可利用不等式的可加性和可乘性求解.

解法1利用不等式的性质求解.

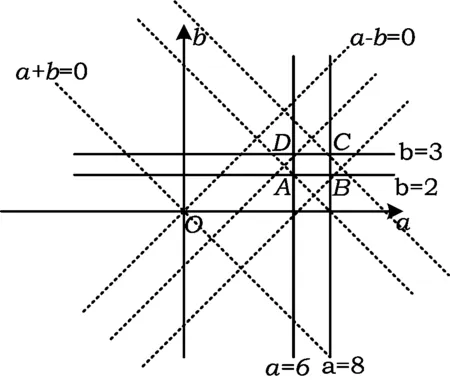
由6

8

因为-3<-b<-2,所以

3

解法2利用线性规划求解.

建立现行约束条件.由题意可得不等式组

图3

(1)如图3,作直线a+b=0,把直线a+b=0向右上方平移经过点A(6,2)，取得最小值，即

Zmin=6+2=8，

经过点C(8,3)取得最大值，即

Zmax=8+3=11,

所以

8

(2)

作直线a-b=0，把直线a-b=0向右下方平行移动经过点D(6,3)，取得最小值，即

经过点B(8,2)取得最大值，即

所以

3

点评本题用线性规划求解不如用不等式性质求解简单，但也体现出以数变形的直观性，再次说明了线性规划在解决不等式范围问题中的优越性.

华罗庚曾说过：“数缺形时少直观，形少数时难入微.”数形结合思想的妙处对于求解不等式范围问题中同样起着重要作用.我们知道，函数图像和不等式有着密切的联系,因此利用数形结合可以使问题直观明了，从而更能形象地解决问题.

不等式问题因其覆盖知识点多，方法也多种多样，但其核心思想还是等价转化.抓住了这点，才能以“不变应万变”，当然这还需要我们不断地去领悟、体会和总结.