基于粗糙集理论的法兰螺纹连接预紧状态研究

栗明燕 赵登峰 曾国英 张 言

基于粗糙集理论的法兰螺纹连接预紧状态研究

栗明燕 赵登峰 曾国英 张 言
(西南科技大学制造科学与工程学院，四川621010)

在法兰螺纹连接结构振动分析实验的基础上，引入粗糙集理论。对实验数据进行时域统计分析，得到响应信号的有效值、方差、偏斜度、峰度以及基座传感器的振动实验的响应信号作为基准求取基座响应信号与各传感器采集信号的相关度。由所得时域统计特征量建立判定法兰螺纹连接状态的信息系统，由粗糙集理论分析表明：偏斜度、峰度和相关度三个特征量可以完全判定螺纹的松紧程度，为连接状态的判断提供了依据。

粗糙集；螺纹连接；振动测试

粗糙集(Rough Set RS)理论是波兰学者Pawlak Z在1982年[1]提出的。它根据一个系统观察和测量所得的现实数据，从分类的观点，以集合近似、近似分类与不可分辨性等概念为基础，通过粗糙集理论简化方法，从中发现、推理知识和分辨系统的某些特点、过程，预测系统的结果等[2]。

1 粗糙集理论的主要概念

1.1 知识、论域与不可分辨关系

粗糙集理论的观点是“知识就是一种对对象进行分类的能力”，这里的“对象”是指我们所能言及的任何事物。也就是说，知识必须与具体或者抽象世界特定的语境相关的各种分类模式联系在一起，这种特定的语境称为论域[3]。给定一个论域U和U上的一簇等价关系S，若P⊆S，且P≠Q，则∩P是论域U上的一个等价关系，称为P上的不可分辨关系，记为IND(P)。

1.2 粗糙集合的下近似、上近似和边界区域

给定知识库K=(U，S)，其中，U为论域，S表示论域U上的等价关系簇，则∀X⊆U和论域U上的一个等价关系R∈IND(K)，我们定义子集X关于知识R的下IND(K)近似和上近似分别为：

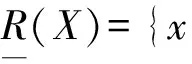
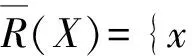
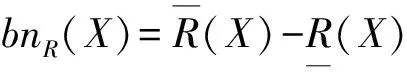
1.3 知识的表达系统和决策表

知识表达系统被看成一个关系数据表，关系表的行对应要研究的对象，关系表的列对应对象的属性，对象信息通过指定对象的各属性值来表达。具有条件属性和决策属性的知识表达系统称为决策表。设DT=(U，C∪D，V，f)是一个决策表，其中C和D分别为条件属性和决策属性集。

1.4 依赖度和约简

从图4可以看出，随着钢箱梁长度的增大，截面3所受弯矩呈现先减小后增大的趋势；钢箱梁长度由56 m增长到96 m时，截面3的弯矩减小幅度分别为17.5%、13.8%、11.5%、10.8%；钢箱梁长度由96 m增长到116 m时，截面3的弯矩减小幅度仅为2.4%、1.0%；钢箱梁长度由116 m增长到126 m时，截面3所受弯矩增长2.5%。

给定一个知识库K=(U，S)，∀P，Q∈IND(K)，定义：

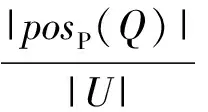
γP(Q)为知识Q依赖于知识P的程度。当γP(Q)=k=1时，称知识Q完全依赖于知识P，或称Q是由知识P导出的。当0<γP(Q)=k<1时，称知识Q完全依赖于程度k，粗糙依赖于知识P。给定一个知识库K=(U，S)和知识库上的一簇等价关系P⊆S，对任意的G⊆P，若G满足G是独立的且IND(G)=IND(P)，则称G是P的一个约简。

1.5 连续属性的离散化

粗糙集只能处理离散属性的数据，所以必须对原始故障诊断决策系统中的连续属性值进行离散化处理。常用的数据离散化的方法是：Naive Scaler算法对每个属性，按照属性值由小到大的顺序对决策表中的实例进行排序、判断，对于两个相邻实例，在属性值和决策值都不同的情况下，选取两个属性值的平均值作为断点值。这种算法不需要额外的参数，能够按照信息系统或数据库本身进行离散化。

2 螺栓连接实验及特征量的提取

2.1 螺栓连接状态的振动实验

判断螺栓连接状态的实验振动系统由法兰螺栓连接结构模型、振动台、传感器、数据采集卡、功率放大器和分析计算机组成。螺栓连接结构模型如图1所示。

图1 法兰螺栓连接结构模型Figure 1 Flange screwed connection structure model

实验中采用的螺栓连接结构模型主要由上下壳体两部分组成，材料为Q235。上下壳体通过法兰螺栓连接，法兰盘上均布有8个8.8级M6×25螺栓。经实验测定法兰螺栓连接结构的一阶固有频率为989Hz，二阶固有频率为1 838Hz，三阶固有频率为2 329Hz。

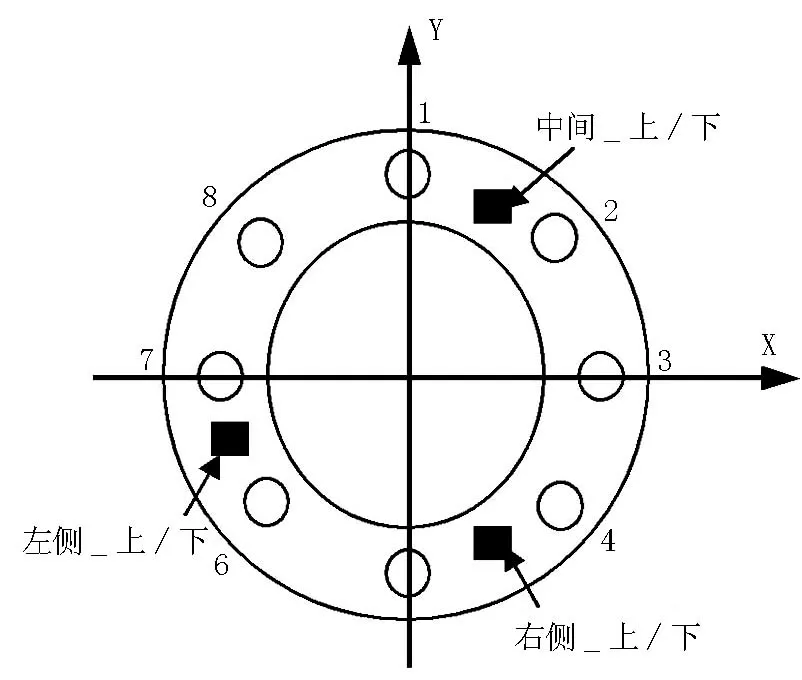
图2 螺栓的编号和传感器的布置Figure 2 Bolt number and sensor arrangement

2.2 特征量的提取

在实验中采用由Labview编程实现的200 Hz～3 000 Hz的平直谱伪随机信号作为振动实验的激励信号，激励信号的强度为0.5 V。改变螺栓的预紧状态，分别在预紧力矩(N·m)为0、1、2、4、5、6、7、8、9、10下进行振动实验，采集实验的响应信号。设定采样频率为100 kHz，一次实验采集得到的数据量庞大，其中存在大量的冗余。为剔除其中的冗余数据，减少计算量，对采集得到的响应信号做时域分析，分别求得响应信号的有效值、方差、偏斜度、峭度并以基座传感器的振动实验的响应信号作为基准求取基座响应信号与各传感器采集信号的相关度。定义螺栓在(0～3)N·m力矩时为松动状态、(4～6)N·m力矩时为预松动状态、(7～8)N·m力矩时为可接受状态、(9～10)N·m力矩时为紧密连接状态。

3 应用粗糙集理论对实验得到的数据进行分析

取实验中所采集的50组数据作为研究的对象，即论域U={x1，x2，x3，…，x50}，设U={x1，x2，x3，…，x49，x50}={1，2，3，…，49，50}。判断法兰螺纹连接结构的特征量即条件属性集C={有效值，方差，偏斜度，峰度，相关度}，设C={a,b,c,d,e}。需要判定的螺纹的连接状态即决策属性集D={松动，预松动，可接受，紧密连接}，设D={0，1，2，3}。

下面分4个步骤进行试验分析：

步骤1，由实验采集得到的数据建立判定法兰螺纹连接状态的信息系统，如表1所示。

表1判定法兰螺纹连接状态的信息系统

Table1Informationsystemofflangescrewedconnectionstatedetermination

步骤2，数据的离散化。选择Naive Scaler算法对连续属性离散化并在波兰华沙大学与挪威科技大学联合开发的Rosetta软件[4]中实现。

步骤3，决策表的知识约简。采用遗传算法对决策表的属性进行知识约简可得a和b属性是冗余的属性。删除这两个属性对于决策没有影响。

步骤4，分析得到的结果。由决策表可得：条件属性{c}对于决策0、1、2、3的下近似为

{{27}，{22}，{17}，{24}，{19}，{29}，{20}，{25}，{30}}；

{{27}，{22}{17}，{24}，{19}，{29}，{20}，{25}，{30}}，{18}，{28}，{23}，{16}，{21}，{26}}；

{{32，37}，{39}{34}，{40}，{35}，{33}，{38}，{36}，{31}}

同理可得到{d}、{e}、{c,d}、{c,e}、{d,e}以及{c,d,e}属性分别相对于决策属性0、1、2、3的下近似，由于篇幅关系不再一一例举。

由计算得到的下近似及知识的依赖度公式可分别计算属性集{c}、{d}、{e}、{c,d}、{c,e}、{d,e}和{c,d,e}相对于决策属性0、1、2、3的知识依赖度。各条件属性对决策属性的知识依赖度如表2所示。

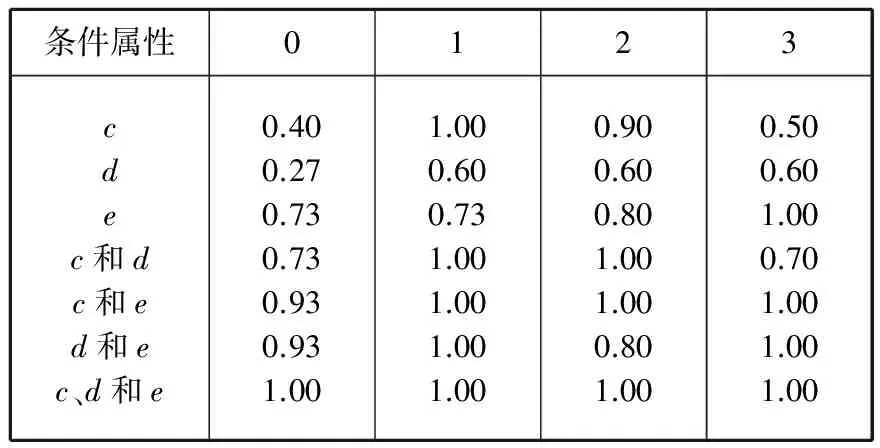
表2 各条件属性对决策属性的知识依赖度

分析可得：(1)在进行知识约简之前共5个特征量，应用遗传算法进行约简之后约去a和b两个属性。这个结果表明在时域分析时选取的5个特征量中有两个特征量是冗余的，去掉这两个特征量不会影响对螺栓连接状态的准确判断。(2)对剩余的条件属性组成的条件属性集分别计算其对决策属性的知识依赖度，计算的结果表明只有{c,d,e}对所有决策属性的知识依赖度均为1，即只有条件属性集{偏斜度，峰度，相关度}能准确的反应螺栓连接结构的连接状态。

4 结论

螺纹连接状态的判定是一个复杂的信息融合过程，各连接状态的特征量之间具有冗余性。本文将粗糙集理论应用于决策表的化简和故障特征数据的压缩。分析结果表明将选取的有效值、方差、偏斜度等5个属性量减少为3个，减少了40%的计算量。实验中改变螺栓连接预紧力矩时会存在误差，同时连接状态是连续量，将其转换为符号量会出现临界问题，造成分类错误或者误判，解决这些问题是下一步的工作重点。

[1] Pawlak Z.Rough sets.International Journal of Information and Computer Science,1982，(11)：341-3565 Pawlak Z.Vagueness and uncertainty-a rough set perspective.Computa-tional Intelligence，1995，11(2)：227-232.

[2] 兴连国，许宝杰.基于粗糙集对旋转机械故障诊断系统的研究.北京机械工程学院，2006，21(2)：5-8.

[3] 苗夺谦，李道国.粗糙集理论、算法与应用.北京：清华大学出版社.

[4] 吉增瑞.操作系统的并行处理.计算机世界，1996.

[5] 钟秉林，黄仁.机械故障诊断学.北京：机械工业出版社，2007.

[6] 李舜酩，李香莲.振动信号的现代分析与应用.北京：国防工业出版社，2008.

Research for Flange Screwed Connection Prefastening State Based on Rough Set Theory

QinMingyan,ZhaoDengfeng,ZengGuoying,ZhangYan

Rough set theory is introduced by analyzing the vibration experiment of flange screwed connection. Test data are statistically analyzed in time domain in order to obtain effective value, variance, skewness and kurtosis of response signal and vibration experiment response signal for foundation sensor as the reference to get the correlation between foundation response signal and various sensor collection signals. The information system of flange screwed connection state is established by the time domain statistics characteristic quantity. The rough set theory shows skewness and kurtosis and correlation can determine the fastening degree of screw thread completely which provide reference for connection state judgement.

rough set; screwed connection; vibration test

TB123

A

2010—06—04

栗明燕(1986—)，女，硕士研究生，研究方向为振动与测试。

国家自然科学基金和中国工程物理研究院联合基金资助项目(项目编号：10876034)。

编辑 杜青泉