基于平衡盘的双面在线动平衡系统原理与问题探析

张仕海 伍良生 周大帅 李 俊

(①北京工业大学机械工程与应用电子技术学院，北京100022；①天津海运职业技术学院，天津 300457)

旋转机械广泛应用于电力、石化、冶金、航空、航天、机械制造等部门。旋转机械设备的过大振动将导致噪声过大，降低工作效率，引起配合松动和元件断裂，进而引发事故的发生。据资料统计，旋转机械由于振动原因导致设备失效的大约为60% ～70%，其中由于转子不平衡失效的比例为30%左右［1］。可见，开展对高速精密转子系统平衡理论和技术的研究、开发高精度全自动的动平衡系统，对提高高速精密旋转机械的加工和运行质量等方面具有重大意义。

转子动平衡技术通常分为工艺动平衡、现场动平衡和在线动平衡。在线动平衡具有避免频繁开关机，提高平衡效率和精度，同时可实现旋转机械工作过程中的自动平衡等优点［2］。因此在线动平衡具有其它平衡方法不可替代的优势。从动平衡方法提出至今，国内外研究人员在此领域进行了大量的研究。本文在对盘式动平衡装置进行分析的基础上，提出几点结构问题及设计方法，并通过实例分析了该方法的平衡效果及优化选择的实现。

1 双平面影响系数法在线动平衡理论

设刚性转子的两支承面分别为A、B面，平衡校正面分别为Ⅰ面和Ⅱ面。当两校正面的校正量为零时，设在平衡转速上测得A、B面初始不平衡振动分别为

当在校正面Ⅰ上施加不平衡量为P1，Ⅱ面校正量为零，则平衡转速上测得A、B面振动分别为

则校正面Ⅰ对A、B面的影响系数分别为

当在校正面Ⅱ上施加不平衡量为P2，Ⅰ面校正量为零，则平衡转速上测得A、B面振动分别为

则校正面Ⅱ对A、B面的影响系数分别为

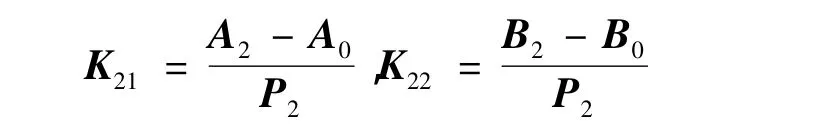
设欲将原始不平衡量引起A、B面的振动平衡掉，需在Ⅰ、Ⅱ面施加的校正量分别为Q1和Q2。则Q1和Q2满足方程：

根据Q1和Q2的计算结果，并在校正面Ⅰ、Ⅱ上施加对应大小的不平衡量，理论上可将A、B面的振动消除。

2 基于平衡盘的转子双面在线动平衡系统原理与构成

2.1 不平衡量的合成

正常运转时，平衡盘通过牙签形齿与啮合齿座(与主轴固定，如图1b)啮合，以防止平衡盘相对主轴的径向滑移。同时通过弹簧片的压力防止平衡盘轴向滑移。当平衡盘相对主轴基准的相位需要调整时，由驱动机构克服弹簧弹力使平衡盘与主轴脱离，通过平衡盘与主轴的差速运动或其它驱动机构实现平衡盘位置的调整。位置调整后，撤销驱动力，平衡盘在弹簧片弹力作用下重新与主轴啮合，同步运转。两平衡盘在一个平面内不平衡量的合成如图1a所示。设两平衡盘的不平衡量大小相等，则由图中几何关系可知：

式中：A为平衡盘与主轴同步旋转所产生的不平衡量大小；β，α分别为两平衡盘相对主轴基准的相位；P为全成的不平衡量大小，其相位为(β+α)/2，当β-α＜180°时取正，当 β-α ＞180°时取负。

设，计算所得某平面所需施加不平衡量为Q=q∠φ，则由方程

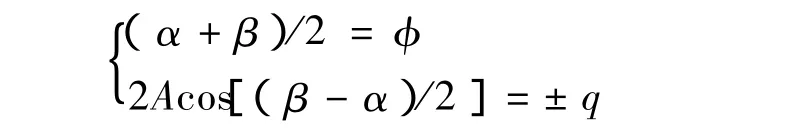
可计算出β及α的大小。即为平衡盘相对主轴基准的径向位置。

2.2 系统构成

根据双平面影响系数法的基本原理，可采用4个平衡盘，两两组合，配以相应的检测、控制、执行系统等，可以实现刚性转子的双平面在线动平衡。其系统构成如图2所示。

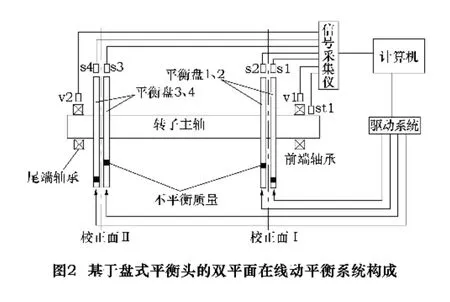
正常情况下，两平衡盘均与主轴啮合，同步运转。电涡流传感器v1，v2分别测取前后轴承的振动位移信号；光电传感器s1、s2、s3、s4用于监测4个平衡盘位置信号；光电传感器st1作为基准信号。各传感器测量信号经信号采集仪进行初步处理(A/D转换，电荷放大，低通滤波等)送入计算机在线动平衡测量、分析与控制系统软件。计算机对实时监测信号进行分析。当v1、v2检测的不平衡振动量超过允许范围时，计算机控制系统根据双平面影响系数法计算Ⅰ、Ⅱ面的不平衡校正量及对应平衡盘的位置，输出控制信号，经驱动系统对各不平衡盘位置进行调整。当s1、s2、s3、s4监测的位置信号达到调整位置时，撤销驱动力，各平衡盘重新与主轴啮合，系统重新进入监测与控制状态。

3 平衡盘的结构问题分析

3.1 实验数据来源

为对系统的结构、平衡效果及优化等方面的问题进行分析和设计，这里采用文献［3］中的部分实验数据进行相关的计算和分析。选取数据如表1所示［3］。其中最大振幅量为原始实验数据，影响系数为笔者计算数据。

表1 参考数据

3.2 平衡盘与主轴啮合齿距的问题

基于以上理论可知，根据实际监测的不平衡振动量的大小和相位，利用双平面影响系数法可以计算出在Ⅰ、Ⅱ平面上需要施加的不平衡量大小和相位。通过4个平衡盘相位的调整，即可实现Ⅰ、Ⅱ平面上需要施加的不平衡量大小和相位的要求。然而，在对平衡盘位置进行调整时，由于受齿距的限制，平衡盘位置只能调整到某些确定的位置。如，当啮合齿圆有72个齿时，平衡盘可达到 0°，5°，10°…355°共 72 个位置。因而产生平衡盘的实际位置与理论计算位置之间的误差。齿距越小，平衡盘的实际位置与理论计算位置的误差越小，平衡精度越高。然而，齿距越小，加工越困难，同时容易产生齿断裂等故障。需综合考虑设计以后分析采用72齿结构，平衡盘角度最大调整误差为2.5°。

3.3 平衡盘不平衡质量的选取

由2.1不平衡量合成原理可知，平衡盘不平衡质量的大小对系统的平衡效果影响较大。质量太小，不足以将测点的不平衡振动平衡掉；质量太大，合成不平衡量对平衡盘角度调整误差较敏感，当角度调整误差较大时，平衡效率较低。可以在设计阶段通过试重实验求出影响系数，然后对不同质量的平衡效果进行理论计算，最终设计出较理想的不平衡质量。表2为在表1影响系数的基础上，不同的不平衡质量对三次实验平衡效果的计算。

表2 平衡盘不平衡量大小对平衡效果的影响计算

表3 对测点1优化前后平衡效率比较

由表2可以看出，随测点1、2不平衡振动的改变，理论上均能达到较好平衡效果的平衡盘不平衡质量为5 g，其理论计算平衡效果均达95%以上。

4 双平面在线动平衡的单点优选问题

以上分析表明，平衡盘可达到位置与理论计算位置之间存在偏差。进而理论上不能将测点的不平衡振动完全平衡掉。然而，在实际应用中，并不一定要求每一点的平衡效果均能达到最佳，而是对某些关键部位的不平衡振动比较关注。例如某部位的附件较多，振动对系统的性能影响较大；某部位结构相对薄弱，振动对部位损坏较大；机床主轴前端夹装刀具，振动对工件的加工精度、表面质量影响较大等。针对这些情况，可以考虑在其它测点的振动不超过某一极限的情况下，使关键部位测点的不平衡振动尽可能的小，即刚性转子双平面动平衡的单点优选问题。一种优选方法是采用某种查找方法，针对4个平衡盘位置的不同组合进行计算，查找符合要求的最佳位置。如果每个平衡盘有72个位置，4个平衡盘的不同组合达2600多万种，查找和计算的时间较长，不适合快速平衡的要求。笔者将多篇文献中的相关数据，分别采用以上方法查找计算，实践表明，单点优选后，平衡盘的最佳位置均处于理论计算值±50°的范围内。以此为依据，可使查找的范围大大缩小，实现快速平衡。表3、4为平衡盘不平衡量为5 g，对测点1优选的结果。

表3的理论计算表明，在刚性转子双平面影响系数法动平衡技术的基础上，采用单点优选的方法可以提高转子系统中某些关键部位的平衡效果，同时其它部位的动平衡效果也可以保持在一定的水平。进而提高整个转子系统的工作性能。

5 结语

(1)采用盘式平衡头的转子动平衡系统具有结构简单，轴向尺寸小，在旋转机械上容易实现等优点。平衡盘上啮合齿的齿距越小，平衡盘的实际位置与理论计算位置的误差越小，平衡精度越高。然而齿距越小，加工越困难，同时容易产生齿断裂等故障，需综合考虑设计。

(2)平衡盘不平衡质量的大小对平衡效果的影响较大。质量太小，不足以将测点的振动平衡掉；质量太大，合成不平衡量对平衡盘角度调整误差较敏感，当角度调整误差较大时，平衡效率较低。可以在设计阶段通过试重实验求出影响系数，然后对不同质量的平衡效果进行理论计算，最终设计出较理想的不平衡质量。

(3)受齿距影响，平衡盘位置存在调整误差，难以保证各测点的平衡效果同时达到最佳。采用双面平衡、单点优选的方法可以提高转子系统中某些关键部位的平衡效果，同时其它部位的动平衡效果也可以保持在一定的水平。进而提高整个转子系统的工作性能。

［1］伍良生，贺江波，张云禧，等.高速主轴在线动平衡机构驱动器设计［J］.北京工业大学学报，2007，33(12)：1233-1238.

［2］欧阳红兵，曾胜，汪希萱.转子系统在线动平衡综述及展望［J］.机械强度，1997，19(4)：20-24.

［3］孙延添.刚性转子现场动平衡理论分析及实验研究：［硕士学位论文］［D］.北京：清华大学，2005(6)：46-50.

［4］叶能安，余汝生.动平衡原理与动平衡机.武汉：华中工学院出版社，1985.

［5］周保堂，贺世正，王宇，等.在线自动平衡的平衡头研究［J］.石油化工设备技术，1994，15(3)：42-45.