基于Deform 3D的高速超高速磨削温度的仿真研究*

沈琳燕 李蓓智 杨建国 冯瑞金 周振新

(东华大学机械工程学院，上海 201620)

磨削技术在材料加工中有着极其重要的地位，它不仅是大部分产品形成前的最后一道工序，而且随着磨削技术的飞速发展，磨削加工的能力和范围也正在日益扩大。超高速磨削是一种能高效、经济地制造高质量零件的现代加工技术，它可大大提高加工生产率和工件表面质量，并能实现粘性金属和脆性金属等难加工材料的精加工，大幅度缩短产品的生产制造周期，降低加工成本［1-3］。

但由于实际加工过程中的磨削温度、应力、应变等的测量极其困难，单纯依靠实验很难对磨削机理进行深入地研究。采用有限元法分析外圆磨削加工过程不仅有利于对磨削机理的理解，而且也是机械加工工艺优化的有利工具。与直接实验方法相比，该方法费用低，耗时短，在考虑多因素时其优势尤为显著，同时，随着计算机运算和视觉技术的发展，也必将促进虚拟加工的进一步发展［4-5］。

Liu等［6］对纳米结构涂层材料的微磨采用热弹塑性有限元方法建立了2D模型，指出磨粒切削作用和挤光效应是磨削后涂层中应力改变的主要原因；Hédi等［7］提出了AISI 52100钢磨削过程的有限元热力耦合2D 模型；STRENKOWSKI等［8］采用了基于 Eulerian的正交有限元切削模型与基于USUI的3D切削分析模型相耦合的方法，提出3D切削的预算模型；明兴祖等［9］采用PRANDTL-REUSS方法建立了应力应变场本构关系，构造了3D力热耦合磨齿模型。

本文运用商业化软件DEFORM-3D，针对工程常用材料40Cr钢进行了高速超高速磨削工艺仿真试验，对其砂轮线速度在60～210 m/s条件下的磨削弧区温度进行对比分析，揭示超高速磨削的磨削温度变化规律和机理，实现对工艺参数的优化选择提供理论依据。

1 有限元模拟的理论基础

1.1 J-C材料本构模型的建立

本文采用40Cr钢作为工件材料，并用Johnson-Cook(J-C)材料本构模型描述工件材料。J-C材料模型是一个能反映应变率强化效应和温升软化效应的理想刚塑性强化模型，该模型利用变量乘积关系分别描述应变、应变率和温度的影响。该模型具体表述式如下：式中：A、B、C、n、m分别为材料参数为量纲(应变率)为有效塑性应变率为参考塑性应变率，一般取=1 s-1；T*为量纲(温度)，T*=(T；Tr为参考温度；Tm为熔点温度；T为样品环境温度。

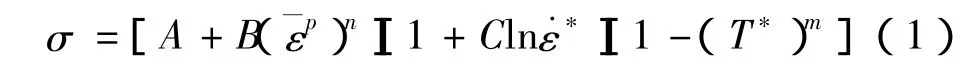
Johnson-Cook材料模型实际上给出的是von-Mises流动应力σe与等效塑性应变、相对等效塑性应变率和无量纲温度T*之间的函数关系。同时，给出了断裂应变的表达式。

1.2 自适应网格重划分技术

金属磨削过程可以看作是无数个微型刀具作切削加工，其形成过程即为工件产生塑性变形并发生切屑与工件的分离。所采用的有限元法主要有两种，即弹塑性有限元法和刚塑性有限元法。在工件尺寸、网格划分数量等条件相同的情况下，两者所得出的应力、应变、温度分析结果几乎相同。由于本文对工件加工后的残余应力和回弹问题不予研究，故采用刚塑性有限元模型即可，它的求解速度比弹塑性有限元模型快3～5倍。

采用刚塑性有限元模型(更新的拉格朗日方法)模拟磨削加工过程属于典型的几何非线性问题，同时还具有连续性和动态性的特征。随着磨粒与工件的接触，工件材料发生塑性变形，材料初始网格产生畸变、退化，这种网格的严重畸变会导致求解精度的降低或者计算不收敛。为了避免此种情况的出现，在有限元仿真过程中必须采用自适应网格重划分技术(Remeshing)。随着砂轮的进给，工件被加工部分实现网格细分，而没有加工的部分或者已加工部分，网格较粗，这样既保证了局部变形的求解精度降低问题，又节省了求解时间和内存的消耗。

2 有限元模型的建立

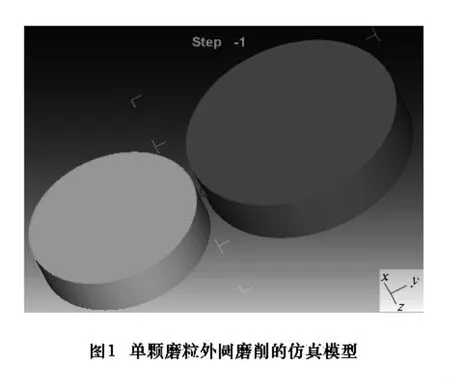
本文建立了基于单颗磨粒外圆磨削过程仿真的有限元模型，如图1所示。单颗磨粒以一定的速度与工件发生作用，在磨削区发生了复杂的物理、化学变化，工件产生了非线性的弹塑性变形。DEFORM-3D是一个基于工艺模拟系统的有限元系统(FEM)，可用于分析各种金属加工过程中的三维流动，提供极有价值的工艺分析数据，以及加工过程中的材料和温度流动。

2.1 几何模型的建立

在UG5.0中画出单颗磨粒的砂轮及工件的三维实体图，保存成.stl文件形式输出，在DEFORM-3D前处理中导入三维几何模型，其中Top-Die为砂轮，设置成刚性(rigid)；Workpiece为工件，设置为塑性(plastic)。为方便进行工件的前处理设置以及提高求解速度，在本研究中，取工件的1/4作为研究对象，如图2所示。

2.2 预处理设置

预处理设置作为加工仿真分析的准备工作，主要完成前处理设置、生成数据库和模拟运算三个步骤［10］。

在仿真控制(Simulation Control)中设置仿真步数为80步，时间增量为1×10-7s，存储增量为每2步保存一次，时间步长设置不能太大，否则会降低求解精度，导致网格严重畸变甚至不收敛。采用国标单位标准SI，仿真模式为热传递(Heat Transfer)和变形(Deform)；迭代方法(Iteration Method)采用 Direct iteration；求解器(Deformation Solver)采用共轭梯度法(Conjugate-Gradient Solver)，C-G 法为 DEFORM 3D中最常用的求解器，这种方法考虑了刀-屑之间的摩擦及工件材料流动应力受应变、应变速率和温度的影响。该方法对多数FEM问题都具有优势，但对于有些问题，如接触点较少的情况，收敛较慢甚至不收敛，此时，软件会自动识别转为Sparse法求解。因此，可有效的保证较少的迭代次数和迭代收敛性。

采用四节点四面体对工件进行网格划分，砂轮和工件均采用绝对类型，砂轮网格数5万，转动中心为(0，0，0)；工件网格数为20 万，材料为 DIN-41Cr4(相当我国标准40Cr)，工件材料预加工部分网格进行局部细化，最小网格单元为0.009 mm。工件的热传导率(Thermal Conductivity)如表 1 所示［11］。

生成数据库并完成模拟运算。

表1 工件的热传导率

3 仿真结果分析

3.1 磨削弧区温度分析

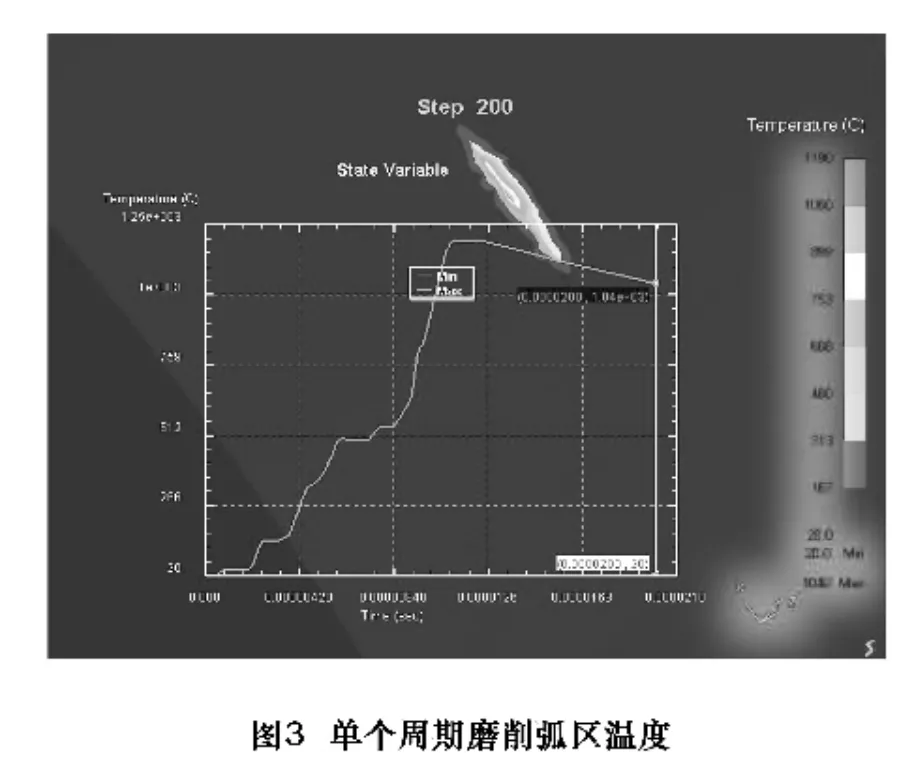
在磨削加工的仿真过程中，磨削弧区的温度、热流以及应力状态将会随着磨削的进行发生相应的变化。图3为单个周期内磨削弧区温度场的分布情况以及温度的变化规律。在磨削弧区的方向上，随着砂轮的旋转，磨粒逐渐切入工件，温度以极大的梯度上升，大约在弧区中心附近达到最大值(峰值达到1190℃左右)；之后随着磨粒的切出，切深逐渐变小，温度缓慢下降。这是由于在磨削过程中采用了干磨的方式，没有磨削液的冷却作用，产生的热量无法迅速耗散，工件表面温度将在短时间内处于较高状态，因此在实际生产过程中，磨削液的正确使用对磨削加工有着至关重要的作用。

3.2 磨削弧区热流分析

图4为磨削弧区热流的分布情况。可以发现沿着磨削弧区的热流并不是逐渐增加的，而是随着砂轮的旋转，单颗磨粒从开始接触工件到磨粒切出工件，产生的热流呈现出非线性的先上升后下降的规律。这是由于在磨削加工过程中，随着磨粒的切入，切深逐渐变大，随之产生大量的磨削热，大约在弧区中心位置产生最大热流，且热流分布形状可近似的看成二次曲线分布。

3.3 磨削弧区最高温度的变化规律

图5为不同砂轮线速度时，砂轮磨削工件时磨削弧区最高温度的变化情况。从图中可以看到，磨削弧区最高温度随着砂轮线速度的提高呈现先上升后下降的趋势，这是因为在速度较低时，磨粒主要以耕犁及滑擦作用进行磨削，此时摩擦加剧，产生热量增多，从而使磨削温度升高；当提高砂轮线速度至120 m/s后，使得未变形磨屑厚度减小，每颗磨粒切下的磨削层厚度变薄，有利于磨屑的形成排除，部分热量被磨屑带走，因而磨削区最高温度降低。

4 结语

(1)本文基于J-C材料本构模型建立了单颗磨粒磨削加工的三维有限元模型，采用更新的拉格朗日法和网格自适应技术成功的模拟了外圆磨削40Cr钢加工过程。

(2)采用有限元软件模拟磨削加工过程，分析磨削弧区最高温度的变化情况，减少研究中试切的实验次数，提高研究效率，降低研究成本，为实现对工艺参数的优化选择提供理论依据。

(3)分析了砂轮磨削工件过程中，磨削弧区温度和热流的变化规律，沿着磨削弧区方向，温度和热流从磨粒切入端到切出端呈现非线性的先增大，大约在接触弧区中心达到最大值，然后缓慢减小。

(4)分析了不同砂轮线速度下，磨削弧区最高温度的变化情况，温度随着砂轮线速度的提高呈现先上升后下降的趋势，高速磨削可以有效地防止工件烧伤。

［1］陆名彰，熊万里，黄红武，等.超高速磨削技术的发展及其主要相关技术［J］.湖南大学学报：自然科学版，2002，29(5)：44-48.

［2］KLOCKE F，BRINKSMEIER E，EVANS C，eta1.High-speed grinding fundament Ms and state of the art in Europe［ J］.Japan and the USA.Anrials of the CIRP，1997，46(2)：715-724.

［3］李伯民，赵波.现代磨削技术［M］.北京：机械工业出版社，2003：39-41.

［4］Domenico Umbrello，Finite element simulation of conventional and high speed machining of Ti6Al4V alloy［J］，Journal of Materials Processing Technology ，2008，196(1-3)：79-87.

［5］邓文君，夏伟，周照耀.有限元法在切削加工过程分析中的应用［J］.工具技术，2004，38(11)：20.

［6］Liu X B，Zhang B.Effect s of Grinding Process on Residual Stresses in Nanostructured Ceramic Coatings［ J］.Journal of Materials Science，2002 ，37(15)：3229-3239.

［7］Hédi H，Hassan Z，Jean-Michel B.Residual Stresses Computation in a Grinding Process［ J］.Journal of Materials Processing Technology，2004，147(3)：277-285.

［8］STRENKOWSKI J S，SHIH A J，LIN J C.An analytical finite element model for predicing three-dimensional tool forces and chip flow［ J］.International Journal of Machine Tool&Manufacture，2002，42(6)：723-731.

［9］明兴祖，严宏志，陈书涵，等.3D力热耦合磨齿模型与数值分析［J］.机械工程学报，2008，44(5)：17-24.

［10］李传明，王向丽，闫华军.DEFORM5.03金属成型有限元分析实例指导教程［M］.北京：机械工业出版社，2007.

［11］曾正明.机械工程材料手册(金属材料)［M］.北京：机械工业出版社，2003.