Weibull分布的若干性质

赵呈建，徐文青

(河南工程学院 数理科学系， 河南 郑州 451191)

在研究产品寿命以及断裂力学问题中，有很多随机变量都是服从Weibull分布的.通过对Weibull分布的讨论可以对这些随机变量的取值概率进行计算和推断，从而解决工程技术的相关问题.然而，Weibull分布不同于正态分布等常见分布，它是一类比较复杂的分布，在应用中具有一定的难度.要解决相关的问题，就必须计算出Weibull分布随机变量函数的分布.本研究从Weibull分布的性质讨论出发，给出了Weibull分布的一些常用函数的数字特征.

1 Weibull分布的定义与特征

1.1 Weibull分布的定义

定义1[1-2]如果随机变量T的分布函数F(t)为：

(1)

则称随机变量T服从Weibull分布，其中m>0，η>0，m叫形状参数，η叫刻度参数.这是两参数的Weibull分布，常记T～W(m,η).

Weibull分布形式类似指数分布形式，但比指数分布复杂得多.Weibull分布有三参数的分布详见参考文献[2].

由Weibull分布定义1知两参数Weibull分布的密度函数为：

(2)

1.2 Weibull分布两个参数与密度函数图像的关系

1.2.1 形状参数m

Weibull分布中形状参数m是最重要的参数，它的值决定了密度函数曲线的形状.当m=1时，Weibull分布就是指数分布；当01时，图像有一个峰，随着m>1的增大，峰值越高，图像越窄，见图1.

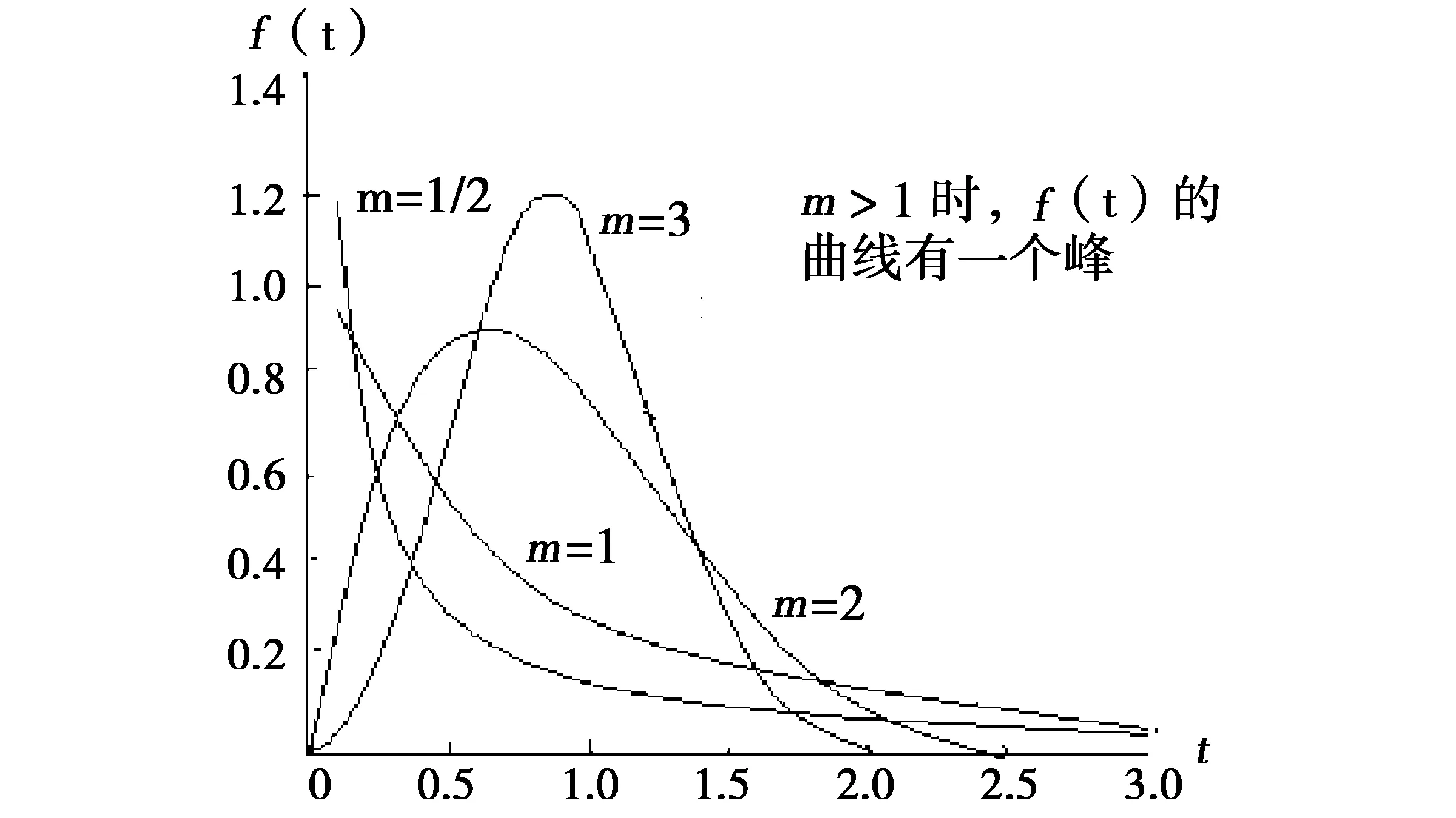
图1 形状参数对密度函数的影响Fig.1 The influence of shape parameter on the curve of density function

1.2.2 刻度参数η

对于刻度参数η，如果固定m，例如m=2，随着刻度参数η的增大，图像的峰值降低，图像变得偏平.图2是不同的η值密度函数图像的形状.

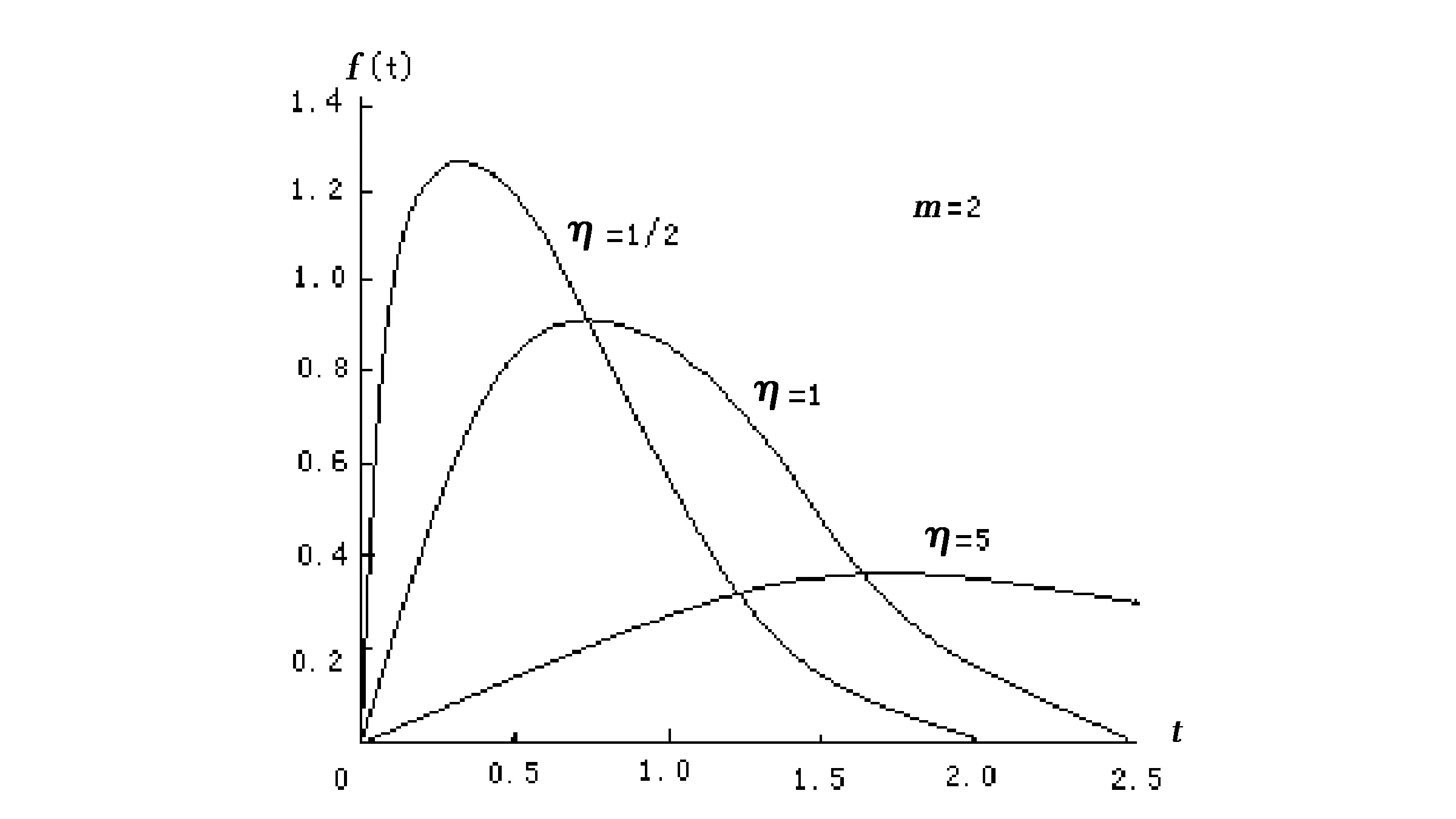
图2 刻度参数对密度函数曲线的影响Fig.2 The influence of scale parameter on the density curve

2 Weibull分布的性质

下面以定理形式给出关于Weibull分布的性质并加以证明.

2.1 Weibull分布常用的性质

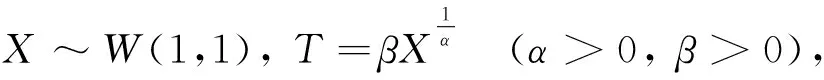
证明X～W(1,1), 即F(x)=1-e-x是指数分布(当m=1时Weibull分布是指数分布)，因此对任何t>0有

即T～W(α，β). 证毕.

定理1说明任何Weibull分布可以通过指数分布的变换得到.

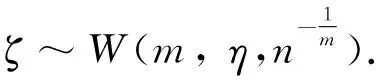
证明对任何t>0有

即

(3)

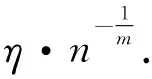
定理2是可靠性理论中的有名的夭折试验.

定理3 设T～W(m，η)，则X=lnT服从极值分布，其中参数

(4)

证明对任何t>0，有

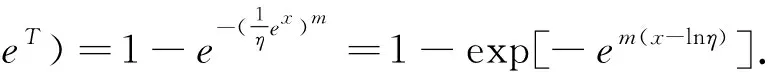
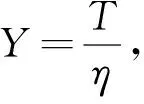
证明对任何t>0，有

定理4说明研究Weibull分布问题重点应放在对形状参数m的研究上.

E(lnkY)=Γ(k)(1)/mk.

其中，Γ(·)是Gamma函数，Γ(k)(·)是Γ(·)的k阶导数.

证明由数学期望定义和定理4知

令Z=Ym，则有

根据Gamma函数Γ(α)在域α>0内有各阶连续导数并且可在积分号下求导的性质[4]，有

当α=1时可得

E[lnkY]=Γ(k)(1)/mk,

(5)

结论成立.

用Ψ(z)(z>0)记Digamma函数[5]，其定义为：

γ是欧拉常数.

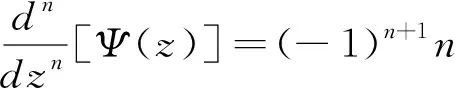
(n=1，2，3，…)

由上式以及Ψ(z)与Γ(z)之间的关系可求出Γ(k)(z)：

Γ′(1)=Γ(1)Ψ(1)=-γ，

(6)

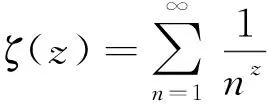
2.2 Weibull分布随机变量函数的数字特征

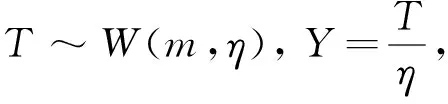
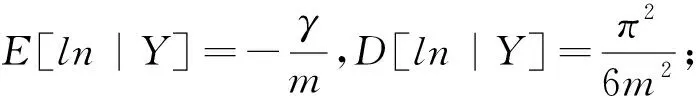
(7)

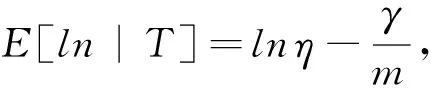
(8)

证明(1) 由定理5、(5)式及(6)式知

(2) 由数学期望和方差的性质知

T=ηY， lnT=lnη+lnY，那么

定理7 设T～W(m，η)，则有:

(9)

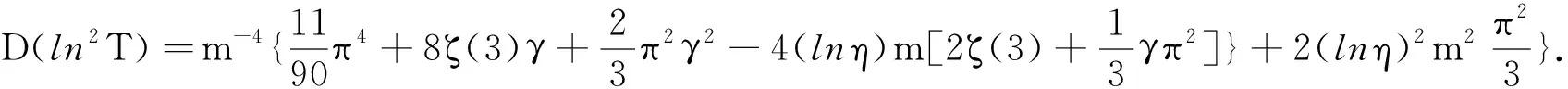
(10)

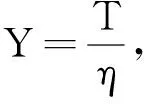
Cov[lnY，ln2Y]=E[ln3Y]-E[lnY]E[ln2Y]=

m-3Γ(3)(1)-m-1Γ′(1)·m-2Γ(2)(1)=

(11)

Cov[lnT，ln2T]=Cov[lnY+lnη，ln2Y+2lnηlnY+ln2η]=E{[lnY+lnη]·[ln2Y+2lnηlnY+ln2η]}-E[lnY+lnη].

E[ln2Y+2lnηlnY+ln2η]=

E[ln2Y]+3lnηE[ln2Y]+3ln2ηE[lnY]+ln3η-E[lnY]·E[ln2Y]-2lnηE2[lnY]-3ln2ηE[lnY]-lnηE[ln2y]-ln3η=

E[ln3Y]-E[lnY]·E[ln2Y]+2lnηE[ln2Y]-2lnηE2[lnY]=Cov[lnY，ln2Y]+2lnηD[lnY]=

对于(2)， 由定理5知

D[ln2Y]=E[ln4Y]-E2[ln2Y]=

m-4Γ(4)(1)-[m-2Γ(2)(1)]2=

(12)

D[ln2T]=D[(lnY+lnη)2]=

D[ln2Y]+4lnηCov[ln2Y，lnY]+4(lnη)2D[lnY].

由定理6、(11)、(12)和上式知(10)式成立，证毕.

3 结 语

本文重点讨论了Weibull分布两个参数与其密度函数的关系，并对常用的性质给予了详细的推导，特别导出了某些服从Weibull分布的随机变量函数的数字特征，为Weibull分布的应用打下了基础.

参考文献：

[1] 茆诗松，王玲玲.可靠性统计[M].上海：华东师范大学出版社 ，1984.

[2] 陈家鼎.生存分析与可靠性[M].北京：北京大学出版社，2005.

[3] 叶慈南.完全样本情形下Weibull分布的参数的估计[J].应用概率统计，2003, 19(3)：259-266.

[4] 格·马·菲赫金哥尔茨.数学分析原理[M].丁寿田译.北京：人民教育出版社，1979.

[5] 《数学手册》编写组.数学手册[M].北京：人民教育出版社，1979.