基于L1样条与B样条改进的利率期限结构估计优化

○吴泽福 吴 捷

(1. 华侨大学 工商管理学院, 福建 泉州 362021; 2. 澳门大学 管理学院, 中国 澳门)

一 引 言

利率期限结构是由特定时刻的到期期限与其对应利率的系列组成，而利率期限结构静态估计是指对特定时刻的利率期限结构进行数值估计，对发展和完善中国资本市场和和金融体制具有重要的理论意义和现实意义。利率期限结构是资产定价、风险管理和投资运作的基础，不仅直接影响公司投资决策和资金筹划，密切作用于国际经济贸易和宏观经济运行, 而且也是央行控制短期利率变化以影响中长期利率变化的传递机制。国内外大量研究表明，利率期限结构的变动规律能够比较全面地刻画资金市场的发育水平，综合反映经济增长预期、资金市场供求、宏观政策趋势和国民经济运行状况。

国际上利率期限结构静态估计模型已经从息票剥离法、多项式样条插值，发展到采用整条曲线拟合的Nelson-Siegel简约模型[1]473-489，以及采用分段曲线拟合技术的样条函数类方法,主要有McCulloch的三次多项式样条[2]19-31、Vasicek-Fong的指数样条及Steeley的B样条函数。线性内插式息票剥离法运用单变量求解进行运算产生的计量误差相对较小，但是有可能由于新发行债券收益率数据的到期缺口而导致不能够准确地描述即期利率函数的曲率，而Stephan发现立体样条保值式利息剥离法在降低了线性内插的估测误差的同时提供一个平滑的远期利率函数，但是存在估测结果相当敏感于节点的选择和在到期范围末尾会造成额外曲线曲率的严重问题。简约模型的优点是参数经济意义明确和所需估计的参数相对较少，缺点是需要预设部分参数来限定曲线类型,算法涉及非线性优化且收敛速度很慢，模型估计存在的系统化凹性影响到长期债券的定价精度。样条函数类方法对曲线拟合能力和适应性较强,程序估计误差易于控制和拟合结果稳定性较高，尤其是B样条函数的局部非零性质能够避免多项式样条估计方法中存在的回归矩阵多重共线性问题，但估计方法在样条函数以及分割区间上存在着较大的选择空间,需要运行标准定价误差的最小化搜索程序降低估计误差。Steeley得出B样条函数能够相当精确地近似贴现函数和获取平滑的即期利率曲线[3]513-529，Deacon和Derry通过比较各种拟合技术得出B样条函数是最有效的利率期限结构的估计方法。Fisher,Nychka和Zervos指出B样条函数法能够克服McCulloch使用平方样条拟合时产生的远期利率曲线的节点问题[4]85-116，但Chambers证实B样条函数拟合效果受到样本区间内节点选择的影响重大[5]233-252。指数样条克服多项式样条对拟合远期利率的不稳定性，能够较好地刻画利率到期期限延伸的拖尾曲线形状。Vasicek和Fong设定折扣函数形式上是指数衰减，避免了二项式样条函数不具有恒定的曲率而导致远期利率曲线斜率的近似误差问题，但Fong发现指数样条的期限结构拟合法有时劣于立体样条法，常用的三次指数样条函数系数需要利用非线性回归，所得的远期利率曲线不稳定且所需要计算量相当大[6]339-348。

国内学者采用不同方法构建利率期限结构，如陈雯和陈浪南采用指数函数,郑振龙和林海[7]33-36，朱世武和陈健恒，周荣喜和邱菀华采用多项式样条，谢赤和钟赞运用立方插值法，赵宇龄、范龙振和王晓丽采用Nelson-Siegel模型,朱峰采用带平滑技术的B样条，刘灿和易璐，傅曼丽、董荣杰和屠梅曾采用三阶B样条[8]1337-1340，大部分已有的利率期限结构实证研究偏重于函数构造及价格拟合度的验证,而忽视了最小化估计误差约束的拟合模型优化与整体估计效率分析以及现实市场上存在的诸多摩擦因素的影响。

本文的主要贡献体现为：(1)通过比较基本利率期限结构静态估计模式的优劣，推进B样条函数贴现拟合方法运用程序的优化研究；(2)构建B样条函数最小化定价误差的节点组合人工搜索程序，丰富了B样条函数估计在节点数目和定位的有效方式；(3)运用L1样条优化技术进一步放宽B样条函数对贴现函数的二阶平滑要求和克服对节点数目与定位的人工干预，增强了对当期价格变动特征的估计能力，深化了债券定价精确度和贴现函数过度波动问题的研究。本文的研究旨在改进利率期限结构静态估计方法的精确度，为利率期限结构动态机制研究提供精确数据，提升央行货币政策决策的有效性和科学性。

二 研究方法

1．B样条改进

(1)

(2)

(3)

(4)

运用此方法估计的贴现函数在到期时取值为1，不需要系数的约束条件。但是运用这种方法会导致短期利率的估计过度敏感于到期期限的改变，从而产生利率期限结构估计的不稳定，而且模型的估计需要运用到非线性估计技术。虽然运用样条函数可以直接拟合远期利率曲线，但是Bing和Huei指出此种方法所需要的计算量相当费时且估计获得的利率期限结构曲线末端相当不稳定，故而本文暂不采用此法。

2．L1样条技术[9]197-229

L1样条拟合方法放宽了贴现函数二阶可导条件，仅要求折现函数一阶可导,从而避免了B样条函数在计算样条插值时的高波动性问题。L1样条定义最小化债券定价误差和折现函数的统一程式为式(5)：

(5)

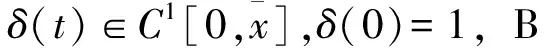
(6)

(7)

(8)

(9)

(10)

(11)

(12)

三 实验研究

1．样本选取

研究样本为上海证券交易所上市交易的20只国债每个交易日价格的历史行情数据，每条历史行情数据记录国债的代码、日期、交易价格和收益率。由于2001年之前，市场缺乏期限超过10年的长期债券，而且债券的交易品种很少，而2006年以后央行频繁调整利率水平，为了控制拟合估计偏误程度，回归分析和优化算法的样本选取期间为2002年1月4日至2005年12月29日止的920个观测日。由于2002年3月25日以后，国债交易价格是以扣除累计利息的净价法表示，因此必须加上这些债券的累计利息，得出真实的息票债券价格，全部数据来自上海证券交易所的历史行情数据库。

2．模型设定与估计

笔者通过改变样本内节点的分布模式进行敏感性分析，寻求最小化标准定价误差的节点分布。运用B样条函数估计利率期限结构的第一步是识别子区间个数和节点数目。为了获得平滑的远期利率曲线，需要使用三阶B样条函数来近似贴现函数，通过比较平均标准误差和显著系数的个数来选取适当的子区间数目，样本内的节点通过债券样本数量的均等分来确定。当子区间为4时，样本内节点设定为0, 6, 10, 15, 20的样条函数组合的7个系数在0.05水平上都是显著；当子区间个数增加时，尽管平均标准定价误差略有减少，但是估计系数的显著水平并没有显著增加；上述节点设置的平均标准定价误差是0.5326，使用不同的样本外节点，定价误差并没有显著的变化。

Vasicek和Fong指出由于无风险债券越接近于到期日时的价格越接近于债券面值，而越是远离到期日的价格波动会越大，因而无约束贴现拟合模型、约束贴现拟合模型和即期利率拟合模型的误差项不是同方差的，但是Bing和huei发现上述三个模型的误差项设定为同方差或异方差几乎不改善模型的拟合效率。因而，本文设定这些误差项具有同方差属性来进行相应的回归分析。

使用2003年6月24日的国债交易价格进行估计，表1给出不含息票因子的二项式样条拟合模型估计结果。无约束贴现函数拟合模型，有约束贴现函数拟合模型和即期利率拟合模型的所有参数估计在95%的水平上都是显著的，表明三种拟合方法的有效性；三种拟合方法的标准定价误差相近，基本上在0.6至0.7之间，其中无约束贴现拟合法的标准定价误差最大，约束贴现拟合法的标准定价误差较小，即期利率拟合法最低，但是拟合出来的利率期限结构的运动路径差异较大。

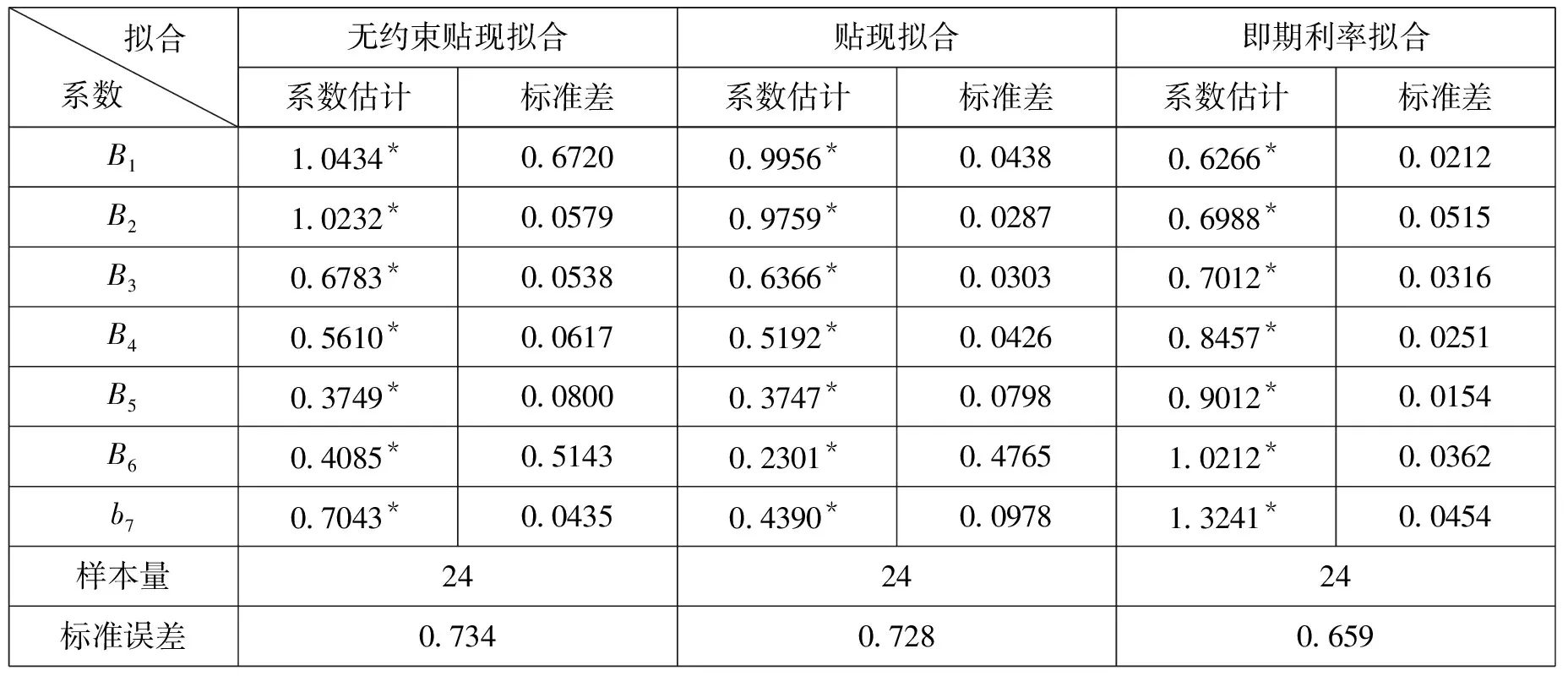
表1 不含息票因子的模型估计结果( 2003/6/24 )

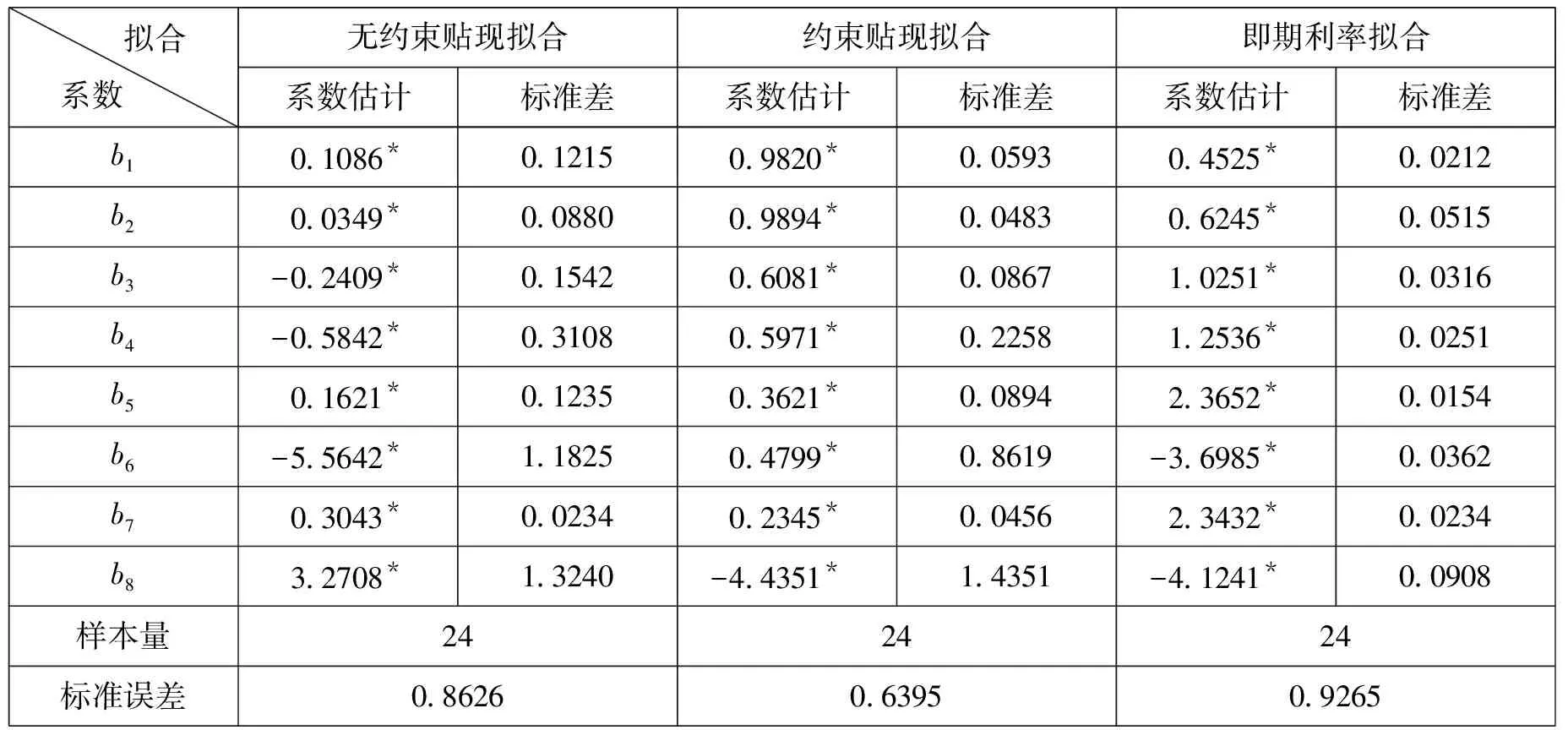
表2 含息票因子的模型估计结果(2003/6/24)

通过B样条函数估计定价模型的贴现函数与回归系数如表1所示，再运用无约束贴现拟合、约束贴现拟合和即期利率拟合即可获取整个样本期内的利率期限结构。在三种拟合方法中，无约束贴现拟合不能获得可靠和稳定的短期利率，约束贴现拟合法的标准定价误差偏大(平均达0.62)，但是能够显著地改进了短期利率估计的可靠性；在不考虑即期利率拟合法计算上的复杂性，其定价精确度略微优于约束折扣拟合法。引入付息效应和年利率水平后，标准定价误差并没有显著下降，如表2所示。通过样本区间内节点的最优化选择，拟合的精确度有了进一步的提高，即期利率拟合法的定价精确度优于约束贴现拟合法，印证了Vasicek和Fong关于利率曲线的较优拟合函数是指数函数而非二项式的观点。

从图1可以看出，无约束贴现拟合法得出的0.5年期短期利率出现了负值，这与现实不相符合；约束贴现拟合法比无约束贴现拟合法呈现更合理的利率期限结构模式，中期利率曲线呈先上升后走低，而长期利率曲线呈缓慢的上升趋势；即期利率拟合法与约束贴现拟合法(节点T5=6,T6=10和T7=15)所得的利率曲线基本上一致；约束贴现拟合法中节点T5=5,T6=8,T7=15的拟合与节点T5=7,T6=10,T7=15的拟合的曲线相似，随着期限的增加呈单调平缓上升趋势。

从图2可以看出，节点T5=6,T6=10和T7=15的B样条函数拟合的结果最接近真实的债券价格，而无约束的B样条函数拟合，节点T5=5,T6=8和T7=15的B样条函数拟合和节点T5=7,T6=10和T7=15的B样条函数拟合的结果均明显高出真实的债券价格，进一步比较图3给出的不同节点定位B样条估计定价误差三维分布，可见，B样本内有相同节点数目而不同节点的定位选择估计系数定价误差有着重大影响。

图1 不同节点组合下的利率期限结构拟合 图2 不同节点数目估计的债券价格结果比较

3．模型改进——付息效应与节点优化

上海证券交易所上市交易的国债市场收益(2002.9.23-2004.6.24)数据表明，大部分的年付息国债的市场收益率比半年付息国债来得低，这主要是由于半年付息国债都是长期国债,在市场收益率中包含流动性溢价，但是这部分国债的定价模型中却不存在付息效应，笔者在上述三种B样条拟合模型中增加付息次数因子和年付息水平因子，表2给出的回归结果b8表明付息次数和年付息因子的估计系数均不显著，这可能是因为半年付息国债的个数偏少(仅占样本国债数量的12%)有关。

图3 不同节点定位B样条估计的定价误差 图4 不同节点数目和估计方法的贴现函数

本文考虑10个节点(-3,-2,-1,0,8,15,20,25,30,35)和15个节点(-3,-2,-1,0,4,7,10,12,15,18,20,22,25,30,35)两种基本的节点组合，对于立体样条函数而言，10个节点与15个节点对应的B样条函数个数分别为6条和11条，分别拟合国债10308在期间2003.10.8-2004.6.25内的价格曲线如图5(d)所示。图5(d)显示15个节点组合拟合的定价误差明显小于10个节点，而图4中贴现函数曲线却表明15个节点组合的折现曲线波动幅度相比10个节点组合的较大，但更符合折现函数趋向于单调减少的基本特征。

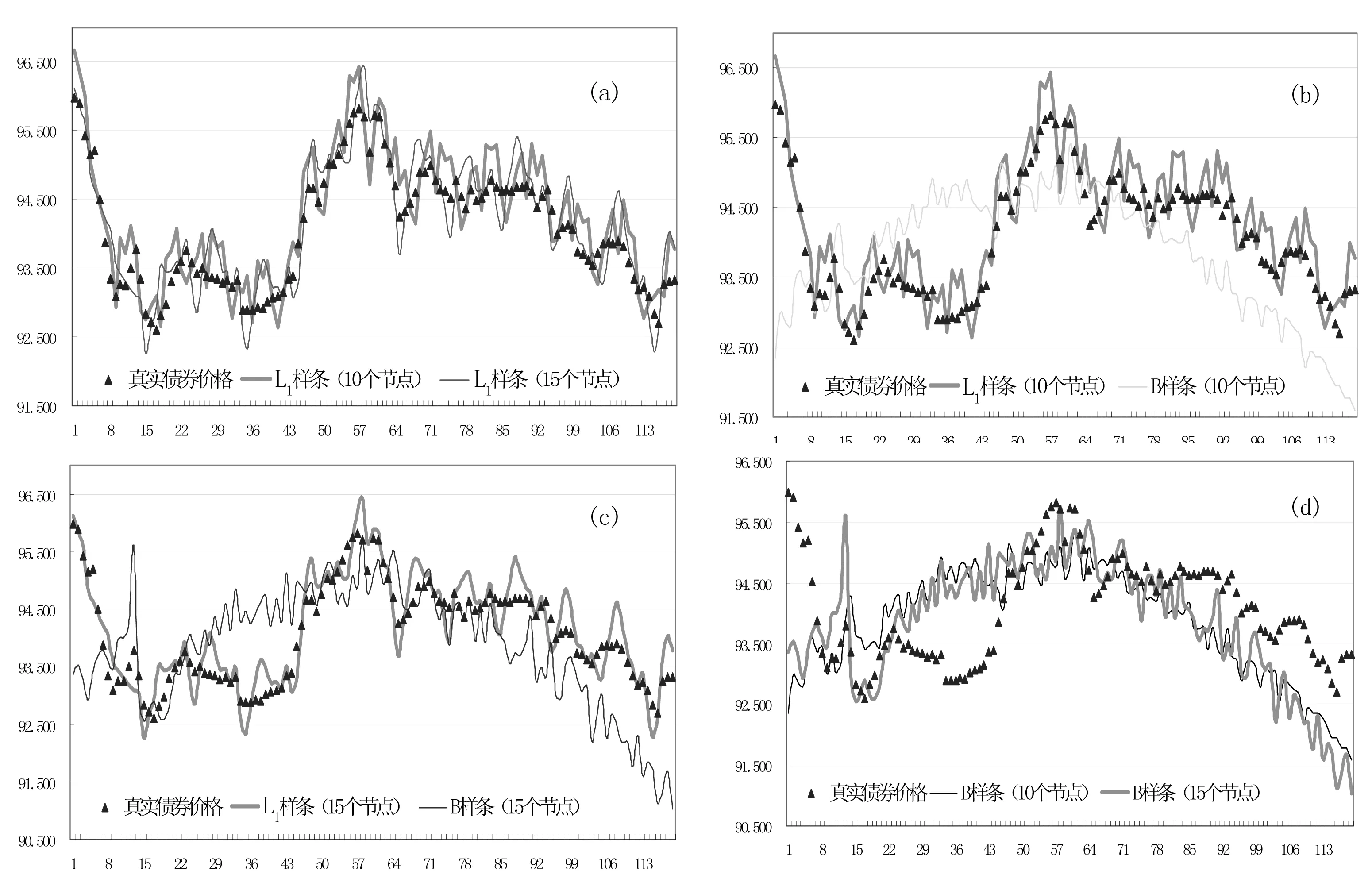
图5 不同估计技术与节点数量的拟合误差对比

具有相同节点数目而节点位置不同的组合对于拟合定价误差的影响，笔者考察了上述10个节点中的T5，T6和T7在样本期内的各种可能组合，运用约束贴现拟合模型分别求出国债10308在2003年6月24日相应的标准定价误差如图3所示，通过选取最小化的标准定价误差所对应的节点组合(T5=6,T6=10和T7=15)即为最优的样本内节点组合。笔者还将T5，T6和T7引入约束贴现拟合模型进行非线性估计，得出更精确的样本内节点的组合。值得注意的是，上述各种样本内节点组合下的模型系数估计结果都是显著的，进一步显示贴现约束B样条函数估计在稳定性和可靠性上提升。

4．L1样条估计

虽然B样条函数模型经过上述改进能够显著地提高定价精确性和减少贴现函数波动程度，但是过多人为干预和定价精确度的进一步提高仍是急待解决的问题。为此进一步引入L1样条拟合国债10308(面值100元，到期日2013年9月17日，票面利率3.02%)在期间2003.10.8-2004.6.25内的价格曲线，运用TOMLAB算法优化程序模块解决。首先编写Matlab命令文件定义债券定价公式，通过雅克比(Jacobian)矩阵实现定价可微方程与真实债券价格的最优线性逼近，将约束非线性绝对值求和最小化问题转化为约束线性最小化问题，然后运用离散非线性优化算法SNOPT(Sparse Nonlinear Optimizer)调用广义拉格朗日函数的二阶导数的准牛顿近似作为优化算法的路径，使用迭代法逐步逼近问题的可行域或最优解。

为了揭示三次多项式函数的个数对L1样条函数拟合的影响，笔者通过比较相同三次多项式个数的B样条函数，图5(b)表明具有相同节点数量与组合(-3,-2,-1,0,8,15,20,25,30,35)的L1样条的拟合误差比B样条显著变小，B样条拟合倾向刻画国债价格的长期变化趋势，而L1样条则更强调国债价格短期变动特征的捕捉，L1样条的贴现函数的波动性则明显比B样条更频繁，但L1样条拟合的贴现函数的波动频率增加的程度明显低于B样条函数。进一步提高样条节点数目，图5(a,c)表明L1样条和B样条在15个节点下的拟合精确度比在10个节点的情形均有提高，表3数据说明在运用相同数目节点拟合债券价格数据时，L1样条比B样条的拟合误差明显降低，而图4贴现函数曲线显示L1样条与B样条节点数目的提高会导致贴现函数波动性变化频率增大，这与贴现函数的单调递减性特征相背离，同时L1的拟合随着节点数目的增加对国债价格近期变动的曲线描绘更细致和精确，但L1样条在特定节点数目下比B样条的拟合耗时更长，而且随着节点数目和拟合数据量的增大明显增长(如表3)。再进一步比较B样条与L1样条的贴现函数曲线的波动特征，L1样条拟合的贴现函数曲线的变化范围在0.1-0.3之间(均值为0.2)，处于合理的波动期间，而B样条拟合的贴现函数却更多地受到人为节点数目与组合的干扰。

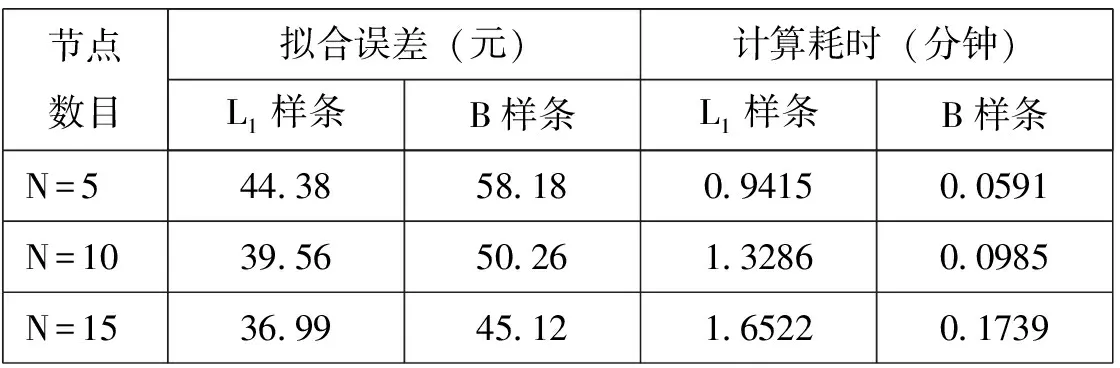
表3 L1样条与B样条的拟合误差与计算耗时

四 基本结论

本文针对国内文献对利率期限结构静态估计方法研究主要集中于息票剥离法、多项式样条函数估计、指数样条函数估计和B样条函数估计，且相应的估计定价误差较大和贴现函数的精确度较低的问题，对B样条函数进行节点优化组合和付息效应因子的模型改进，比较无约束贴现回归、约束贴现回归和即期利率回归，借助标准定价误差进行样本内节点的敏感性分析，通过估计误差最小化搜索程序和样本内节点的最优组合，获取最优的B样条函数的样本内节点分布结构，进一步降低样本数据的估计误差，拟合结果显示改进后的B样条能够增强对利率期限结构的估计可靠性, 降低除节点选择外的因素干扰。

B样条函数经过节点数目和定位的人工筛选后能够进一步降低拟合误差，而提供的贴现函数的波动程度会随着节点数目的增加而有所增大。L1样条通过最优化技术有效地提高拟合精确度，但其贴现函数的波动性相比B样条函数而言随着节点数目的增加而缓慢增大，运用自适应算法可以进一步改进L1样条节点的准确定位和改善定价的机制，同时L1样条只要求贴现函数一阶平滑条件，放宽了B样条函数对贴现函数的二阶平滑要求，从而更符合债券价格数据序列本身具有的不平滑性特征，因而较大程度提高了近似能力和解决了贴现函数的波动性问题。

国际上各种前沿的利率期限结构静态估计模型，从指数样条函数、致密样条函数、B样条函数到Chebyshev函数等，一步步地降低利率期限结构静态估计技术存在的误差，但是最为快捷、有效而准确的静态估计方法与理论的统一标准仍待进一步深入的研究和探讨。尽管本文借助B样条函数估计优化模型和L1样条估计技术，进一步改善了中国利率期限结构静态估计方法的精确度，但最优拟合函数形式和曲线平滑度问题并未得到完全解决，有关报价误差、买卖差价、税收效应和流动性差异等因素对利率期限结构估测方法的影响有待深入分析[10]99-105。

参考文献：

[1] Nelson C R, Siegel A F. Parsimonious modeling of yield curves[J]. Journal of Business, 1987, 60(4).

[2] McCulloch J H. Measuring the term structure of interest rate[J]. Journal of Business, 1971, 44(1).

[3] Steeley J. Estimating the glit-edged term structure: basis splines and confidence intervals[J]. Journal of Business Finance & Accounting, 1991,18 (4).

[4] Coleman, Thomas S, Fisher, Lawrence, Ibbotson, Roger G. Estimating the term structure of interest rates from data that include the prices of coupon bonds[J]. Journal of Fixed Income, 1992, 2(2).

[5] Chambers, Donald R, Carleton, Willard T Waldman, Donald W. A New Approach to Estimation of the Term Structure of Interest Rates[J]. Journal of Financial & Quantitative Analysis, 1984, 19(3).

[6] Vasicek, Oldrich A, Fong H Gifford. Term structure modeling using exponential splines[J]. Journal of Finance, 1982, 37(2).

[7] 郑振龙，林 海. 中国市场利率期限结构的静态估计[J]. 武汉金融, 2003, 39(3).

[8] 傅曼丽，董荣杰，屠梅曾. B-样条法构建利率期限结构的实证研究[J]. 哈尔滨工业大学学报：哲学社会科学版，2007, 39(8).

[9] Cheng H, Fang S C, Lavery J E. Univariate cubic L1splines-a geometric programming approach, Mathematical Methods of Operations Research[J]. 2002, 56(2).

[10] 吴泽福. 利率期限结构波动效应的协整实证[J]. 华侨大学学报：自然科学版, 2010, 31(1).