非对称效应视角下的中国通货膨胀不确定性实证研究

○苏梽芳

(华侨大学 经济与金融学院，福建 泉州 362021)

一 引 言

货币经济学中的一个重要问题是研究更高的通货膨胀是否会导致更高的通货膨胀不确定性(Friedman-Ball假说)。研究者一般认为，如果对此问题的回答是肯定的，那么，人们对通货膨胀具有社会成本的观点将持更加肯定的态度，而且也将更深刻地认识到这种成本的来源与本质：通货膨胀之所以具有社会危害性，是因为当经济社会发生通货膨胀时，公众通货膨胀预期不确定性的增加，降低了市场价格作为协调经济活动机制的效率，造成了整个经济系统信号的紊乱，从而降低了资源配置的效率，同时也造成了经济的波动。因此研究通货膨胀与通货膨胀不确定性之间的关系具有重要的理论意义与现实意义。

从已有的国内外相关文献来看，Friedman-Ball假说得到了大多数文献的支持，然而仍存在的一个分歧是：通货膨胀正负冲击对通货膨胀波动性作用的非对称性是否存在，即同等程度的通货膨胀或者通货紧缩冲击是否导致同等程度的通货膨胀不确定性。对此，目前的国内外研究文献尚未给出比较明确和统一的推断。相比国外较为丰富的研究，目前，国内学者对中国通货膨胀不确定性研究文献较少，而研究通货膨胀冲击非对称效应的文献则更少,在为数极少的文献当中，如赵留彦等[1]60-72，胡日东等[2]29-38，许志宏[3]，Menelaos et al.[4]265-286，还存在如下的不足之处：第一，研究文献往往只采用单一模型进行非对称性检验，缺乏基于不同检验方法的结论的相互印证，致使实证结论的可靠性难以保证；第二，更为重要的是，目前国内相关研究文献均未能把通货膨胀不确定性区分为长期成分与短期成分，并从中分离出长期成分，而这可能会影响通货膨胀冲击非对称性效应检验的结论。对于第一点不足，需要采用更长样本区间的数据和多种形式的条件方差模型来检验通货膨胀冲击的非对称性作用，以便增强所获得的经验结论的稳健性。对于第二点不足，国外的一些文献所采用的方法值得借鉴。如Ball和Cecchetti[5]215-254应用一个简单的不可观测成分模型把美国通货膨胀率分解为持久成分与短暂成分，他们发现，相对于暂时冲击方差，持久冲击方差与通货膨胀水平存在更大的相关关系，由此得出更高的通货膨胀水平将导致更大的长期通货膨胀不确定性的结论。而Kim[6]341-349的研究在应用计量模型方面上更进一步，他把普通的不可观测成分模型扩展为具有马尔可夫机制转换的不可观测成分模型，发现了类似的结论。Kontonikas[7]525-543则应用成分GARCH模型以检验英国采用通货膨胀目标制后是否显著地降低了通货膨胀持续性与长期通货膨胀不确定性。Kevin和Ye[8]应用非对称的随机波动模型对美国的数据展开实证检验，贝叶斯MCMC的估计结果显示，无论是长期还是短期，更高的通货膨胀都不会导致更高的通货膨胀波动。

在借鉴上述研究文献的基础上，本文应用非线性GARCH模型族侧重研究通货膨胀不确定性对通货膨胀冲击的非对称反应。在检验存在通货膨胀冲击非对称性基础上，进一步应用非对称成分ARCH模型把通货膨胀不确定性分解为长期成分和短期成分，在长期成分方程中引入一个虚拟变量，从而对1996年中央银行宣布以货币供应量作为货币政策中介目标以来通货膨胀不确定性长期成分是否明显降低进行检验。本文对国内已有研究通货膨胀不确定性相关文献构成两点贡献。第一，本文应用多种非对称GARCH模型验证了中国通货膨胀冲击的非对称效应的存在，各种非对称模型研究结果互相支持、佐证，增强了结论的稳健性。尤其是本文应用非对称成分ARCH模型，克服了以往国内研究没有区分通货膨胀不确定性长期成分与短期成分的缺陷；而基于不同非对称GARCH模型信息冲击曲线的绘制更加直观地呈现出通货膨胀冲击的非对称性特点。第二，本文在非对称成分ARCH模型引入了虚拟变量，验证1996年中央银行实行以货币供应量为中介目标的制度设计是否显著地降低了通货膨胀不确定性的长期成分，而之前国内相关文献未从降低通货膨胀不确定性长期成分的角度对以货币供应量为中介目标的制度的作用做出评价。

全文组织如下:第二部分应用多种非对称GARCH模型与信息冲击曲线检验与描述通货膨胀冲击非对称性；第三部分，进一步在非对称成分ARCH模型框架内检验货币供应量中介目标引入后是否显著地降低了通货膨胀不确定性的长期成分；最后一部分为结论与政策启示。

二 通货膨胀冲击的非对称特征

(一)平稳性检验与ARCH效应检验

本文使用的是同比通货膨胀率月度数据，数据来源于中国经济信息网数据库，样本区间为1983.1-2009.2，共314个样本点。

在对模型进行估计之前,我们先对通货膨胀率序列进行单位根检验。结果发现,无论是ADF或者是PP检验,在10%的显著性水平下,均拒绝单位根假设。其中，ADF检验结果显示，在由AIC准则确定的、最优滞后阶数为15且不包含时间趋势但包含截距项的条件下，ADF统计量为-2.607,小于10%的临界值为-2.571,它犯第一类错误的最大概率是0.092，概率较小，因此在10%水平下拒绝通货膨胀过程存在单位根的零假设。PP单位根检验则显示，在只包含截距、最优滞后阶数为2项的条件下，PP检验统计值为-2.754,10%的临界值为-2.571,同样在10%水平下拒绝通货膨胀过程存在一个单位根的零假设。

国内外经验研究结果普遍认为，自回归模型可以较好地拟合通货膨胀的动态过程。对于自回归模型的滞后阶数，本文通过AIC准则进行选择，设定最大滞后阶数为12，逐次进行回归，最终回归模型估计结果为：

πt=1.508πt-1-0.517πt-2

t=(30.603) (-10.493)

这个回归方程的估计系数十分显著，而且拟合的程度也很好(R2=0.985)。对该自回归模型的残差进行ARCH-LM检验，得到了在滞后阶数5时的ARCH-LM检验结果。检验结果显示,检验统计量的伴随概率P值为0.0047，小于显著性水平0.05，因此拒绝“残差中不存在条件异方差”的零假设，说明通货膨胀率自回归模型估计后的残差中不仅存在条件异方差，而且是较为高阶ARCH效应,即存在GARCH效应。

(二)非对称GARCH模型族的估计结果

TGARCH模型、EGARCH模型以及PARCH模型是三种非常重要的非对称GARCH模型，应用这三种模型对通货膨胀率进行建模，可以检验通货膨胀冲击是否存在非对称效应。

这部分给出分别应用对称的GARCH模型、GARCH-M模型、TGARCH模型、EGARCH模型以及PARCH模型对通货膨胀率时间序列进行拟合的结果，结果见表1。

表1 非对称GARCH模型族的估计结果

首先应用AR(2)-GARCH(1，1)模型对通货膨胀时间序列进行拟合，结果见表1的第二列。而后对模型的残差进行ARCH-LM检验，得到了滞后阶数为8时的ARCH-LM检验统计量的P值为0.753，因此不能拒绝“残差中不存在条件异方差”的零假设，表明GARCH(1,1)模型的残差中不存在条件异方差。于是我们可以使用GARCH(1,1)模型残差的条件方差或者条件标准差度量通货膨胀不确定性。

图1给出了通货膨胀不确定性的动态路径。1983.1-2009.2期间，通货膨胀不确定性出现了四次峰值。第一次出现在1985-1986年期间，预期不确定性表现为突然性高涨，随即便回落到较低水平；第二次是1988-1989年之间，预期不确定性逐渐增大并在1988年底达到峰值；第三次是1993-1994年之间，不确定性再一次达到较大的峰值；第四次是在2004年，公众通货膨胀预期高度不确定，预期值的离散程度较大，且这种现象持续了一段时间。

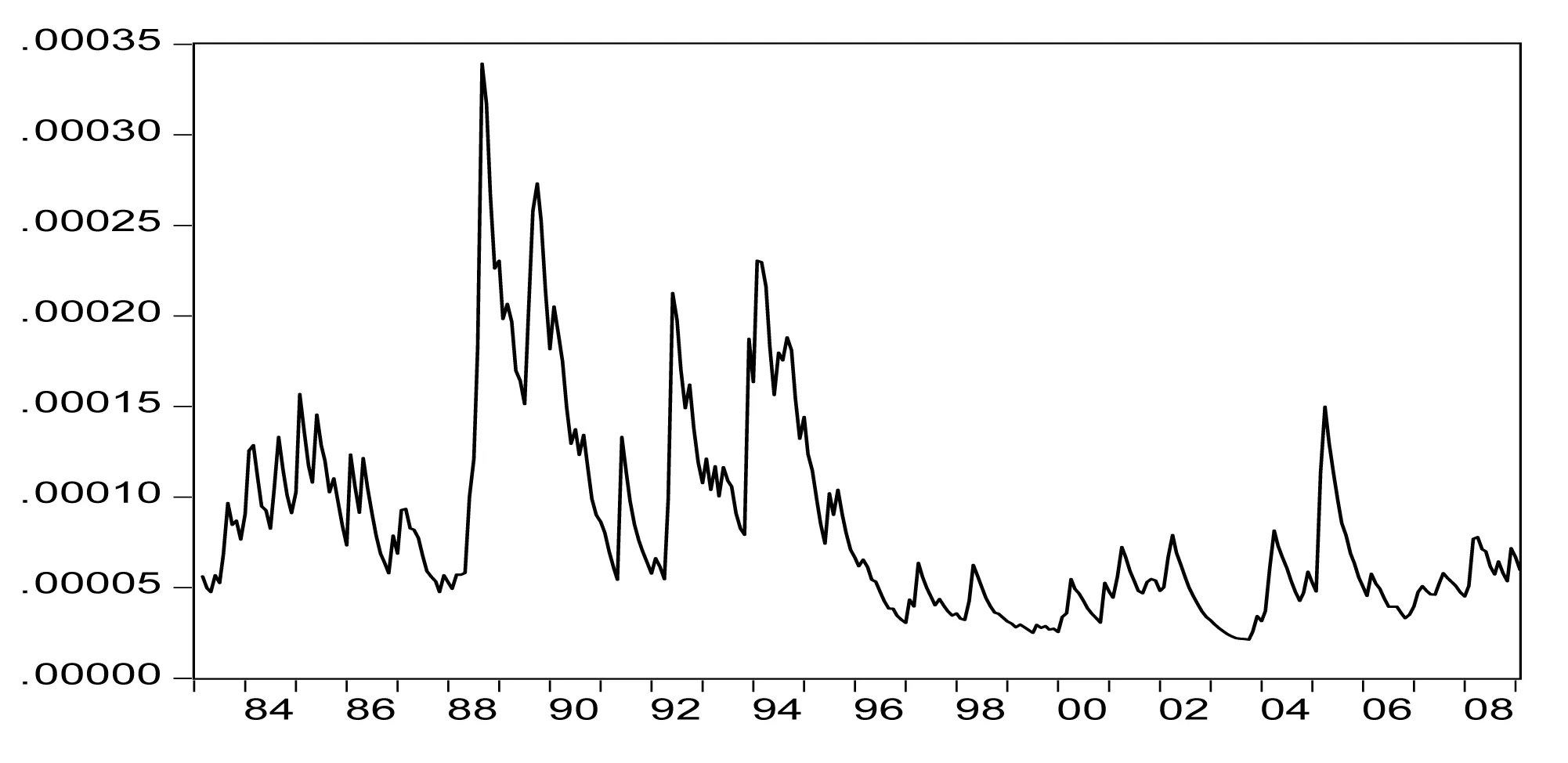
图1 通货膨胀不确定性时间路径(1983.1-2009.02)

在对称GARCH模型的条件方差方程中加入通货膨胀率的滞后一期，得到AR(2)-GARCH(1,1) -M(1)模型，用以检验是否较高的通货膨胀伴随着较高的通货膨胀不确定性(结果见表1的第三列)。从GARCH-M模型的估计结果看，条件方差方程中系数φ的估计值在1%水平下显著为正，这意味着，更高的通货膨胀水平将导致更高的通货膨胀不确定性，支持了Friedman-Ball假说。

以上的检验结果表明较高的通货膨胀率引起较强的通货膨胀不确定性，但上述模型中条件方差对于外部正负冲击的变化是对称的，而实际上存在一些经济变量对同样程度的正负冲击表现出不一致的反应。比如，较高的通货紧缩率也将引起较强的不确定性，那么相同强度的通货膨胀冲击与通货紧缩冲击对通货膨胀不确定性的影响程度是否相同？对此我们采用了由Glosten et al.[9]1779-1801首先提出的非对称门限GARCH(TGARCH)模型，该模型是比较通货膨胀冲击与通货紧缩冲击对通货膨胀不确定性影响的有效工具。

根据TGARCH模型，“坏消息”(εt<0)与“好消息”(εt>0)对条件方差有不同的影响，其中“坏消息”的影响为α+γ，“好消息”的影响是α。对于通货膨胀率的TGARCH模型来说，“坏消息”意味着通货紧缩冲击，“好消息”意味着通货膨胀冲击。如果γ显著小于零，则α+γ<α，说明通货紧缩冲击引起的不确定性小于通货膨胀冲击引起的不确定性；如果γ显著大于零，则α+γ>α，说明通货紧缩冲击引起的不确定性大于通货膨胀冲击引起的不确定性；如果γ等于零，则α+γ=α，说明通货紧缩冲击引起的不确定性等于通货膨胀冲击引起的不确定性。

TGARCH模型估计结果参见表1中的第四列。对模型估计后的残差进行ARCH-LM检验，得到了滞后阶数为6时的ARCH-LM检验统计量在5%水平下显著，因此不能拒绝“残差中不存在条件异方差”的零假设，表明TGARCH(1,1)模型的残差中已经不存在条件异方差。TGARCH(1,1)模型估计结果显示，参数γ=-0.203在1%水平下显著小于零，因此可以得出结论：通货紧缩冲击引起的不确定性小于通货膨胀冲击引起的不确定性。

在EGARCH模型估计结果中，系数α的估计值为0.115，非对称项r的估计值为0.103。当εt-1>0时，该信息冲击对条件方差的对数有一个0.115+0.103=0.218倍的冲击；当εt-1<0时，它给条件方差的对数带来的冲击大小为0.115×(-0.103)=0.012倍。在TGARCH模型中，通货紧缩冲击引起的不确定性小于通货膨胀冲击引起的不确定性的结论在EGARCH模型中得到了进一步的印证。而Ding、Granger和Engle[10]83-106对标准GARCH模型的进一步拓展提出的PARCH模型同样可以检验冲击的非对称效应，在该模型估计结果中(表1的第6列)，我们发现用于捕捉非对称效应的参数γ=0.929在1%水平下显著不为零，进一步证实了相同强度的通货膨胀冲击与通货紧缩冲击对不确定性的影响程度是不相同的。

(三)非对称GARCH模型的信息冲击曲线

信息冲击曲线是由Engle和Ng[11]1749-1778所提出的,该曲线的绘制可以使得信息冲击的非对称影响表示得更加直观。以EGARCH(1,1)模型为例,将EGARCH(1,1)模型的条件方差方程改写为如下形式:

(1)

记f(ut-1/σt-1)=α|ut-1/σt-1|+γ(ut-1/σt-1)

(2)

上式简化为：f(Zt)=α|zt|+γzt-1zt=ut+σt

(3)

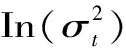
图2与图3分别是根据表1中EGARCH(1,1)模型与TGARCH(1,1)模型估计结果所绘制的信息冲击曲线。从图2、3中我们可以看到信息冲击对预期不确定性造成的非对称影响：这条曲线在信息冲击小于0时，也就是出现负向冲击时，比较平缓，而在正冲击时则比较陡峭。这就说明了通货膨胀正冲击使得通货膨胀不确定性的变化更大一些。这一结论与胡日东等[2]、苏梽芳等[12]39-44应用随机场回归模型与分位数回归模型所得到的结论相类似。

图2 EGARCH模型的信息冲击曲线 图3 TGARCH模型的信息冲击曲线

三 检验货币供应量为中介目标是否降低通货膨胀不确定性长期成分

在较长时间内，我国货币政策的中介目标和操作目标的划分界限一直含糊不清。一开始是把现金和贷款规模作为货币政策中介目标的操作目标。然而，随着金融市场的不断发展和金融资产的多元化，现金计划与信贷计划逐步变得“不可计划”和“不可控制”，中央银行很难实现预定信贷计划目标。“现金计划”和“信贷规模”与通货膨胀率以及实际经济增长目标之间的相关性也被削弱，通过信贷计划来实现物价稳定已经不适宜。1996年,货币供应量被正式确定为我国货币政策中介目标。虽然作为中介目标的货币供应量在可测性、可控性方面存在严重缺陷,并且从实践情况来看,货币供应量的实际值与目标值之间存在很大的离差,在稳定价格并以此促进经济增长方面也不能令人满意。但是1998年后，各经济变量波动较为平缓，反映出我国货币政策调控方式更注意宏观调控的前瞻性、科学性，注重调控的“时”与“度”，较好地把握了“预调”、“微调”，使宏观经济较为平稳增长,价格水平同时也保持较为平稳的走势。

通货膨胀动态过程在1996年前后呈现出不一致的特点，是否与中央银行实行货币供应量为中介目标的货币政策有关？为检验这个假设，我们首先设计了非对称的成分ARCH模型进行非对称效应的检验，继而在长期波动成分方程中加入虚拟变量dummy以检验1996年中央银行实行货币供应量为货币政策中介目标后是否显著地降低了通货膨胀不确定性的长期成分。虚拟变量dummy的具体取值设置为：1996年之前，dummy取值为0，1996年之后取值为1。模型设计如下：

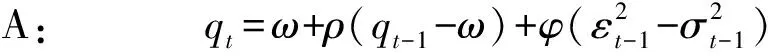
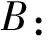
模型A为非对称成分ARCH模型，模型B为在长期成分方程中引入虚拟变量dummy的非对称成分ARCH模型。其中，ω是无条件方差，模型中的第一个方程与第二个方程分别是长期成分方程与短期成分方程。在成分ARCH模型的条件方差方程中，可以包含外生变量。这个外生变量可以放在长期成分方程中，也可以出现在短期成分方程中。短期成分方程中的外生变量将对变化率的短期移动产生影响，而长期成分方程中的变量将影响变动率的长期水平。两个模型最终估计结果见表2。

表2 非对称成分ARCH模型估计结果

由上面模型A、B的估计结果可知,模型A中的非对称项的系数λ=-0.333在1%水平下显著不为零，因此支持了通货膨胀冲击非对称性效应的结论。模型B中的非对称项的系数λ=-0.195在1%水平下显著,支持了模型A的实证结论。由于虚拟变量dt表示负的冲击,所以这种效应就可以解释为正的冲击效应要比负的冲击效应大。但是,这种非对称效应只出现在短期成分方程中，可以说出现这种非对称效应只是暂时的。而它对长期波动率qt的影响是：它使长期方程中的ρ减小为0.270,这将导致长期波动率qt以较快的速度收敛于稳定的状态值。

虚拟变量dummy的估计系数为η=-0.0001在1%水平下显著，这表明1996年中央银行以货币供应量作为货币政策中介目标一定程度上降低了通货膨胀不确定性的长期成分。究其原因，1996年以前正是我国货币政策及其调控机制和宏观经济发生相对剧烈频繁变化时期，这种激烈的变化同时也导致公众通货膨胀预期更加不稳定，通货膨胀预期处于高不确定性状态。1996年以来，中央银行逐步建立起以基础货币为操作目标、货币供应量为中介目标的货币政策调控机制，货币政策总体上也保持一种相对稳健态势，且宏观经济的内在稳定性得到明显增强，公众的通货膨胀预期不确定性的长期成分相对于过去已大为降低。图4给出的通货膨胀不确定性长期成分的自1996年以来表现出持续下降变化的趋势支持了上述的论述。

图4 通货膨胀不确定性(浅黑线)与通货膨胀不确定性长期成分(深黑线)

四 主要结论

本文基于中国1983.01-2009.02期间的月度CPI数据，运用多种非对称的GARCH模型，对通货膨胀冲击的非对称特征以及1996年货币供应量为货币政策中介目标的引入是否显著降低了通货膨胀不确定性长期成分展开实证研究，由此产生的结论与政策含义有：

第一，实证分析的结论支持Friedman-Ball假说成立，这个结论意味着通货膨胀成本很大程度上和通货膨胀不确定性的成本联系在一起，因此稳定价格和维持低通货膨胀环境可能成为中央银行减少通货膨胀不确定性、继而降低通货膨胀所带来社会危害的重要手段。

第二，各类非对称GARCH模型的实证结果与信息冲击曲线显示，相等程度的通货膨胀冲击与通货紧缩冲击对通货膨胀不确定的影响程度并不相同:通货膨胀冲击引发的通货膨胀不确定性高于由于通货紧缩冲击引发的通货膨胀不确定性。这个结论无疑具有重要的政策含义，即中央银行在经济处于通货膨胀时期应比面对通货紧缩时期应更加注重引导公众的预期，更加重视预期管理。

第三，虽然从可测性、可控性与国民经济的相关性以及抗干扰性等几个标准来看，1996年开始实行的以货币供应量作为货币政策中介目标的政策设计都受到了不断的质疑，但客观上一定程度降低了通货膨胀不确定性的长期成分。这个结论对于我国中央银行将来进行货币政策操作框架的设计，比如考虑引进当前国际流行的通货膨胀目标制具有重要的政策启示。

参考文献：

[1] 赵留彦,等.中国通胀水平与通胀不确定性：马尔柯夫域变分析[J].经济研究，2005,(8).

[2] 胡日东,苏梽芳.中国通货膨胀与通货膨胀不确定性的非线性关系[J].数量经济技术经济研究,2008,(2).

[3] 许志宏.中国通货膨胀的动态特征与预测研究[D].长春：吉林大学商学院，2008.

[4] Menelaos K,Stefanie S.Is the Relationship between Inflation and Its Uncertainty Linear?[J].German Economic Review,2008,(3).

[5] Ball L,Cecchetti S.Inflation and Uncertainty at Long and Short Horizons[J].Brookings Papers on Economic Activity,1990,(21).

[6] Kim C J.Unobserved Component Time Series Models with Markov-Switching Heteroskedasticity:Changes in Regime and the Link between Inflation Rates and Inflation Uncertainty[J].Journal of Business and Economic Statistics,1993, (75).

[7] Kontonikas A.Inflation and Inflation Uncertainty in the United Kingdom:Evidence from GARCH Modelling[J].Economic Modelling,2004,(21).

[8] Kevin G,Ye H.Does High Inflation Predict Greater Inflation Uncertainty?:Evidence from Asymmetric Stochastic Volatility Models[Z].Working paper, April 2007.

[9] Glosten L,Jaganathan R,Runkle D.On the Relation between the Expected Value and the Volatility of the Normal Excess Return on Stocks[J].Journal of Finance,1993,(48).

[10] Ding Z, Granger C W J,Engle R F.A long Memory Property of Stock Market Returns and a New Model[J].Journal of Empirical Finance,1993,(1).

[11] Engle R F,Victor K Ng .Measuring and testing the impact of news on volatility[J].Journal of Finance,1993,(48).

[12] 苏梽芳,胡日东.中国通货膨胀水平与通货膨胀不确定关系：分位数回归[J].宏观经济研究,2009,(5).