基于分块小波微粒群混合的图像智能检索
罗涛华,沈显君
(1.武汉工业学院 计算机与信息工程系,湖北 武汉 430023;2.华中师范大学 计算机科学系,湖北 武汉 430079)
近年来,包括图像在内的各种多媒体数据的数量正以惊人的速度增长,如何提供一个有效的算法来快速、准确地查询这些具有丰富内涵的图像信息成为当今检索领域的研究热点和难点之一.基于内容的图像检索CBIR(content based image retrieval)技术已成为解决这一问题的关键技术之一.该技术往往通过提取、比较图像的特定特征而完成检索.这些特征主要通过图像像素的颜色分布[1]、图像中物体的性质[2]、图像的纹理[3]等表现出来.由于颜色旋转、标度的不变性以及尺寸、方向的不敏感性等天然特性,使其成为图像检索系统中运用最为广泛的特征之一.本文中分析当前基于直方图的图像检索系统有限的有效性,将直方图算法与小波分块技术相结合,提出基于分块小波变换的图像检索算法.小波变换能够将图像分解成若干具有不同频率的子图像,以提取整图像的主要结构信息和细节信息,同时,图像的空间特征通过分块小波直方图法进行描述,以增强检索性能.
实验证实,分块小波图像检索算法虽然比直方图算法的检索准确率有了较大提高,但在执行速度上却明显变慢,因此,需要引入某种优化算法来加快其搜索速度.粒子群是近年来优化算法领域中强大的竞争者,它将图像检索描述为一个组合优化问题,而适应度函数则描述为图像的相似性度量函数.适应度函数结合分块图像小波变换信息和颜色子直方图中的欧氏距离来计算.据此,本文中提出一种新的检索策略:将分块小波技术和微粒群算法与一般的基于颜色直方图的图像检索算法相结合,得到基于微粒群和分块小波变换的图像检索新算法.
1 基于直方图的相似度搜索
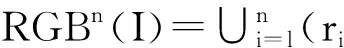
(1)
其中ri、gi、bi分别是红色、绿色和蓝色的第i个颜色值.直方图描述了样品在一组相邻间隙内的分布.为了建立直方图,图像的每个像素均被作为能够产生相对频率矢量的取样点[4].在RGBn颜色空间中,图像I的颜色直方图是矢量: H(I)=(hc1(L),hc2(L),…,hci(L),…)
(2)
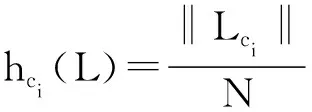
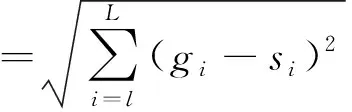
(3)
其中,Ed表示的是图像G和图像S之间的欧氏距离,Ed越小,相似度就越大;gi是图像G的颜色直方图信息;si是图像S的颜色直方图信息;L为颜色级数.
我们称上述方法为颜色直方图图像相似度检索法(ContentHistogram-BasedImageRetrieval),简称为CHIR算法.此算法的核心思想是将图像看成是一个整体,首先计算图像的直方图信息;然后通过欧氏距离公式对两幅图像的直方图信息进行差值计算,得到两幅图像间的距离,距离越小,表示两幅图像相似度越高,反之也成立;最后按照距离从小到大的顺序(也就是相似度从大到小的顺序)显示搜索结果.用CHIR算法进行多个算例的仿真实验,得出各算例的图像检索率主要在0.4~1.0之间变化.检索率是图像检索准确度的评价准则之一,其计量方法为η=nrelevant/Ngroup(nrelevant为搜索后特定组中检索出的相似图像数,Ngroup为当前组中的相似图像的总数).该算法检索率变化范围较大,因为其只考虑到整幅图像的直方图信息,而不考虑空间位置等其他信息,导致检索准确率低.
2 分块小波直方图算法
传统的颜色直方图只记录颜色信息,因其稀疏、容易受噪音影响,故检索精确度大打折扣,因此,一些直方图信息类似的图像其外观可能有天壤之别.另外,颜色直方图不包含任何空间信息,导致算法的性能较低.针对这一问题,我们将分块小波技术和直方图算法相结合,在一定程度上提高检索结果.
小波是将数据分成不同频率成分、然后使用与其标度匹配的分辨率对每个成分进行解读的数学函数.如果进行了多尺度小波变换,即可获得低频率、高频率成分.借助于这些低频率、高频率矢量,即可测得相似度,从而了解各层次的结构[5].
图像相似度测量使用的是分块小波直方图法(BlockingWavelet-HistogramImageRetrieval),简称BWHIR算法.该方法将分块小波与颜色直方图的欧氏距离相结合.具体地说就是将原始图像分割成N个小块,分别对每个子块进行小波分解,取出分解后的低频信息部分,然后对每个子块中的低频部分分别计算子直方图值,将原始图像与待比较的图像按子块进行直方图欧氏距离比较,最后计算各个子块距离的平均值,即为两幅图像之间的分块小波距离值,距离值越小表示两幅图像越相似,反之,两幅图像越不相似[6].图1是一幅图像的2×2小波分解.
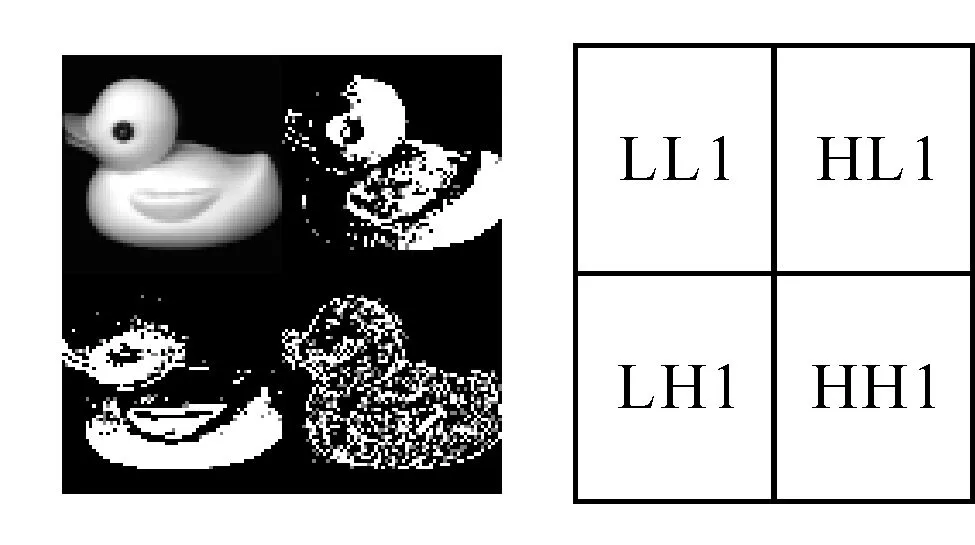
图1 2×2小波分解
在图1中,LL1是图像低频率成分,LH1、HL1和HH1是高频率成分.LH1是一般图像水平方向低通、垂直方向高通的细节信号;HL1是一般图像水平方向高通、垂直方向低通的细节信号,HH1是图像对角线方向的细节信号.Sim(G,S)是两个图像的相似度测量.
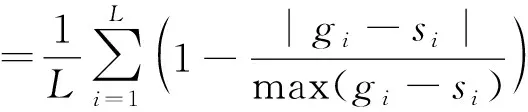
(4)
两个图像的相似度测量值取各小块相似度测量值的平均值,可以将其视为是涉及图像检索适应度的问题,并通过方程进行定义:
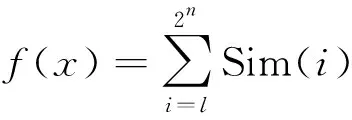
(5)
式中f(x)是是适应度函数,2n是分块图像的尺寸,Sim(i)表示第i个子块的子直方图距离.仿真实验中用BWHIR算法对CHIR算法中所有算例进行检索发现,其检索率在[0.92,1.0]之间变化,比CHIR的[0.4,1.0]变化范围明显变小,且同组算例图像的搜索效率均有较大提高.
3 分块小波变换和微粒群混合算法
尽管BWHIR算法比CHIR算法具有更优越的效率,但是它们需一个个地将查询图与候选图进行比较,因此在本质上属于枚举算法.如果图像数据库庞大,那么枚举算法的运行效率则让人无法容忍,因此需要寻找更加高效的图像检索法.研究发现结合微粒群算法能提供可行解.
3.1微粒群算法微粒群PSO(particleswarmoptimization)是一种基于群体智能理论的迭代优化算法.系统初始化为一组随机解,并由目标函数为之确定一个适应值,每个粒子根据自己和其他粒子的飞行经验在解空间中进行迭代搜索.假设在—个n维的搜索空间中,有m个粒子组成—个群体,其中第i个粒子的当前位置可以描述为Xi=(xi1,xi2,…,xin),将Xi代入一个目标函数就可以算出其适应值.第i个粒子的速度可表示为Vi=(vi1,vi2,…,vin);第i个粒子的个体最优值可表示为Pi=(pi1,pi2,…,pin);群体目前找到的最优值记为Pg=(pg1,pg2,…,pgn).每个粒子根据如下的公式来更新自己的速度和位置:
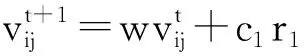
(6~7)
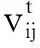
w(t)=(wini-wend)(Tmax-t)/Tmax+wend
(8)
其中T指的是当前迭代,Tmax是当前迭代的最大值,wini为初始惯性权重(一般取值0.9),wend为运行终止时的惯性权重(一般取值0.1).
从上述进化方程可以看出,在每次迭代中,粒子通过跟踪自己搜索到的最好的解和整个粒子群经历过的最好位置来不断更新自己在解空间的位置和速度,从而产生下一代群体,这种特有的记忆使其可以动态跟踪当前的搜索情况调整其搜索策略[8].因此从原理上可以把粒子群算法和图像库相似性搜索问题相结合,只需要根据进化算法,对图像库中的一部分图像实行智能的选择,代替每幅图像依次进行匹配的方法,从而适当加快算法的执行速度.
3.2分块小波与微粒群混合算法设计将检索问题的可行解概念化为在图像数据库中飞行的粒子,其行为由搜索和共享群中图像匹配信息的最佳适应度法则支配.粒子在数据库中搜索图像,并将数据库中的候选图像与搜得的图像进行比较,其过程是粒子在解空间中的移动.图像的序列号表示粒子的位置;粒子的速度描述在检索过程中搜索到的两个图像之间位置的变化.
第i个粒子之前的最佳位置是该粒子已经搜索到了最佳匹配图像序列号时的位置.最佳粒子的位置是目前为止整个粒子群在图像数据库中搜索到了最佳匹配图像的序列号时的位置.即使粒子的速度受PSO最佳法则的影响不断更新,但是其需要的是一个整数,因为粒子的位置也是整数.我们将该算法称之为基于粒子群优化与分块小波直方图图像检索法,简称为BWPSOIR算法.
该算法的核心思想是用微粒群算法对图像库的搜索策略进行优化,将微粒群算法与小波分块算法相结合,实现智能搜索的目的.首先对微粒群的初始位置和速度进行初始化,其过程为:(1)用一个字符串数组char *image[N]来存放图像库中所有图像的名称,这样就可以将图像i(i=0,1,2,…,N-1)作为微粒变量来考虑,从而设定群体规模N;(2)对任意微粒i的第j维,在[0,N-1]内服从均匀分布产生位置xij;(3)对任意i,j,在[0,Vmax],Vmax为设定的最大速度,一般取常数(3)内服从均匀分布产生速度vij.然后通过群体中微粒的相互作用和竞争产生的群体智能指导优化搜索,它特有的记忆使其可以动态跟踪当前的搜索情况调整其搜索策略,当达到结束条件(通常为足够好的适应值)或达到一个预设最大代数(Gmax),则搜索结束.
算法设计的具体步骤为:(1) 输入待搜索的原始图像的名称,计算其小波分块直方图信息;
(2) 初始随机选择n个图像为初始解Xi=(xi1,xi2,…,xin),并对其速度Vi=(vi1,vi2,…,vin)进行初始化;
(3) 根据式(4)和式(5)计算图像库中每个图像的适应值,即分别计算初始解中各幅图像与输入图像的距离;
(4) 对每个微粒(图像),将其适应值与所经历过的最好位置Pi的适应值进行比较,取优作为当前的最好位置;
(5) 对每个微粒,将其适应值与全局所经历的最好位置Pg的适应值进行比较,取优作为当前的全局最好位置;
(6) 根据(6)、(7)和(8)式对微粒的速度和位置进行进化;
(7) 如未达到结束条件(通常为足够好的适应值或一个预设最大代数),则返回步骤(3);达到则结束.
4 实验结果及分析
为了评估上述3种方法的有效性,我们借助于哥伦比亚侯选图像图书馆(COIL-12,为一开放的网上图像数据库)、MATLAB7.0.6和Microsoft Visual C++6.0模拟软件进行最佳匹配图像检索实验,同时记录每组图像的匹配检索结果和算法的运行时间,算法的性能主要用图像搜索准确率和检索时间来度量.我们将下载的20 000张图像进行分析整理形成试验用图像库,并根据图像的相似程度不同将它们分成100组,每组200张,组编号为obj1~obj100,每组中的待匹配图片按位置顺序依次编号为1~200,每个查询图像随机从试验用图像数据库中抽取,每个图像被分成尺寸为16×16的小块 .
因为算例数组太多,我们抽取3组(其中汽车、猫、小猪的样品各取200)显示检索的图像结果.图2、图4和图6是随机从第一组、第二组和第三组图像中抽取出来的3个查询图像.图3、图5和图7是通过BWPSOIR算法获得的5个最佳匹配图像(匹配度从大到小).

图2 第一组的查询图

图3 第一组的最佳匹配图像

图4 第二组的查询图

图5 第二组的最佳匹配图像

图6 第三组的查询图

图7 第三组的最佳匹配图像
通过对记录的3种算法同组最佳匹配图像检索结果分析可知,BWPSOIR算法和BWHIR算法所得到的结果图像与输入的原始图像更相似,而用CHIR算法进行最佳匹配图像检索则容易陷入直方图与输入图像相似的干扰图像中,往往得不到正确的图像结果.
表1记录了上述3种方法在图像数据库中检索相同查询图像时的检索效率和所用的检索时间.

表1 检索效率和检索时间
通过对表1中的数据结果进行比较分析可知,在进行最佳匹配图像检索时,CHIR算法速度最快、检索效率最低;BWHIR算法速度最慢,需要用多出CHIR算法几倍的时间,而检索效率几乎与BWPSOIR算法一样好;BWPSOIR算法速度介于前两种算法之间、但检索效率最高.
5 结束语
本文中提出了一个结合分块图像小波直方图和粒子群优化的新型图像检索方法.通过对粒子的速度和位置进行定义,将图像检索描述为一种组合优化问题,将自适应性粒子优化用于基于内容的图像检索,同时,粒子的重量由其自适应性确定.试验结果显示,该算法引入小波技术提高了特征提取的有效性;采用分块技术提高了图像检索性能;结合微粒群算法进行智能搜索加快了算法的执行速度.因此,BWPSOIR算法既解决了检索的准确率,同时又较好地完善了检索的速度问题,从而为大型图像数据库的智能图像检索问题提供了解决方案.
参考文献:
[1] Maurice Clerc,Kennedy James.The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J].IEEE Transactions on Evolutionary Computation,2002,6(1):58-73.
[2] Eberhart R C, Shi Y. Particle swarm optimization: developments, applications and resources[C].Proceedings of the IEEE Congress on Evolutionary Computation, 2001:81-86.
[3] 汪祖媛,梁栋,李斌.基于树状小波分解的纹理图像检索[J].中国图象图形学报,2001,6(11):1065-1069.
[4] Xie Chao, Wei Chengjian, xu Jun. Evolutionary wavelet-based similarity search in image databases[C]. IEEE Int Workshop VLSI Design & Video Tech,2005,(28/30):385-388.
[5] 史燕.基于小波变换的图像检索技术研究[D]. 西北大学,2006.
[6] 朱晓华.基于微粒群和小波变换的图像检索算法研究[D].华中师范大学,2008.
[7] Shi Y, Eberhart R.Empirical study of particle swarm optimization[C].Proceedings of the IEEE Congress on Evolutionary Computation,1999:1945-1950.
[8] Angeline P J.Evolutionary optimization versus particle swarm optimization: philosophy and performance difference[J]. Proceedings of the 7th International Conference on Evolutionary Programming Conference,Lecture Notes in computer Science,2003,3(1):601-610.

