干涉SAR卫星编队波束同步方法
贺东雷 曹喜滨 马骏 刘品雄
(1 中国空间技术研究院,北京100094)
(2 哈尔滨工业大学卫星技术研究所,哈尔滨150080)
1 引言
干涉SAR卫星编队为实现其功能,需考虑发射和接收卫星间的波束同步问题。目前,国内外有关波束同步的研究文献较少。文献[1]定性分析了天线波束指向对完成干涉SAR任务的影响;文献[2]讨论了轨道平行星载双站SAR系统的波束同步问题,为满足卫星在不同轨道周期内的幅宽重叠率要求,给出一种使测绘分辨率达最高的折衷方案;刘建平等提出了三种波束指向同步方法[3];黄海风等总结了波束指向同步一般方法,并提出一种基于波束指向同步的波束覆盖同步方法[4]。值得注意的是,在SAR数据处理中,多普勒中心频率受地球自转影响很大,给成像处理带来困难,通过对SAR卫星姿态进行偏航导引控制可有效解决这一问题[5]。综上所述,有必要研究满足偏航导引要求的干涉SAR卫星编队波束同步策略。
2 满足偏航导引要求的波束同步策略
当轨道偏心率为小量时,SAR卫星偏航导引律为[5]
式中 ωe为地球角速度;i为卫星轨道倾角;ωs为平均轨道角速度;u为近地点幅角。可见,偏航导引角随卫星在轨道上位置变化而变化,其周期与轨道周期相同,最大幅度约为4°,不能被轻易忽略。
一般情况下,SAR天线体积和质量较大,在卫星上安装方位固定。在本文研究中,主星偏航角按照式(1)所示规律变化,考虑如何采用调节从星姿态的方式实现主从星波束同步。
2.1 基于规划姿态角的波束同步策略
图1中,O1X1Y1Z1和O2X2Y2Z2是主从星轨道坐标系,Ns1和Ns2为与地心连线和地球表面交点,e为转轴单位矢量,γ为天线在星体中侧视安装角。两星本体坐标系与轨道坐标系重合时,天线波束覆盖区域如虚线椭圆所示。当主星存在偏航角α时(见图1),可基于下述步骤规划从星姿态:
1)调节从星俯仰姿态,使本体坐标系OX轴负方向指向N2(N2为主星波束绕其轨道坐标系O1Y1轴旋转后与从星轨道面交点);
2)调节从星偏航姿态,使天线俯仰主平面过波束中心点;
3)调节从星横滚姿态,使两天线波束照射中心重合。
设波束同步实现后,从星观测矢量在轨道坐标系中方向余弦为L=[l1 l2 l3]T,俯仰角为φ,偏航角为θ,天线相对于体坐标系横滚角为φ,基于φ-θ-φ的转动顺序有
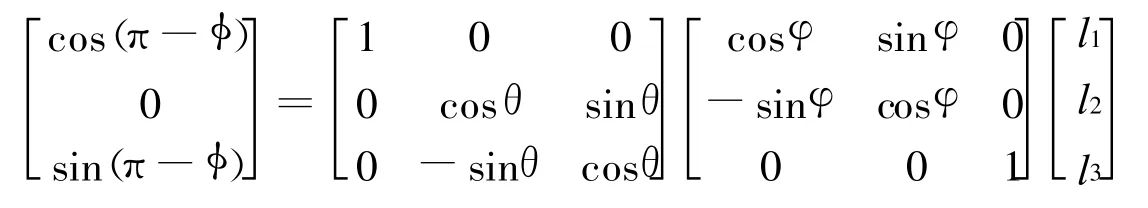
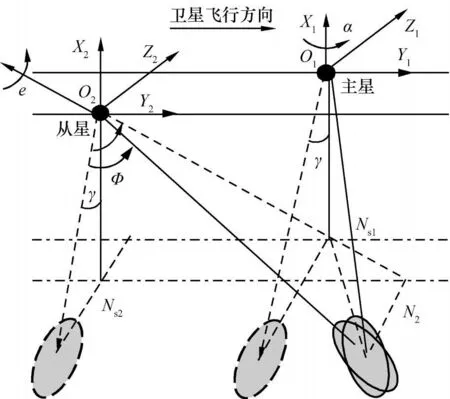
图1 双星编队波束覆盖同步示意图
若知道L和φ,从星偏航角θ和滚转角φ-γ为
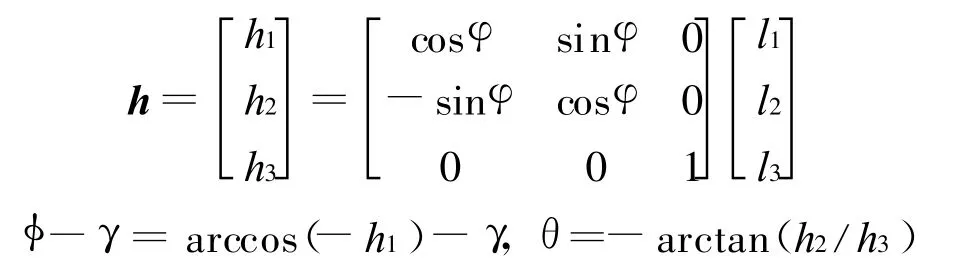
可见,先要求解出L=[l1 l2 l3]T和φ,具体方法如下。
(1)确定从星观测矢量在其轨道坐标系中的方向余弦L
设主星波束在其轨道坐标系中方向余弦为F,则有
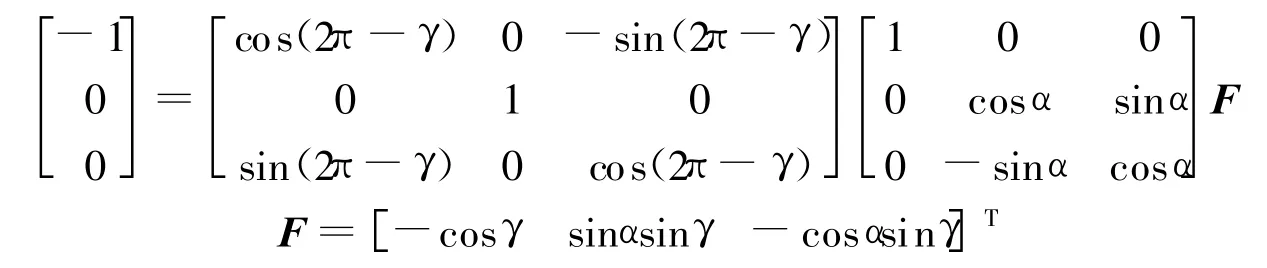
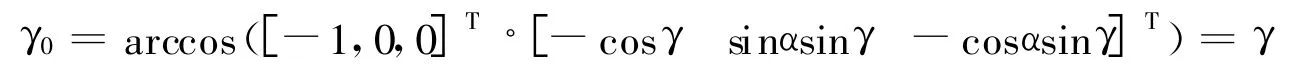
由余弦定理可得地面目标和主星间距离Rt(r和Re分别为主星地心距和地球半径)
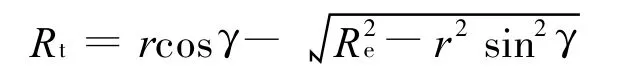
设地面目标B相对主星A的矢量为AB,在主星轨道坐标系中可表示为
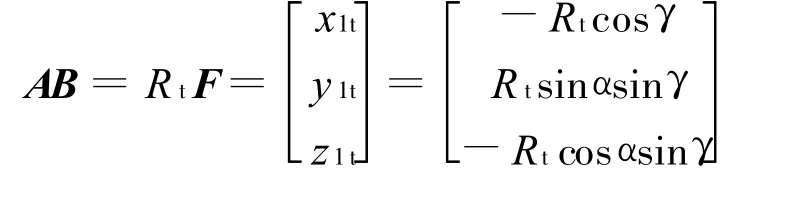
若主星A相对于地心O的矢量为OA,轨道到惯性坐标系的转换矩阵M1,则目标B相对于地心O的矢量OB在惯性坐标系中可表示为
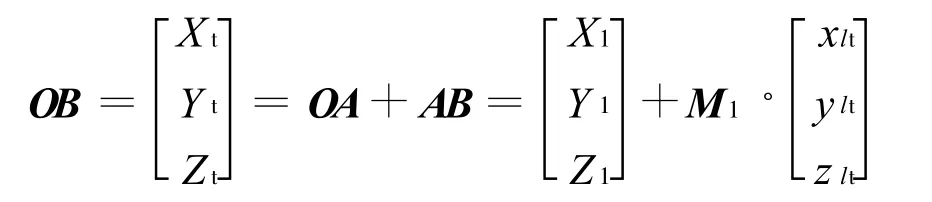
于是,从星波束在其轨道坐标系中位置矢量为(其中X2,Y2,Z2为从星惯性坐标,M2为从星轨道到惯性坐标系的转换矩阵)
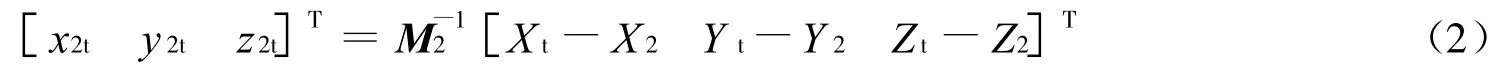
将上述矢量单位化,即可确定方向余弦L=[l1 l2 l3]T。
(2)确定从星机动俯仰角φ
首先,确定主星O1到N2(见图1)的位置矢量O1N2在主星轨道坐标系中的方向余弦设N2是主星波束绕其轨道坐标系O1Y1轴旋转ε角度后与从星轨道面交点,则有
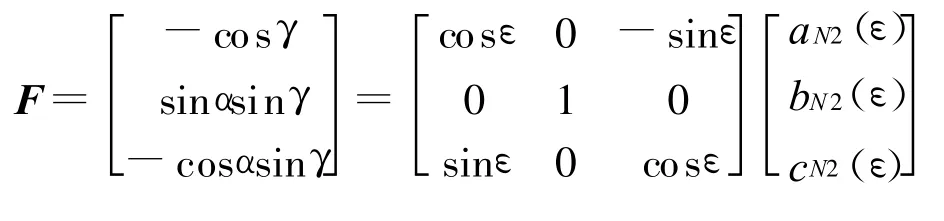
于是有
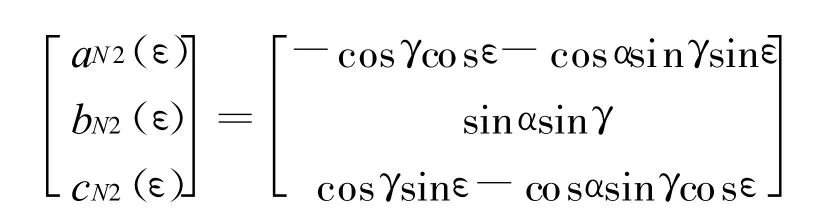
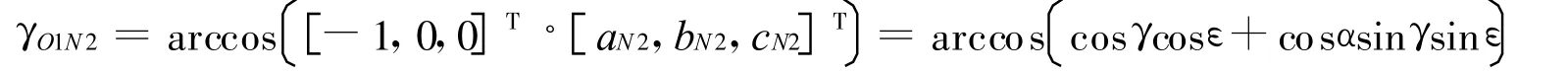
类似于AB长度求解方法,得矢量O1N2长度
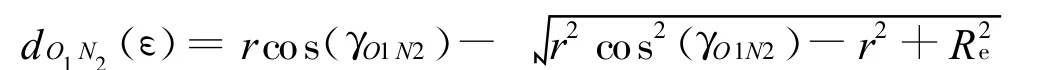
地心到N2的矢量ON2在地心惯性坐标系中可表示为
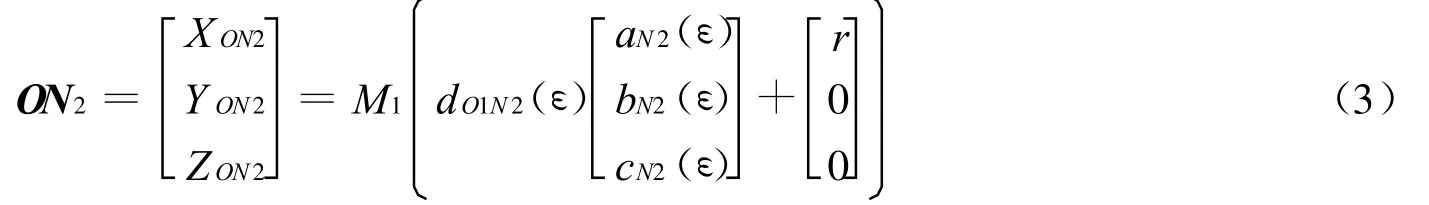
设从星轨道面法线在惯性坐标系中表示为G=M2[0,0,1]T,由于ON2与从星轨道面法线垂直,有
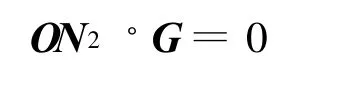
结合式(3)并整理得
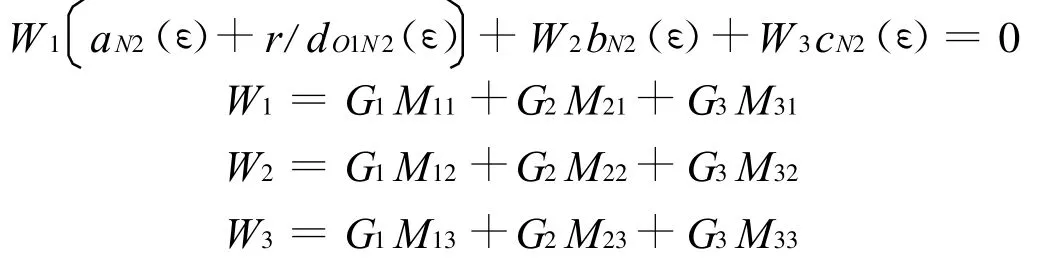
式中 Mij为矩阵M1的i行j列元素。
最终可整理为
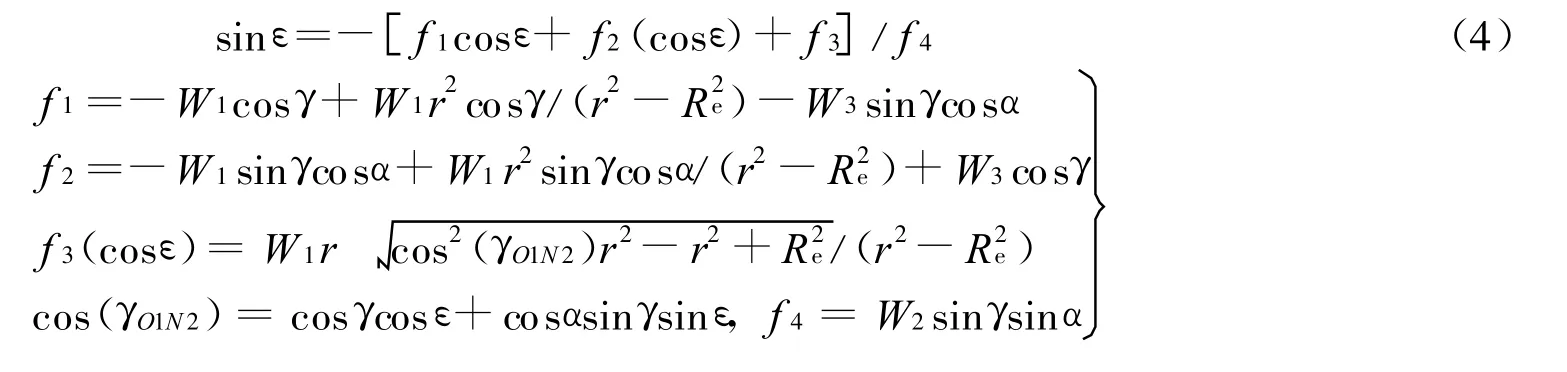
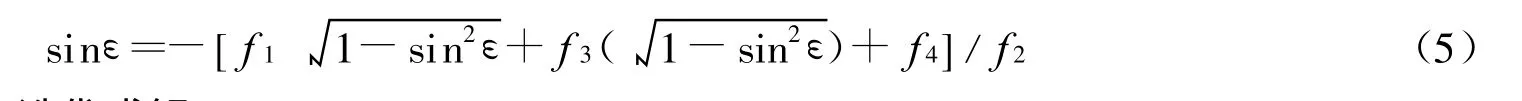
于是可基于式(5)迭代求解ε。
得到x之后,由式(3)可得O2N2在从星轨道坐标系中位置矢量
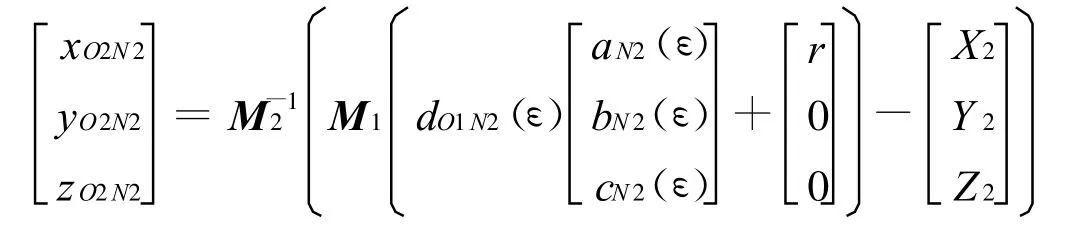
可得从星俯仰角
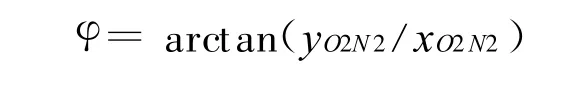
2.2 基于欧拉旋转的波束同步策略
第2.1节方法虽然直观,但需对应一定的姿态机动顺序进行抽象数学建模,且求解过程有些繁琐。为克服这个不足,下面研究基于欧拉旋转的波束同步策略。
初始时刻从星天线在轨道坐标系中位置矢量为
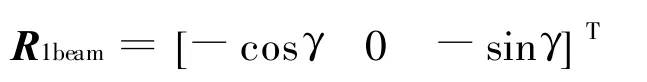
由式(2)可知当从星机动到目标姿态时,其波束在轨道坐标系中可表示为
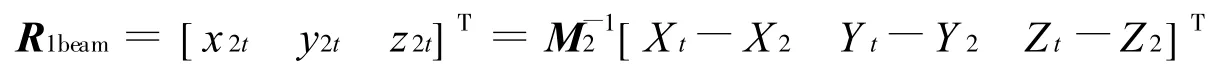
可得波束矢量从R1beam到R2beam的旋转欧拉参数
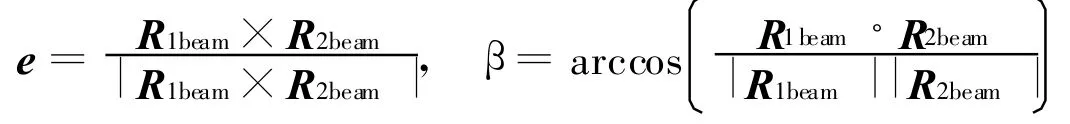
式中 e为转轴单位矢量;ex,wy,ez分别为矢量e在参考坐标系中的方向余弦;β为绕相应轴的转角。于是,可得以欧拉参数表示的坐标旋转矩阵A(e,Φ)。
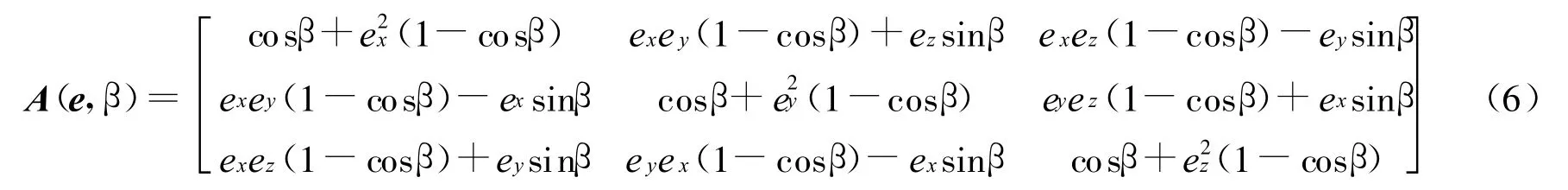
假设仍按俯仰角φ、偏航角θ、滚转角φ的3-1-2姿态旋转顺序,则以欧拉角表示的坐标旋转矩阵为
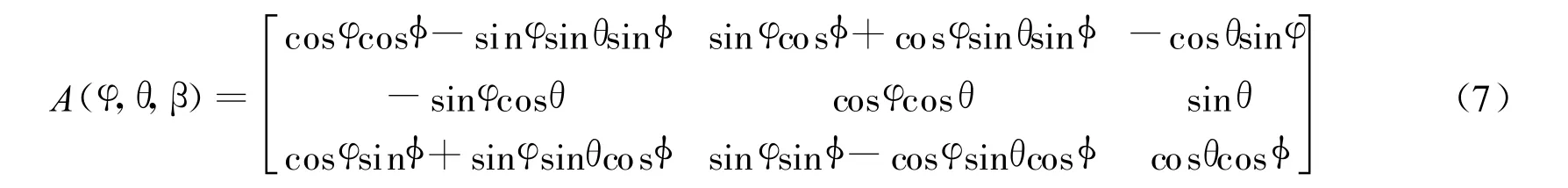
对比式(6)和式(7),可得俯仰角、偏航角、滚转角分别为
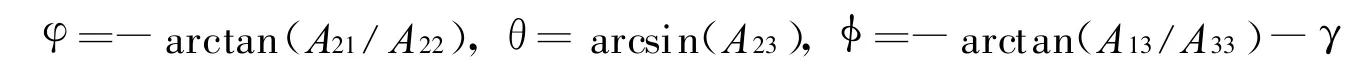
式中 Aij为矩阵A(e,β)中 i行j列元素。
3 数值仿真与结果分析
表1给出了编队卫星初始轨道参数,SAR天线在星体中安装角为右侧视35°,俯仰和方位向波束宽度分别为10m和3.5m。图2、3分别为两种方法的主从星偏航角对比曲线和从星三轴姿态角变化曲线。

表1 主从星初始瞬时轨道要素
图2 第一种波束同步方法姿态角变化曲线
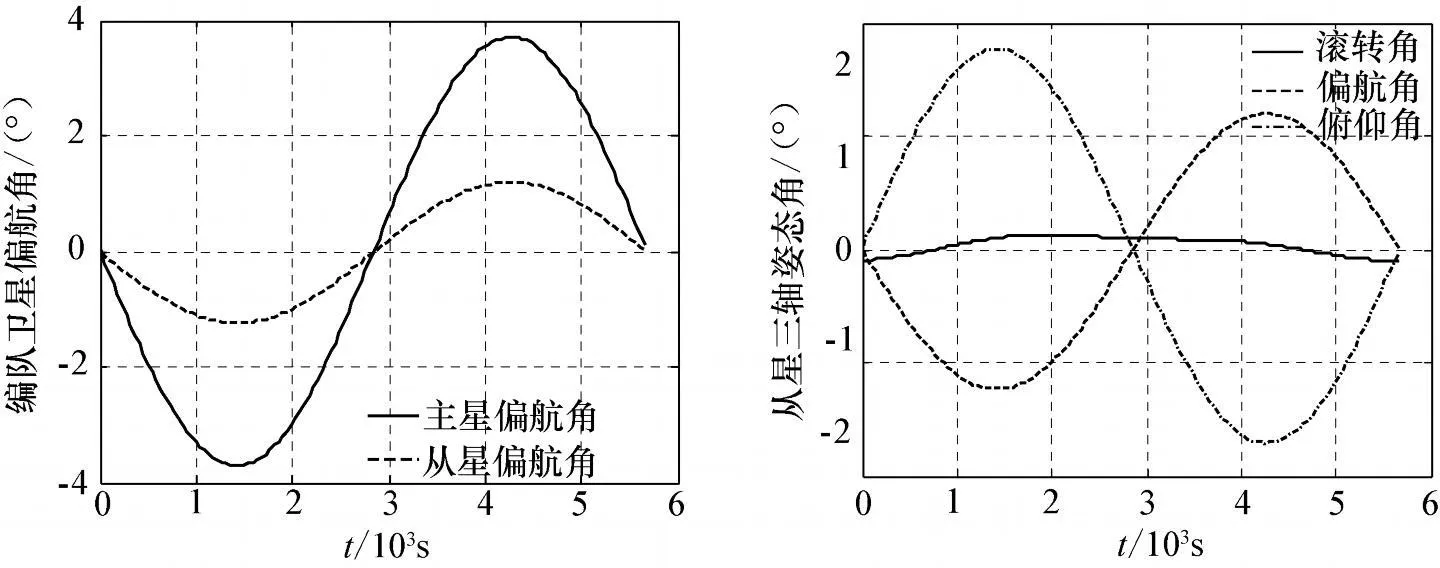
图3 第二种波束同步方法姿态角变化曲线
不失一般性地,当主星纬度为0°、81°时,仿真分析两种方法的波束同步效果,如图4、5所示。
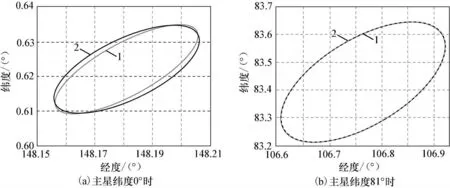
图4 第一种方法的波束覆盖同步效果
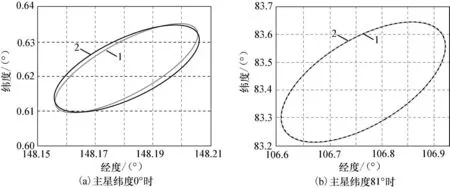
图5 第二种方法的波束覆盖同步效果
图6给出了主从星波束覆盖椭圆长半轴间夹角 Ψ的时间历程曲线。可见两种方法的夹角 Ψ均呈现周期性变化,且前者夹角 Ψ大于后者,即第二种方法波束覆盖同步效果较好。
4 结束语
仿真结果表明,从星偏航角变化趋势与主星类似,只是角度大小存在一定差异,可视为满足波束同步要求的从星偏航角;另一方面,当编队飞行于不同纬度区域上空时,本文两种方法均可有效实现波束覆盖同步,且第二种方法波束同步效果更好,证实了本文方法的正确性和有效性。
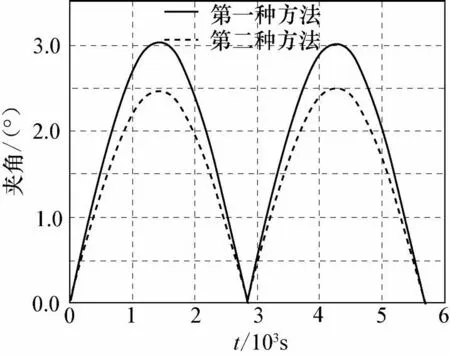
图6 夹角Ψ的时间历程曲线
[1] MASSONNET D.Capabilities and limitation of the interferometric cartwheel[J].IEEE Trans.On Geo.and Remoting Sensing,2001,39(3):506-520.
[2] MARCO D′ERRICO.Attitude and antenna pointing design of bistatic radar formations[J].IEEE Trans.On AES,2003,39:949-959.
[3] 刘建平,梁甸农.主星带分布式小卫星雷达系统的波束同步分析[J].国防科技大学学报,2006,28(2):54-58.
[4] 黄海风,梁甸农.非合作式星载双站雷达波束同步设计[J].宇航学报,2005,26(5):606-611.
[5] 孟云鹤,尹秋岩,戴金海.SAR卫星偏航导引补偿效果分析[J].国防科技大学学报,2005,25(5):18-21.
- 中国空间科学技术的其它文章
- “嫦娥二号”卫星发射及任务实施情况

