基于PLC的模糊控制在挤出机温度控制系统中的应用

吴 佳， 翁正新

(上海交通大学电子信息与电气工程学院，上海 200030)

基于PLC的模糊控制在挤出机温度控制系统中的应用

吴 佳， 翁正新

(上海交通大学电子信息与电气工程学院，上海 200030)

为了进一步提高挤出机温度控制性能，提出了一种以模糊控制为核心的温度控制系统。该系统能够很好地解决温度超调的问题，并能提高系统的控制精度和响应速度。同时结合可编程序控制器(PLC)来实现该控制系统，使其更为灵活及高效。

挤出机； 模糊控制； 温度控制； PLC

0 引 言

在挤出设备中，温度不但对产品的质量有最直接的影响，而且对加工稳定性、设备的耐用性等都有影响。如果挤出温度过高，橡胶容易产生焦烧现象，即发生早期硫化(交联)并失去流动性能和再加工的能力。而挤出温度太低，不但会使产品表面不光滑、容易脱节，而且会加剧螺杆与料筒的磨损，加重驱动系统的负载，甚至直接带来零部件的致命损伤[1]。在实际生产过程中，影响温度的因素比较多，包括：静液压功率、模头阻力、电加热器功率、聚合物导热性能、室温、冷却水温度及信号噪音等。

因此，在设计挤出机温度控制系统时很难建立精确的数学模型，在很多情况下，挤出过程的温度控制在很大程度上依赖于操作人员和工程师的经验来进行调整。本文则主要介绍了如何利用模糊控制方法对温度进行高精度控制的应用实例。

1 温度控制系统的工作原理

温度控制系统的控制对象是加热及冷却模块，它可用近似一阶惯性环节和滞后环节来描述，其传递函数为[2]：

G(s)=Ke-τs/(Ts+1)

(1)

式中，K为对象的静态增益；T为对象的时间常数；τ为对象的滞后时间；s为时间变量。

通常获得近似传递函数的方法是对控制对象施加阶跃输入信号，测得控制对象的阶跃响应，再通过阶跃响应曲线确定近似的传递函数。针对本文的控制对象，我们可以采用飞升曲线法进行实验，获得其飞升曲线，然后根据Cohn-Coon公式求出对象的参数。Cohn-Coon公式如下：

K=ΔC/ΔM

T=1.5(t0.632-t0.28)

式中，ΔM为系统阶跃输入幅值；ΔC为系统输出响应幅值；t0.28为对象飞升曲线在0.28ΔC时的时间(s)；t0.632为对象飞升曲线在0.632ΔC时的时间(s)。

经计算可得K=0.9，T=120 s，τ=38 s，代入式(1)可得传递函数为：

G(s)=0.9e-38s/(120s+1)

本温度控制系统通过温度传感器采样得到挤出机机身各温区的实际温度，并送至可编程控制器(PLC)。PLC将实际温度值PV与设定温度值SP进行比较，并将得到的结果送入温度控制器，温度控制器按一定的控制规则计算出相应的控制量MV，以控制固态继电器和冷却水比例电磁阀，从而实现对温度的控制。

其中温度控制器将直接影响到整个系统的控制精度。常规比例、积分、微分(PID)控制具有简单、稳定、可靠等优点，特别适用于线性、定常、时不变系统，但其依赖系统模型，对时变参数敏感；而模糊控制器具有控制灵活、适应性强的优点。针对挤出机温度控制系统的数学模型无法精确建立的情况，本文选用模糊控制器作为温度控制器，以求达到更好的控制效果。

2 模糊控制器设计

根据温度控制的结构特点，以温度设定值和温度实际值之间的误差值e和误差变化率ec作为输入，通过模糊化、模糊推理以及去模糊化后，得到需要的输出量u。在加热状态下(即获得正的输出量u)，PLC根据不同的u值输出相应频率的脉冲信号，以控制继电器的通断时间。在冷却状态下(即获得负的输出量u)，PLC则输出0～10 V直流电压信号给比例阀，使比例阀输出0～100%的开度，以控制冷却功率。

本文选用二维模糊控制器，拥有双输入和单输出，其结构如图1所示。模糊控制器的实现方法是将模糊控制规则离线转化为模糊控制表并输入PLC，并在每个采样周期内在线查询获得输出量。同时，输入的模糊化和输出的去模糊化也在PLC中完成。

图1 模糊控制器结构图

模糊控制器输入e和ec采用离散差分的表达方式，即：

e(k)=PV(k)-SP

式中，PV为瞬时实际温度值；SP为设定温度值；T′为采样周期；k为时间变量。

综合考虑了该系统的稳态精度、稳定性和动态性的要求后，本文将e、ec和u的模糊子集定为7级，增加分级档数，可以提高稳态精度，但同时也将扩大模糊关系矩阵的维数，增加控制表的容量，这对提高控制稳定性和快速性是不利的[3]。

e，ec，u={NB，NM，NS，O，PS，PM，PB}

子集中的元素分别代表负大，负中，负小，零，正小，正中，正大。

e，ec在模糊集上的论域定为：

e,ec={-6,-5,-4,-3,-2,-1,0,+1,+2,+3,+4,+5,+6}

u在模糊集上的论域定为：

u={-7,-6,-5,-4,-3,-2,-1,0,+1,+2,+3,+4,+5,+6,+7}

据对温度控制系统多次手动调节得出的经验，将温度误差e的基本论域定为[-20°C，+20°C]，温度误差的变化率ec的基本论域定为[-1°C/s，+1°C/s]，并将所有越限值按边界值进行处理。

本文中e，ec，u的隶属度函数均采用高斯正态分布函数(见图2和图3)。

图2 误差e、ec的隶属度函数

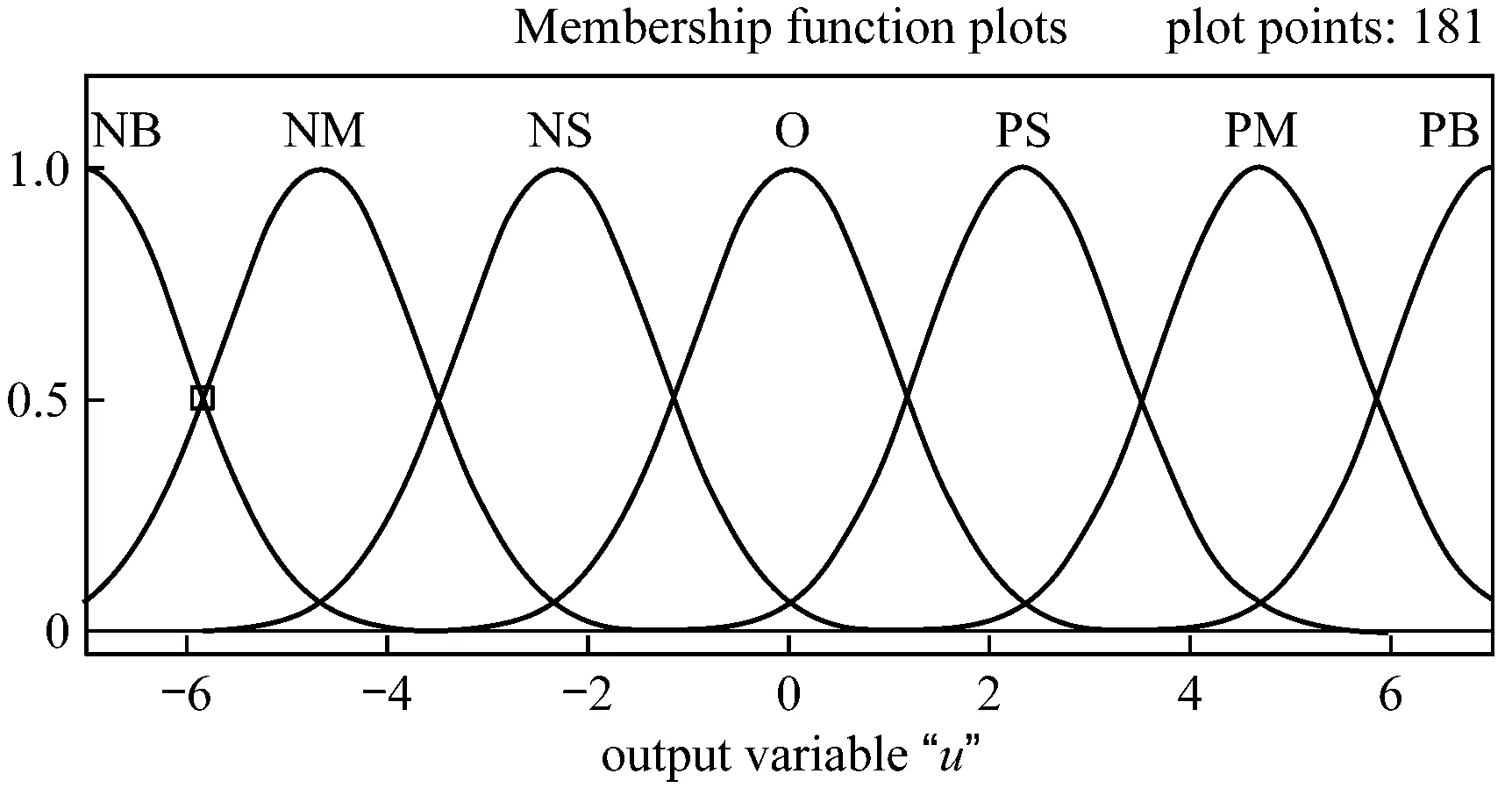
图3 输出u的隶属度函数

经过分析挤出机的温度变化特性，可以总结出部分控制经验，比如“实际温度比设定温度低很多，且温度降低得很快时，需要输出非常大的加热控制量”，“实际温度比设定温度高很多，且温度降低和很慢时，需要输出非常大的冷却控制量”，因此将这些模糊控制规则归纳为模糊控制规则表，见表1。再按最大隶属度原则得出控制量表，见表2。

表1 模糊控制规则表

注：E、EC分别为精确量e、ec的模糊量。

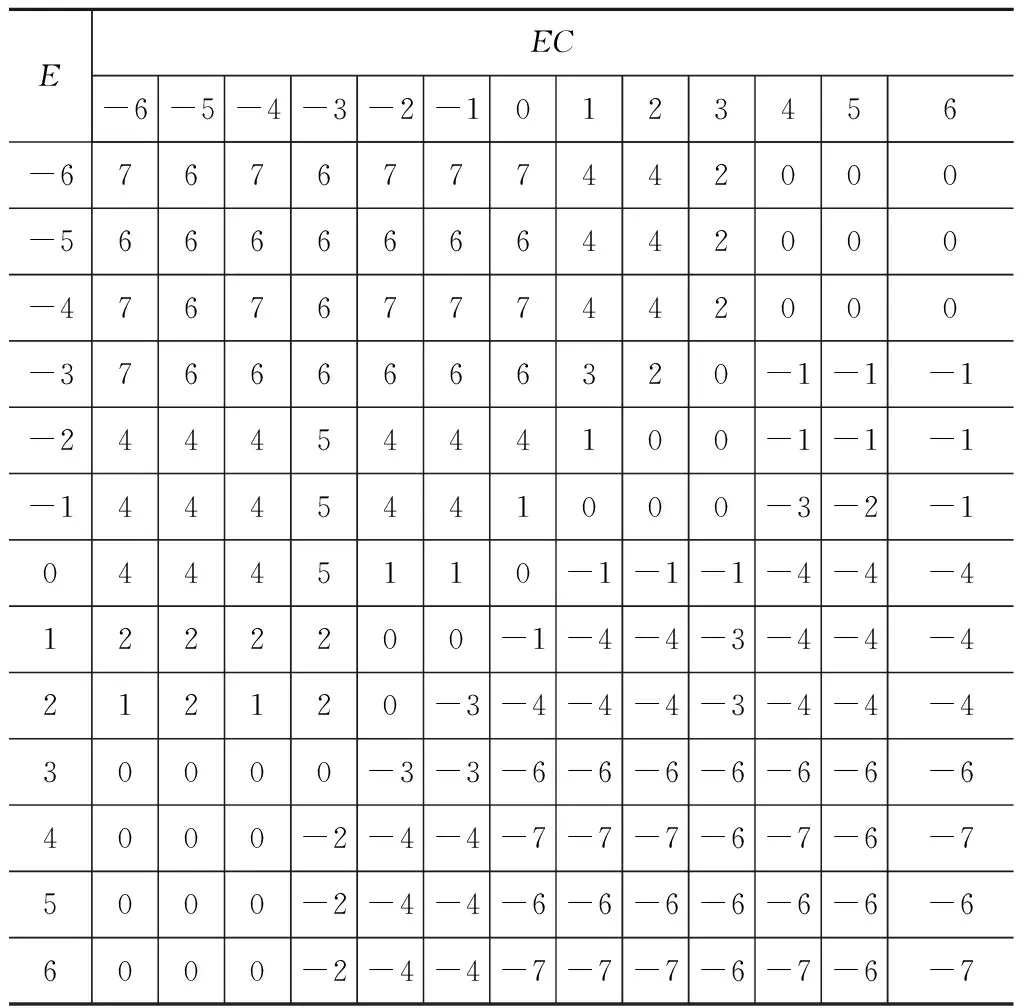
表2 控制量表

3 模糊控制器的PLC编程

本文的控制系统采用西门子STEP7作为软件编程环境，使用模块化编程方式。主要程序包括e(温度偏差)和ec(偏差变化率)的计算；精确量e、ec到模糊量E、EC的转换；模糊控制量表的查询；模糊控制量U到精确控制量u的转换。

其中模糊控制量表的查询程序是整个程序的关键。离线建立的模糊控制量表，按照从上到下、从左到右的顺序输入到相应的DB3数据块中。在每个采样周期时，根据得到的误差和误差变化的论域元素，在线查得模糊控制量[4]。

该程序采用指针寻址方法。将输入模糊论域的元素[-n,n]转化为[0,2n]，即E,EC的值转化为[0，12]。控制量U的基址为0，偏移地址方程为4×(E+13EC)。具体程序如下。

Network 1：计算出U在表中的绝对地址，并存放在临时变量d4中。

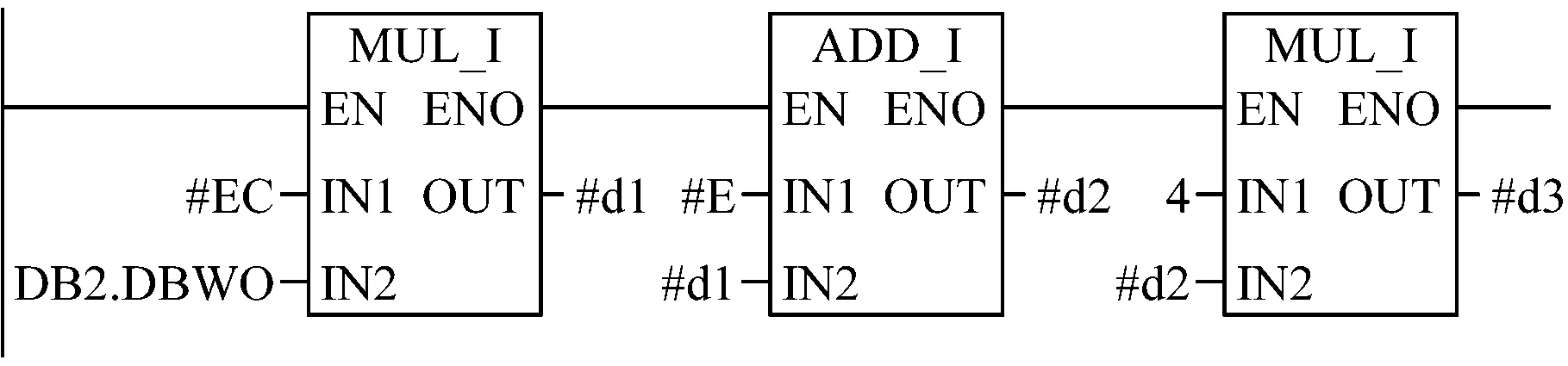
Network 2：

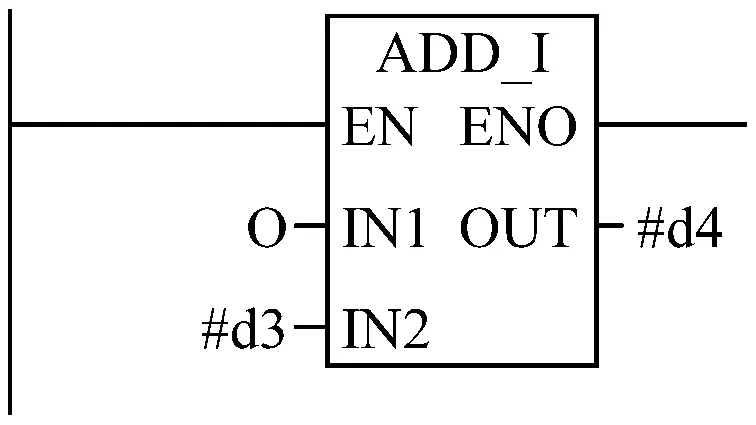
Network3：指针寻址，并将按地址查询到的数值存放在MD10中。

4 实验结果分析

图4为分别采用模糊控制器和常规PID控制器的温度曲线图。图中曲线1为模糊控制器的温度曲线，曲线2为PID控制器的温度曲线。从图中可以看出，模糊控制的温度曲线相比常规PID控制器的温度曲线，有更快的温升速度，超调量也更加小，后期也比较稳定，没有振荡出现。

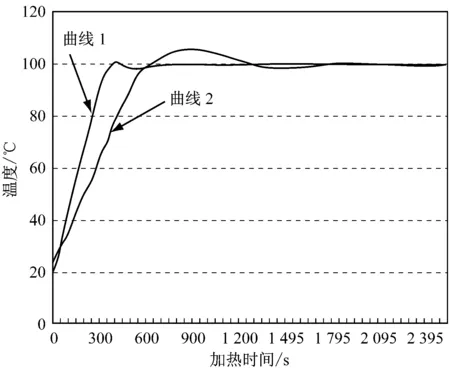
图4 两种不同控制器的温度曲线

5 结束语

本文利用模糊控制器对挤出机温度控制系统进行改良，并结合现有PLC进行软件实现，不仅提高了控制精度，而且并没有增加过多的硬件成本，取得了较为满意的效果。

[1] 梁 毅，费敏锐.单参数模糊PID在塑料挤出机温度控制系统中应用[J]. 华东理工大学学报(自然科学版)，2006(7)：840-843.

[2] 覃 强.模糊PID温度控制方案的仿真优选及其实现[D].北京：中国科学院电工研究所，2002.

[3] 张 宇.电加热器的模糊控制及其PLC实现[D].南昌：南昌大学，2005.

[4] 田 媛.PLC先进控制策略研究与应用[D].北京：北京化工大学，2005.

ApplicationofthePLC-BasedFuzzyControlintheTemperatureControlSystemoftheExtruder

WU Jia, et al

(Shanghai Jiaotong University, Institute of Electronic Information and Electrical Engineering, Shanghai 200030, China)

In order to improve temperature control of the extruder, a temperature control system focusing on fuzzy control was presented. This system can eliminate effectively overshoot and improve control precision and response speed of the system. Integration with programmable logic controller (PLC) improves flexibility and function of the system.

extruder; fuzzy control; temperature control; PLC

TM205.2

A

1672-6901(2010)05-0033-04

2010-02-11

吴 佳(1981-)，男，在读硕士研究生.

作者地址：上海市浦东新区凌河路777弄38号201室[200129].