材料弹性模量的仪器化压入测试方法

马德军

材料弹性模量的仪器化压入测试方法

马德军

(装甲兵工程学院 机械工程系，北京 100072)

应用量纲定理和有限元方法对仪器化压入响应进行分析，同时引入联合弹性模量(Εc)来精确表示压头与被压材料的综合弹性效应。结果表明：名义硬度Hn和联合弹性模量Εc的比值与卸载功We和压入总功Wt的比值间存在近似的函数关系。基于上述关系，提出由名义硬度和压入比功确定材料弹性模量的新方法，同时分析该方法的理论误差，验证结果表明该方法较传统Oliver-Pharr方法具有更高的测试精度。

弹性模量；仪器化压入；硬度；压入功；有限元方法

随着表面改性材料、薄膜材料、MEMS(微电子微机械系统)材料、复合材料和纳米材料等领域的快速发展，表面、界面及微尺度材料的工作可靠性由于面临苛刻工作条件的挑战，越来越引起人们的重视，成为国内外研究的热点。然而，受尺寸限制，传统的材料力学性能测试技术及手段已经无法满足上述材料的力学性能测试需要，使得材料微区力学性能的测试成为亟待解决的关键问题。

仪器化压入技术是在传统布氏硬度和维氏硬度试验基础上发展起来的一种微区和非破坏性的新材料力学性能测试技术，它可以高精度地同步测试和记录各种几何形状的压头压入试样及撤离试样时的载荷与位移数据，从而可以提供比传统硬度试验更多的反映被测试材料力学性能的有用信息，这为材料诸多基本力学性能参数的识别提供了重要的技术手段[1−16]。1992年，美国商用仪器化纳米压入仪的发明人OLIVER 与Rice大学教授PHARR共同提出著名的基于仪器化压入测试技术确定材料弹性模量的经典方法，即Oliver-Pharr方法[17−19]。尽管该方法目前已经在各类商用仪器化压入仪中获得广泛使用，但该方法应用于低硬化水平的被测材料时，可以导致被测材料的弹性模量严重偏离其真值。因此，精度不高是目前各类商用仪器化压入仪存在的突出问题。

针对上述问题，本文作者应用量纲定理和有限元方法对仪器化压入响应进行分析，进而提出基于名义硬度和压入比功确定材料弹性模量的新方法。

1 仪器化压入问题的量纲和有限元分析

在仪器化压入实验中，三棱锥Berkovich 压头获得广泛应用。与传统四棱锥 Vickers压头相比，三棱锥Berkovich 压头的优点在于可以避免压头尖端出现横刃，从而避免在浅压入时失去几何自相似的特性。研究表明，就仪器化压入加、卸载曲线而言，Berkovich压头可以用具有相同面积—深度关系的锥半角为70.3°的圆锥压头来近似，亦即对于同一被压材料，采用 Berkovich 压头和采用锥半角为 70.3°的圆锥压头可以获得相同的仪器化压入加载、卸载曲线[20−21]。因此，考虑建模简单，本文作者只就材料在锥半角为70.3°的圆锥压头作用下的压入响应展开分析。

图1所示为典型的仪器化压入载荷—位移曲线。根据该曲线可以定义名义硬度Hn为最大压入载荷Fm与对应最大压入深度 hm时的压头横截面积 A(hm)之比，即，Hn≡Fm/A(hm)，此外，定义压入加载功 Wt和卸载功 We分别为压头在加载过程和卸载过程中所做的功，其值分别等于加载曲线和卸载曲线与载荷—位移曲线横坐标所围面积，如图1所示。

由于仪器化压入问题涉及复杂的材料、几何和接触边界条件非线性，因此，人们至今无法获得准确的解析解，对此本文作者采用有限元数值方法来分析被压材料参数与压入响应间的关系。假设被压材料为均匀、各向同性、率无关固体，且遵循Von Mises 屈服准则和纯各向同性强化准则；同时假设被压材料的单轴应力—应变关系由线弹性与 Hollomon 幂硬化函数组成，即

图1 仪器化压入加载、卸载曲线及加载功、卸载功示意图Fig.1 Schematic diagram showing indentation loading curve,loading work, unloading curve and unloading work in instrumented test

式中：σ和ε为真应力和真应变；σy和εy=σy/Ε为屈服应力和屈服应变；n为应变硬化指数。因此，当假设压头为弹性体、压头与被压材料间无摩擦时，任何压入响应均可以表示为被测材料的屈服强度σy、硬化指数n、弹性模量 Ε、泊松比 ν、金刚石压头的弹性模量Εi、泊松比νi以及最大压入深度hm的函数。在此，将名义硬度Hn和压入比功We/Wt当成压入响应，那么它们可以分别表示为如下函数：

式中：Ε/(1−ν2)和 Εi/(1−νi2)分别是被测试材料和压头材料的平面应变弹性模量[22]，比值[Ε/(1−ν2)]/ [Εi/(1−νi2)]被定义为平面应变弹性模量之比，用 η表示，即，η=[Ε/(1−ν2)]/ [Εi/(1−νi2)]。考虑到在弹性接触问题分析中广泛使用压头及被压材料的折合弹性模量Εr[22]，且Εr=1/[(1−ν2)/Ε+(1−νi2)/Εi]，因此，Εi/(1−νi2) 可以表示为 Εi/(1−νi2)=1/[(1/Εr)-(1−ν2)/Ε]，同时式(2)和(3)可以分别改写为

应用量纲∏定理，式(4)和(5)可简化为

由于[Ε/(1−ν2)]/Εr=[Ε/(1−ν2)][(1−ν2)/Ε+(1−νi2)/Εi]=1+[Ε/(1−ν2)]/[Εi/(1−νi2)]，式(6)和(7)可以被进一步表示为

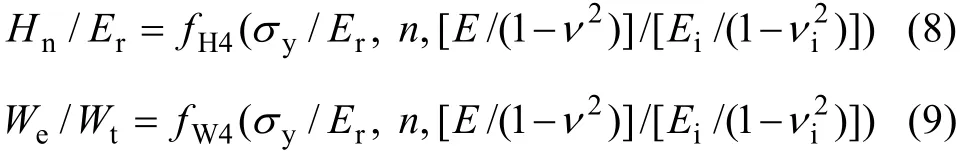
根据式(9)，σy/Εr可以表示为

将式(10)代入式(8)，最终可以确定 Hn/Εr为 We/Wt、n 和[Ε/(1−ν2)]/[Εi/(1−νi2)]的函数，即

为获得式(11)的显式解，应用商用有限元软件ABAQUS[23]对圆锥压头(圆锥半角为 70.3°)压入弹塑性材料的载荷—位移响应进行了有限元数值模拟，图2所示为有限元划分的压头与被压材料总体网格和靠近压头尖端的局部网格。其中，对压头与被压材料分别划分了2 500和8 100个轴对称四边形单元，上述网格的划分可以保证在压头达到最大压入深度时压头的横截面半径小于被压材料的径向和高度总体尺寸的1/40，同时接触单元数目不低于30个。为检验所划分网格的收敛性，在加密网格数一倍情况下，将有限元计算所得最大压入载荷和比功与原网格结果进行比较，发现其变化不超过0.5%，表明该方法划分的有限元网格具有收敛性。在有限元模拟中，屈服强度的取值范围为 0.5～160 000 MPa，硬化指数的取值为 0、0.15、0.30和 0.45，平面应变弹性模量之比η=[Ε/(1−ν2)]/[Εi/(1−νi2)]的取值为 η1=[70/(1−0.302)]/∞=0、η2=[70/(1−0.302)]/[1 141/(1−0.072)]=0.067 1、η3=[200/(1−0.302)] /[1 141/(1− 0.072)]=0.191 7 和 η4=[400/(1−0.302)]/[1 141/(1−0.072)]= 0.383 4。图3所示为对应不同的η和n时的Hn/Εr与We/Wt关系。从图3中可以看出，对于确定的平面应变弹性模量之比 η，所有数据点均分布在以n=0和n=0.45为上、下边界的狭窄带里，因此，为方便应用可以忽略硬化指数 n对 Hn/Εr与We/Wt关系的影响，而将Hn/Εr与We/Wt关系近似表示为一一对应的函数关系，本文作者称该关系为代表性的Hn/Εr—We/Wt关系，通过采用6次多项式对数据点进行曲线拟合，可以方便地确定上述代表性关系，结果如图 3(a)～(d)所示。进一步将 4个平面应变弹性模量之比 η：η1、η2、η3和 η4所对应的 4个代表性的Hn/Εr—We/Wt关系放入图4中进行比较发现，不同的η对代表性的Hn/Εr—We/Wt关系尚存在影响，表明在弹性接触问题分析中广泛使用的压头及被压材料的折合弹性模量 Εr并不能精确反映压头及被压材料的联合弹性效应，否则η对代表性的Hn/Εr—We/Wt关系将不构成影响。为了在名义硬度Hn、压入比功We/Wt和压头及被压材料平面应变弹性模量 Εi/(1−νi2)和 Ε/(1−ν2)间建立起不受参数η 影响的单一函数关系，本文作者定义压头及被压材料的联合弹性模量为Εc≡1/[(1−ν2)/Ε+1.32(1−νi2)/Εi]= Εr/[1+0.32η/(1+η)]，同时用 Εr=Εc[1+0.32η/(1+η)]代替代表性 Hn/Εr−We/Wt函数关系中的Εr，则容易确定对应于4个平面应变弹性模量之比(η)：η1、η2、η3和 η4的 4 个代表性的Hn/Εc−We/Wt，结果如图5所示。显然上述4个代表性的 Hn/Εc−We/Wt关系趋于一致，这说明 η的取值对Hn/Εc−We/Wt函数关系的影响很小。因此，可以用一个单一的6次多项式来代表上述函数关系，即

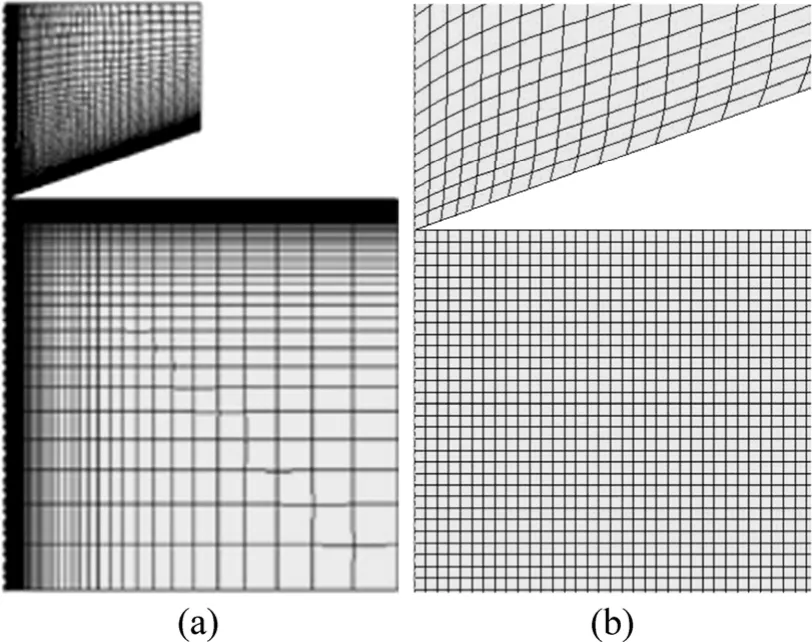
图2 压头与被压材料有限元(a)总体网格(b)靠近压头尖端的局部网格Fig.2 Finite element mesh design for conical indenter and indented solid: (a) Overall mesh; (b) Mesh near contact region

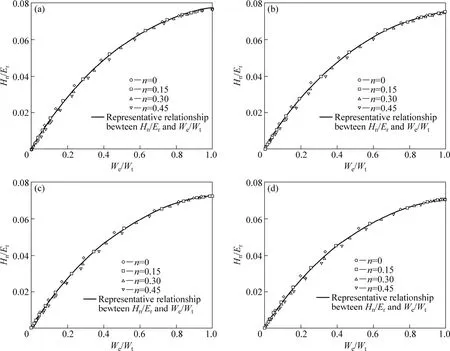
图3 对应η和n不同取值下的Hn/Εr—We/Wt关系Fig.3 Plots of Hn/Εr versus We/Wt with different values of n for four cases specified by η=0 (a), η=0.067 1 (b), η=0.191 7 (c) and η=0.383 4 (d)

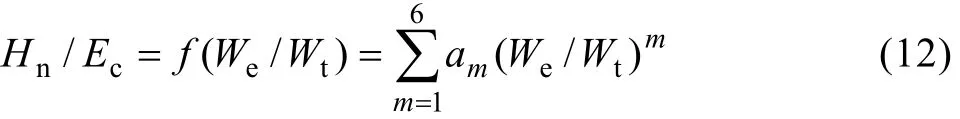
式中：a1=0.170 204, a2=−0.157 669, a3=0.110 937,a4=−0.048 401, a5=−0.005 516 和 a6=0.007 625。

式(12)的建立揭示了名义硬度Hn、压入比功We/Wt和压头及被压材料联合弹性模量Εc间的函数关系，为仪器化微米压入测试材料弹性模量奠定了理论基础。

图4 对应不同η取值下Hn/Εc与We/Wt关系Fig.4 Relationships between Hn/Εc and We/Wt corresponding to different elastic modulus ratios

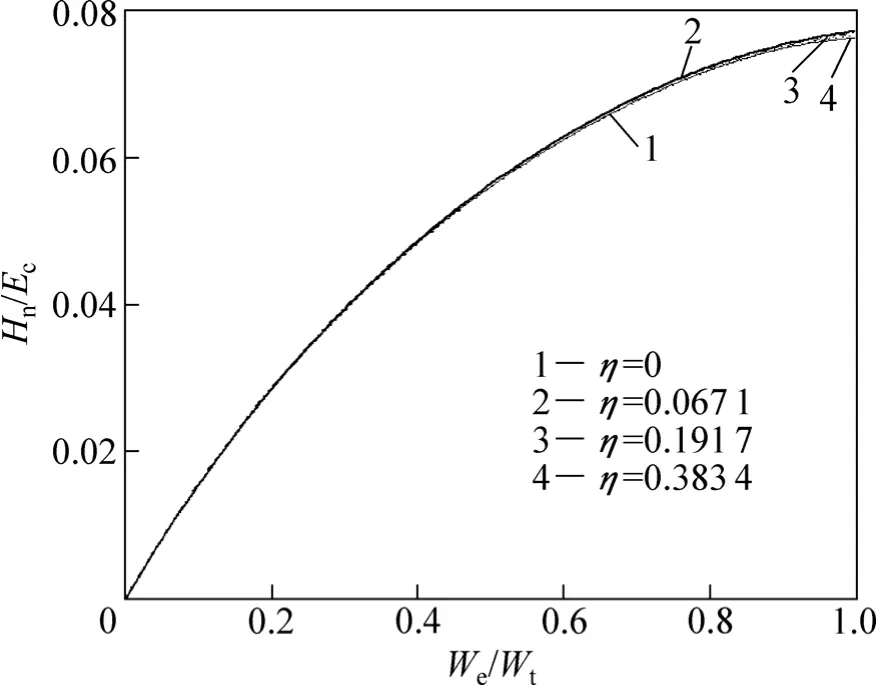
图5 对应不同η取值下Hn/Εr和We/Wt关系Fig.5 Relationship between Hn/Εc and We/Wt corresponding to different elastic modulus ratios

2 弹性模量的测试方法

基于式(12)，本文作者提出确定材料弹性模量的一般方法，该方法由以下步骤组成。

1) 利用仪器化压入仪和金刚石锥形压头(Berkovich压头、Vickers压头或圆锥半角为70.3°的圆锥压头)对被测试材料表面实施最大压入深度 hm大于1 μm(hm≥1 μm)的垂直压入，获得被测试材料的载荷−位移曲线。

2) 根据被测试材料的载荷—位移曲线计算名义硬度 Hn≡Fm/A(hm)。其中，当 hm≥3 μm 时，A(hm)=24.52mh ，而当 1 μm≤hm≤3 μm，A(hm)应根据压头的面积函数来确定。

3) 通过分别积分加载曲线和卸载曲线计算压入加载功 Wt、卸载功 We，并在此基础上计算压入比功We/Wt。

4) 计算压头及被压材料的联合弹性模量 Εc=Hn/并最终确定被测试材料的弹性模量Ε=(1−v2)/[1/Εc−1.32(1−vi2)/Εi]。其中，金刚石压头的弹性模量为Εi=1141 GPa, 泊松比为vi=0.07, 被测试材料的泊松比可根据材料手册确定，如果手册不能确定，建议对金属材料取v=0.3,对陶瓷材料取v=0.2。

3 弹性模量测试方法的精度

如 果 用 (Hn/Εc|n=0， We/Wt|n=0)和 (Hn/Εc|n=0.45，We/Wt|n=0.45)分别代表 n=0和 n=0.45情况下的所有Hn/Εc−We/Wt数据点，那么在 We/Wt已知前提下，由式(12)确定压头及被压材料联合弹性模量Εc的最大理论相对误差δc+和δc−可以分别表示为

图6所示为测试联合弹性模量Εc的最大理论相对误差 δc+和 δc−随 We/Wt的变化。由图 6可以看出，两者的绝对值几乎相等，且随 We/Wt的增大最大理论相对误差δc+和δc-均减小。通过数据拟合可以用函数δc=δc(We/Wt)来表示 δc+和 δc−随比功 We/Wt的变化情况，即

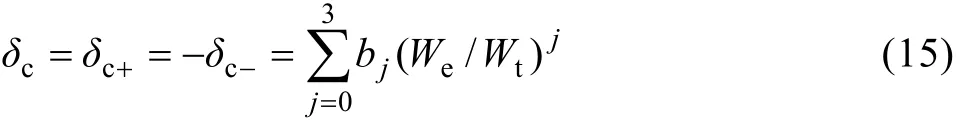
式中：b0=0.132 534，b1=−0.257 717，b2=0.126 525,b3=0.008 246。当We/Wt→0时，最大理论相对误差δc+和δc−均达最大，分别为13.25%和−13.25%，因此，从工程应用的角度讲上述精度基本可以满足测试要求。根据 δc可以进一步估计确定材料弹性模量的最大理论相对误差δ+和δ−分别为

图6 测试联合弹性模量 Εc的最大理论相对误差 δc+和 δc−随We/Wt的变化Fig.6 Change of maximum theoretically relative error δc+and δc− for determining combined elastic modulus Εc with We/Wt

显然，弹性模量的测试误差δ+和δ−不仅与We/Wt有关，而且还与联合弹性模量Εc或被测试材料的弹性模量Ε有关(金刚石压头的弹性模量 Εi和泊松比vi为定值)，分析式(16)和(17)可以发现，随We/Wt增大，最大理论相对误差 δ+和 δ−均减小；而随联合弹性模量Εc或被测试材料的弹性模量的增大，最大理论相对误差 δ+和 δ−均增大。

4 弹性模量测试方法的实验验证

首先利用 DAO等[20]发表的仪器化微米压入实验数据来检验本文作者所提方法的有效性。测试材料为两种铝合金，即 6061−T6511和 7075−T651。它们的弹性模量通过标准单轴拉伸试验被分别确定为66.8和70.1 GPa。实验对每种材料固定最大压入载荷并且重复 6次实施仪器化压入测试。根据实验所得载荷−位移曲线，同时应用所提材料弹性模量的确定方法和步骤,本文作者可以确定被测试材料的名义硬度Hn≡Fm/A(hm)、压入比功We/Wt、压头及被压材料的联合弹性模量并最终确定被测试材料的弹性模量 Ε=(1−v2)/[1/Εc−1.32(1−vi2)/Εi]。其中，金刚石压头的弹性模量为Εi=1 141 GPa, 泊松比为vi=0.07；两种被测试材料的泊松比均为0.33。将被测试材料弹性模量的测试结果与其已知值进行比较，可以确定其相对测试误差，表1和2所列为上述所提各参量的测试结果及弹性模量的测试误差。为便于比较，表中同时给出了由传统 Oliver−Pharr方法确定的弹性模量结果，表中用ΕO&P表示。从表1和2可以看出，对两种材料应用该方法获得的弹性模量测试结果均值与其已知值的相对误差分别为2.0%和−0.4%，而由传统Oliver−Pharr方法确定的弹性模量的均值相对误差分别为17.5%和13.0%,测试结果表明该方法是可行和非常有效的。此外，利用式(16)和(17)以及We/Wt和被测材料弹性模量Ε的均值，可以估计应用该方法测试上述两种铝合金材料弹性模量的最大理论相对误差± δ+=±δ-分别为±11.7%和±10.2%，显然实际测试结果的相对误差2.0%和−0.4%均在上述最大误差范围内。

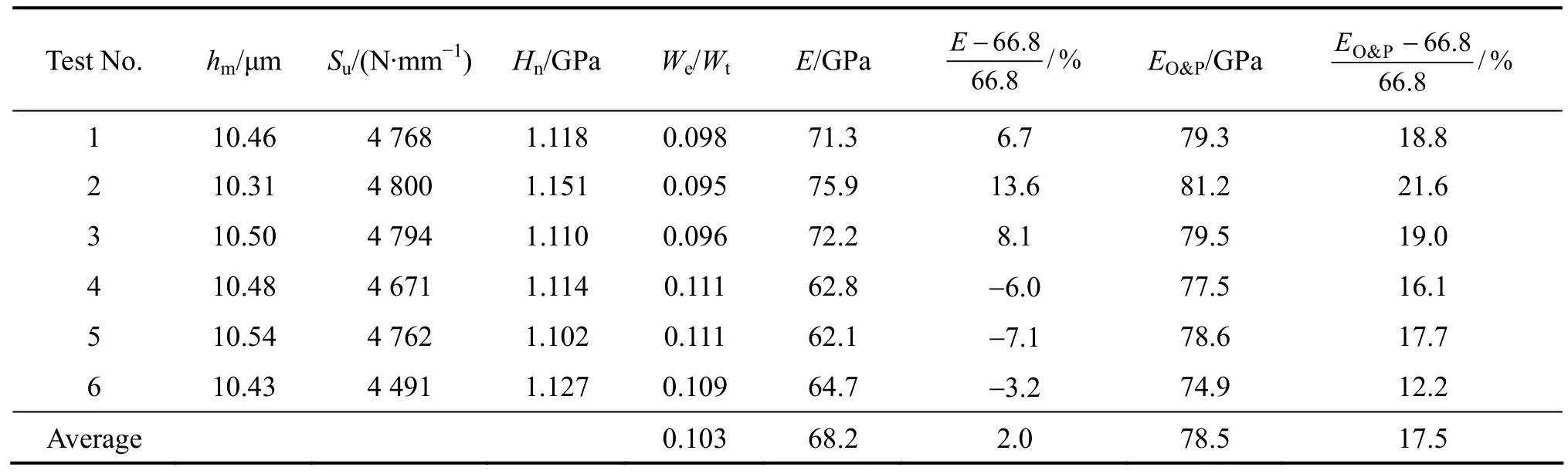
表1 铝合金6061−T6511的弹性模量仪器化压入测试结果Table 1 Values of Ε and ΕO&P for 6061−T6511 aluminum alloys determined from present method and Oliver & Pharr method

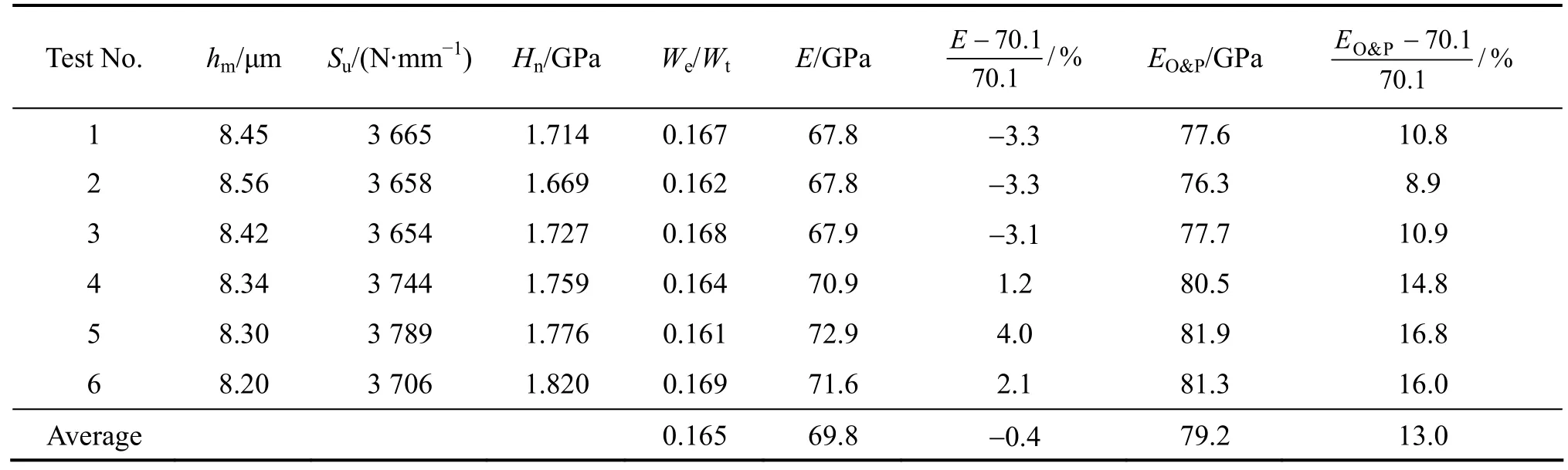
表2 铝合金7075−T651的弹性模量仪器化压入测试结果Table 2 Values of Ε and ΕO&P for 7075−T651 aluminum alloys determined from present method and Oliver & Pharr method

其次，选择铝单晶、滚动轴承钢GCr15和熔融硅3种材料进行仪器化微米压入实验，其中，铝单晶和熔融硅系美国 MTS公司提供的标准试样，已知其弹性模量分别为70.4 GPa和72 GPa，泊松比分别为0.347和0.170；滚动轴承钢GCr15系标准硬度块, 泊松比为0.29，其弹性模量采用标准超声波方法测量，结果为204 GPa。实验所用仪器为美国MTS公司生产的商用纳米压入仪(Nano Indenter®XP (MTS Systems Corp.,Knoxville, TN)),仪器配备的压头为金刚石 Berkovich压头，其面积函数为；A(h)=24.497 4h2+424.149h+28 211.4h1/2−69 751.1h1/4−46 333.3h1/8−7 055.7h1/16+20 987.7h1/32+37 312.2h1/64+46 075.9h1/128。对于每一种材料，在保证最大压入载荷相同的情况下实验重复进行5次，图7～9所示分别为上述3种材料的载荷—位移曲线。根据载荷—位移曲线，同时应用该方法，可以确定上述3种被测试材料的弹性模量，结果如表3～5所示。从表2可以看出，对3种材料应用本方法获得的弹性模量测试结果均值与其已知值的相对误差均小于±6.0%，这也表明该方法是可行和非常有效的。此外，利用式(16)和(17)以及We/Wt和被测材料弹性模量Ε的均值可以估计应用本文作者所提方法测试上述 3种材料弹性模量的最大理论相对误差± δ+=±δ-分别为±13.8%、±8.8%和±2.1%，显然实际测试结果的相对误差−6.0%、5.5%和2.1%，均在上述最大误差范围内。

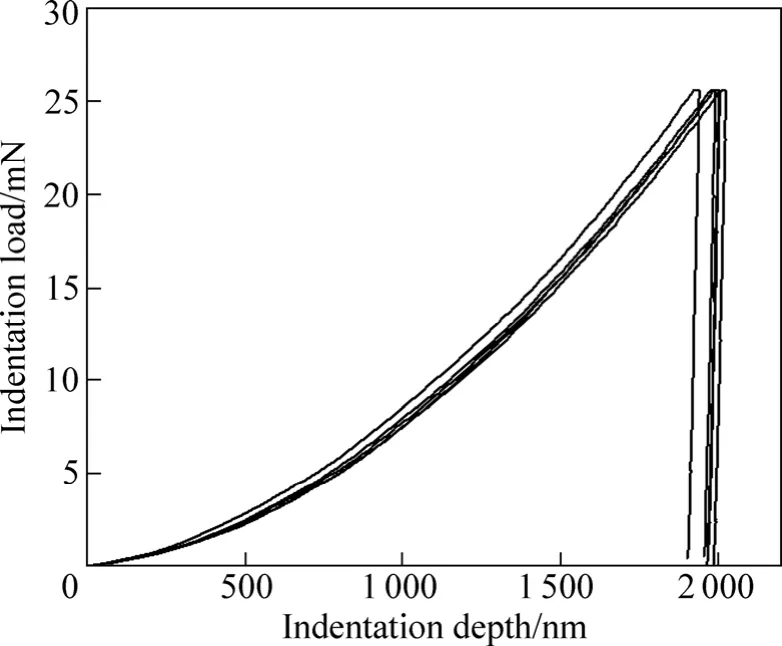
图7 铝单晶5次实验所得的载荷—位移曲线(Fm=25.5 mN)Fig.7 Load—displacement curves of five repetitive tests made on aluminum single crystal

图8 5次实验所得滚动轴承钢 GCr15的载荷—位移曲线(Fm=660 mN)Fig.8 Load—displacement curves of five repetitive tests made on GCr15 bearing steel

图9 熔融硅5次实验所得的载荷—位移曲线(Fm=460 mN)Fig.9 Load—displacement curves of five repetitive tests made on fused silica

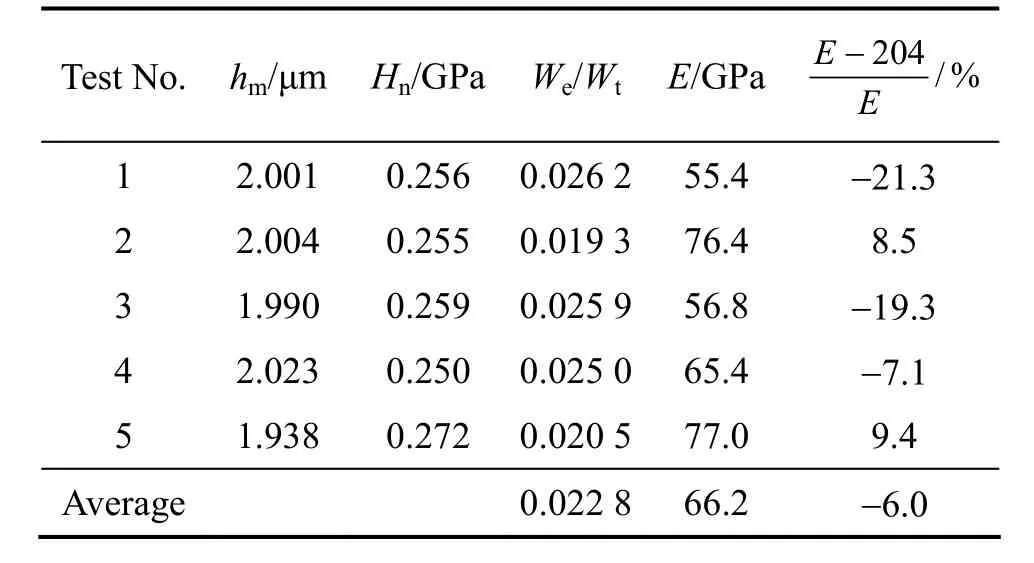
表3 仪器化压入法测试铝单晶的弹性模量结果Table 3 Elastic modulus of aluminum single crystal by instrumented indentation test

表4 仪器化压入法测试弹性模量的滚动轴承钢 GCr15结果Table 4 Elastic modulus of GCr15 bearing steel by instrumented indentation test

表5 仪器化压入法测试弹性模量的熔融硅结果Table 5 Elastic modulus of fused silica by instrumented indentation test

5 结论

1) 应用量纲定理和有限元方法对锥半角为 70.3°的金刚石圆锥压头压入弹塑性材料的压入响应进行了系统分析，通过引入联合弹性模量 Εc≡1/[(1−ν2)/Ε+1.32(1−νi2)/Εi] 来代替在弹性接触问题分析中广泛使用的压头及被压材料的折合弹性模量Εr≡1/[(1−ν2)/Ε+(1−νi2)/Εi]，揭示了在名义硬度 Hn和联合弹性模量Εc的比值与卸载功We和压入总功Wt的比值间存在的近似函数关系，即 Hn/Εc=f(We/Wt)=

2) 基 于 函 数 关 系 Hn/Εc=f(We/Wt)=，提出了由名义硬度Hn和压入We/Wt确定材料弹性模量的新方法，并且分析该方法的测试精度。

3) 通过对铝合金 6061−T6511 和 7075−T651、铝单晶、滚动轴承钢GCr15和熔融硅5种材料仪器化微米压入实验数据的分析表明，利用仪器化微米压入测试材料弹性模量的新方法是可行和非常有效的。

REFERENCES

[1] PETHICA J B, HUTCHINGS R, Oliver W C. Hardness measurement at penetration depth as small as 20 nm[J]. Phil Mag A, 1983, 48(4): 593−606.

[2] LOUBET J L, GEORGES J M, MARCHESINI O, MEILLE G.Vickers indentation curves of magnesium oxide (MgO)[J]. J Tribology, 1984, 106(1): 43−48.

[3] NEWEY D, WILKENS M A, POLLOCK H M. An ultra-low-load penetration hardness tester[J]. J Phys E: Sci Instrum, 1982, 15(1): 119−122.

[4] LAN H, VENKATESH T A. Determination of the elastic and plastic properties of materials through instrumented indentation with reduced sensitivity[J]. Acta Mater, 2007, 55(6): 2025−2041.[5] WEI P J, LIN J F. Modified method for continuous stiffness measurement[J]. J Mater Res, 2009, 24(3): 599−606.

[6] HERBERT E G, OLIVER W C, LUMSDAINE A, PHARR G M.Measuring the constitutive behavior of viscoelastic solids in the time and frequency domain using flat punch nanoindentation[J].J Mater Res, 2009, 24(3): 626−637.

[7] PHARR G M, STRADER J H, OLIVER W C. Critical issues in making small-depth mechanical property measurements by nanoindentation with continuous stiffness measurement[J]. J Mater Res, 2009, 24(3): 653−666.

[8] HAY J. Measuring substrate-independent modulus of dielectric films by instrumented indentation[J]. J Mater Res, 2009, 24(3):667−677.

[9] RANDALL N X, VANDAMME M, ULM F J. Nanoindentation analysis as a two-dimensional tool for mapping the mechanical properties of complex surfaces[J]. J Mater Res, 2009, 24(3):679−690.

[10] FENG G, QU S, HUANG Y, NIX W D. A quantitative analysis for the stress field around an elastoplastic indentation/contact[J].J Mater Res, 2009, 24(3): 704−718.

[11] LI Y P, ZHU X F, TAN J, WU B, WANG W, ZHANG G P.Comparative investigation of strength and plastic instability in Cu/Au and Cu/Cr multilayers by indentation[J]. J Mater Res,2009, 24(3): 728−735.

[12] QIN J, HUANG Y, XIAO J, HWANG K C. The equivalence of axisymmetric indentation model for three-dimensional indentation hardness[J]. J Mater Res, 2009, 24(3): 776−783.

[13] LIU L, OGASAWARA N, CHIBA N, CHEN X. Can indentation technique measure unique elatoplastic properties?[J]. J Mater Res, 2009, 24(3): 784−800.

[14] WEI Z, ZHANG G, CHEN H, LUO J, LIU R, GUO S. A simple method for evaluating elastic modulus of thin films by nanoindentation[J]. J Mater Res, 2009, 24(3): 801−815.

[15] NOHAVA J, RANDALL N X, CONTE N. Novel ultra nanoindentation method with extremely low thermal drift:Principle and experimental results[J]. J Mater Res, 2009, 24(3):873−882.

[16] PULECIO S A R, FARIAS M C M, SOUZA R M. Analysis of the tip roundness effects on the micro-and macroindentation response of elastic-plastic materials[J]. J Mater Res, 2009, 24(3):1037−1044.

[17] OLIVER W C, PHARR G M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments[J]. J Mater Res,1992, 7(6): 1564−1583.

[18] OLIVER WC, PHARR GM. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology[J]. J Mater Res,2004, 19(1): 3−20.

[19] PHARR G M, OLIVER W C, BROTZEN F R. On the generality of the relationship among contact stiffness, contact area, and elastic modulus during indentation[J]. J Mater Res, 1992, 7(3):613−617.

[20] DAO M, CHOLLACOOP N, VAN VLIET K J, VENKATESH T A, SURESH S. Computational modeling of the forward and reverse problems in instrumented sharp indentation[J]. Acta Materialia, 2001, 49(19): 3899−3918.

[21] PELLETIER H, KRIER J, CORNET A, MILLE P. Limits of using bilinear stress-strain curve for finite element modeling of nanoindentation response on bulk materials[J]. Thin Solid Films,2000, 379(1): 147−155.

[22] JOHNSON K L. Contact mechanics[M]. Cambridge, UK:Cambridge University Press, 1985: 85−105.

[23] ABAQUS: Version 6.2 (Hibbitt, Karlsson & Sorensen, Inc.,Pawtucket, RI, 2001)

Method for determining elastic modulus by instrumented indentation test

MA De-jun
(Department of Mechanical Engineering, The Academy of Armored Forces Engineering, Beijing 100072, China)

The instrumented indentation tests were analyzed by employing dimensional theorem and finite element method. A combined elastic modulus, Εc, was introduced to accurately reflect the combined elastic effect of an indenter and an indented material. Consequently, an approximate relationship between the ratio of nominal hardness to the combined elastic modulus and the ratio of unloading work to total work in indentation was revealed. Based on the relationship, a new method was then proposed for determining elastic modulus of materials, and its accuracy was analyzed. The effectiveness of the method was examined by several experimental examples.

elastic modulus; instrumented indentation; hardness; indentation work; finite element method

TG113.25；O242.21

A

1004-0609(2010)12-2336-08

国家自然科学基金资助项目(10672185)

2009-12-17；

2010-03-23

马德军，教授，博士；电话：010-66719289；E-mail：dejunma@yahoo.com

(编辑 龙怀中)