涉及到四个自映象的一个新的公共不动点定理
张军贺,陆 竞,谷 峰
(杭州师范大学 理学院,浙江 杭州 310036)
1 预备知识
张石生[1]教授和谷峰[2-3]教授在度量空间中自映象对可交换和相容的条件下,分别研究了涉及到3个自映象和4个自映象的φ-扩张型映象的公共不动点问题,之后,文献[3-6]研究了涉及到4个自映象的一些压缩型映象的公共不动点问题.该文利用映象对相容[7]和次相容[8]的条件,讨论了完备度量空间中涉及到4个自映象的一类新的φ-压缩型映象的公共不动点问题,获得了一个新的公共不动点定理.
定义1集合X上的自映象对(f,g)称为是可交换的,如果∀x∈X,有fgx=gfx.
定义2[7]度量空间(X,d)上的自映象对(f,g)称为是相容的,如果∀{xn}⊂X,当fxn→x,gxn→x,x∈X时,有d(fgxn,gfxn)→0(n→∞).
定义3[8]集合X上的自映象对(f,g)称为是次相容的,如果
{t∈X:f(t)=g(t)}⊂{t∈X:fg(t)=gf(t)}.
注1由定义易知,可交换映象对必是相容映象对,而相容映象对也必是次相容映象对,但反之不真.
定义4称函数φ满足条件(φ),如果函数φ满足条件(φ):φ:[0,∞)→[0,∞)是对t不减的和右连续的,且φ(t)
引理1设函数φ满足条件(φ),则有
(i)对任一实数t∈[0,∞),如果t≤φ(t),则t=0;

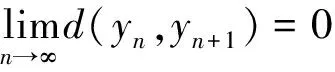
i)mi>ni+1,ni→∞(i→∞);
ii)d(ymi,yni)≥ε0;d(ymi-1,yni)<ε0,i=1,2,3,….
2 主要结果
定理1设S,T,A,B是完备度量空间X上的4个自映象,且满足以下条件:
i)SX⊂BX,TX⊂AX;
ii) 对于一切使得M(x,y)>0的x,y∈X,有下面的不等式成立:
d(Sx,Ty)≤φ(M(x,y)).
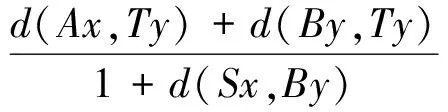
如果以下条件之一被满足,则S,T,A,B在X中有唯一公共不动点.
1)S,A之一连续,且(S,A)相容,(T,B)次相容;
2)T,B之一连续,且(S,A)次相容,(T,B)相容;
3)A,B之一为满射,且(S,A)和(T,B)都次相容.
证明任取x0∈X,因SX⊂BX,TX⊂AX,故存在X中的序列{xn},{yn}使得
y2n=Sx2n=Bx2n+1,y2n+1=Tx2n+1=Ax2n+2,n=0,1,2,….
令dn=d(yn,yn+1),证
(1)
由条件ii)得
d(y2n,y2n+1)=d(Sx2n,Tx2n+1)≤
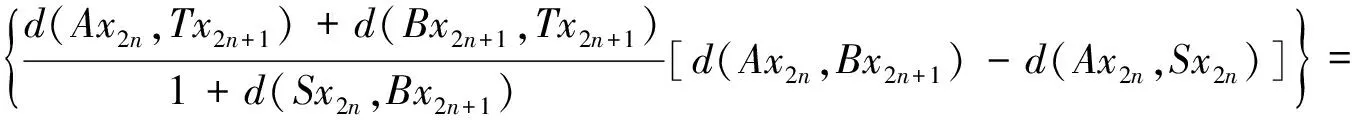
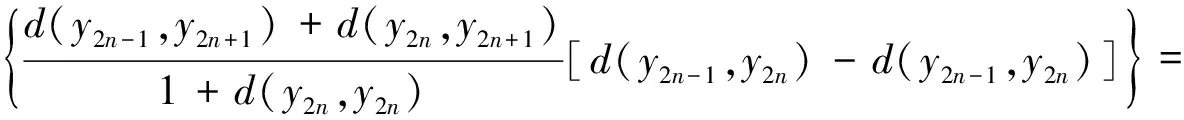
φ(0)≤φ(d(y2n-1,y2n))(因φ(t)对t不减).
(2)

下证{yn}是X中的Cauchy列.否则,由引理2知,必存在某一ε0>0和正整数列{mi},{ni},使得
a)mi>ni+1,ni→∞(i→∞);
b)d(ymi,yni)≥ε0;d(ymi-1,yni)<ε0,i=1,2,3,….
令ei=d(ymi,yni),则有
ε0≤ei=d(ymi,yni)≤d(ymi,ymi-1)+d(ymi-1,yni)<ε0+d(ymi-1,ymi),
注意到式(1),于上式令i→∞得
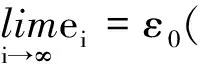
(3)
另一方面,因为
ei=d(ymi,yni)≤d(ymi,ymi+1)+d(ymi+1,yni+1)+d(yni+1,yni),
(4)
对上式右端第二项分4种情况讨论如下:
Ⅰ) 当mi为偶,ni为奇时,由条件ii)得
d(ymi+1,yni+1)=d(Txmi+1,Sxni+1)=d(Sxni+1,Txmi+1)≤

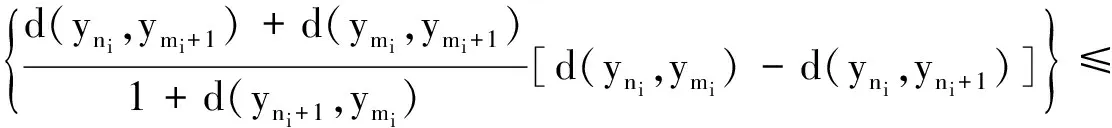
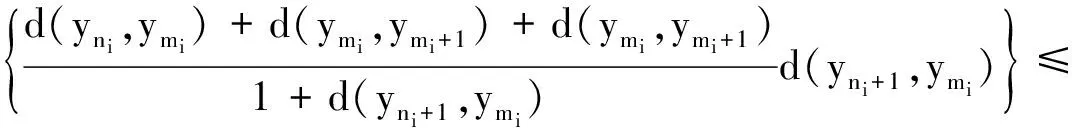

注意到式(3)和φ(t)的右连续性,令i→∞对上式取极限得

(5)
利用式(1)和(5),在式(4)中令i→∞得ε0≤ei≤0+φ(ε0)+0,即ε0≤φ(ε0),由引理1(i)知ε0=0,此与ε0>0矛盾.
Ⅱ) 当mi,ni均为偶数时,首先有
d(ymi+1,yni+1)=d(Txmi+1,Txni+1)≤d(Sxni,Txmi+1)+d(Sxni,Txni+1),
(6)
再由条件ii)得
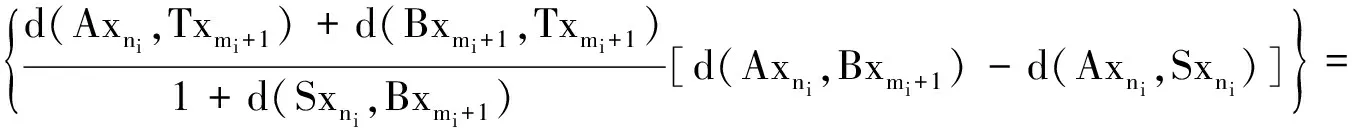
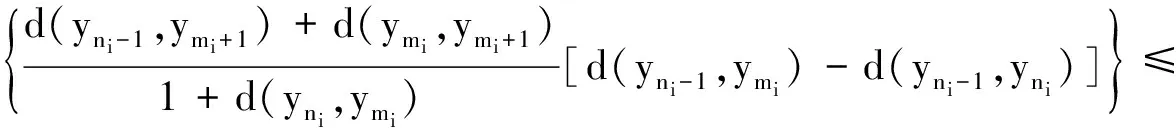


于上式中令i→∞取极限得
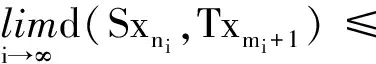
(7)

同理可证当mi,ni同为奇数;mi为奇数,ni为偶数时也可引出同样的矛盾.这些矛盾说明{yn}是X中的Cauchy列,由X完备.设yn→y*∈X,则{y2n-1}和{y2n}也都收敛于y*,即
Ax2n=y2n-1→y*,Sx2n=y2n→y*(n→∞).
(8)
1) 设S,A之一连续,且(S,A)相容,(T,B)次相容.
如果A连续,则{A2x2n}与{ASx2n}都收敛于Ay*,由式(8)和(S,A)相容得d(SAx2n,ASx2n)→0,因此SAx2n→Ay*(n→∞).由条件ii)得
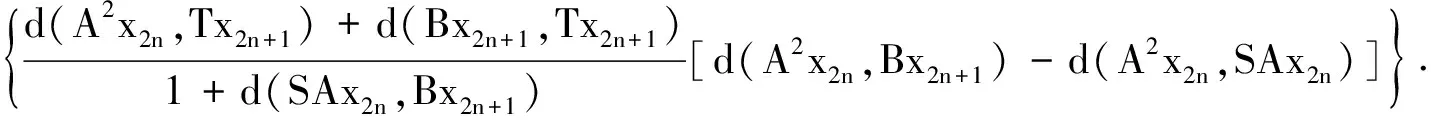
于上式中令n→∞得

由引理1(i)知d(Ay*,y*)=0,进而可得
Ay*=y*.
(9)
由条件ii)得

于上式中令n→∞并利用式(9)得

由引理1(i)知d(Sy*,y*)=0,进而可得
Sy*=y*.
(10)
由SX⊂BX知,存在u∈X使得
y*=Ay*=Sy*=Bu.
(11)
由条件ii)及式(11)得
d(Bu,Tu)=d(Sy*,Tu)≤
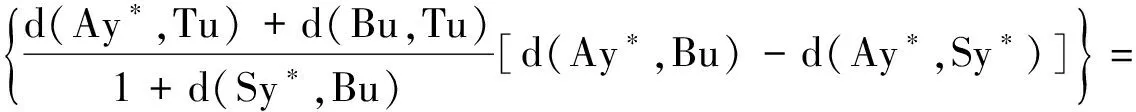
由引理1(i)知d(Bu,Tu)=0,进而可得
Bu=Tu,
(12)
由式(12)及(T,B)的次相容性可得
Ty*=TBu=BTu=By*.
(13)
下证Ty*=y*.事实上,由条件ii)及式(13)可得
d(y*,Ty*)=d(Sy*,Ty*)≤
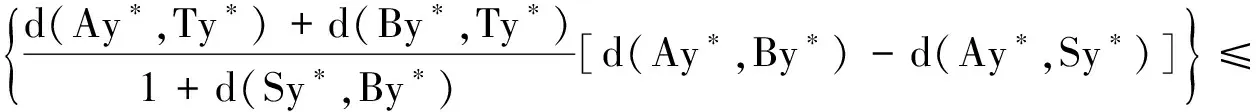
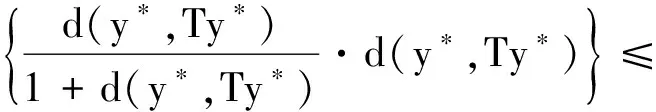
由引理1(i)知d(y*,Ty*)=0,进而可得Ty*=y*,因此可得y*=Ay*=Sy*=By*=Ty*,即y*是S,T,A,B的公共不动点.
如果S连续,类似上述证明可得y*=Ay*=Sy*=By*=Ty*,即y*是S,T,A,B的公共不动点.
下证公共不动点的唯一性.设z也是S,T,A,B的一个公共不动点,由条件ii)得


由引理1(i)知d(y*,z)=0,进而可得y*=z.所以y*是S,T,A,B的唯一公共不动点.
2) 当T,B之一连续,且(S,A)次相容,(T,B)相容,类似1)可证.
3) 设A,B之一为满射,且(S,A)和(T,B)都是次相容.
如果A是满射,则对y*∈X,存在u∈X使得Au=y*.利用条件ii)得
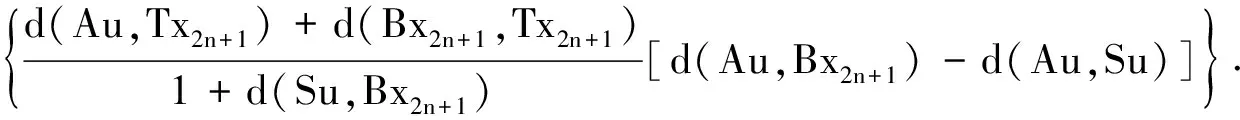
(14)
在式(14)中令n→∞得

由引理1(i)知d(Su,y*)=0,进而可得Su=y*,所以Au=Su=y*.于是,由(S,A)的次相容性可知,有Ay*=ASu=SAu=Sy*.在式(14)中由y*代替u同理可得Sy*=y*,于是Ay*=Sy*=y*.之后与1)的证明类似,可证y*是S,T,A,B的唯一公共不动点.
当是满射时同理可证y*是S,T,A,B的唯一公共不动点.
注2本定理的压缩条件ii)是新的;
注3即使定理1中分别取1)S=T;2)A=B;3)S=T且A=B;4)S=T且A=B=I(I是表示恒等映象),这几种特殊情况所对应的结果也是新的.
定理2设(X,d)是完备度量空间,A,B,{Ti}i∈I(I是指标集,I的势不小于2)分别是X上的自映象和自映象族,若A,B,{Ti}i∈I满足以下条件:
i)TiX⊂BX,TiX⊂AX,∀i∈I;
ii) 对于∀i,j∈I(i≠j)和一切使得Mij(x,y)>0的x,y∈X,有下面的不等式成立:
d(Tix,Tjy)≤φ(Mij(x,y)),
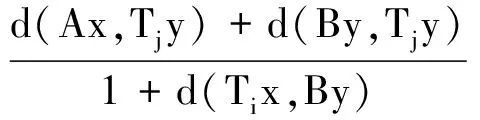
如果以下条件之一被满足,则A,B,{Ti}i∈I在X有唯一的公共不动点.
1)Ti(∀i∈I),A之一连续,且(Ti,A)相容,(Ti,B)次相容;
2)Ti(∀i∈I),B之一连续,且(Ti,A)次相容,(Ti,B)相容;
3)A,B之一为满射,且(Ti,A)和(Ti,B)都是次相容.
证明对∀i,j,m∈I,i≠j,i≠m,由定理1知A,B,Ti,Tj和A,B,Ti,Tm分别存在唯一的公共不动点xij和xim.下面证明xij=xim.利用条件ii)有
d(xij,xim)=d(Tixij,Tmxim)≤
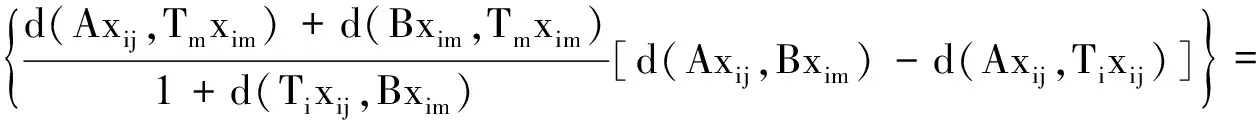
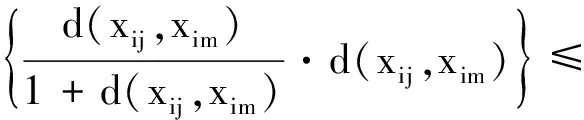
由引理1(i)知d(xij,xim)=0,即xij=xim,由i,j,m的任意性可知,A,B,{Ti}i∈I在X有唯一的公共不动点.
[1] 张石生.不动点理论及其应用[M].重庆:重庆出版社,1984:1-99.
[2] 谷峰.关于φ扩张相容映像的公共不动点定理[J].宝鸡文理学院学报:自然科学版,2001,21(3):171-179.
[3] 谷峰,高伟,田巍.不动点定理及非线性算子的迭代收敛性[M].哈尔滨:哈尔滨科学技术出版社,2002:17-119.
[4] 何振华,谷峰.两对非相容映象的一个新的公共不动点定理[J].宝鸡文理学院学报:自然科学版,2006,26(1):7-9.
[5] 陈军民,谷峰.一类新的φ-压缩映象的公共不动点定理[J].杭州师范学院学报:自然科学版,2007,6(6):414-418.
[6] 傅秋平.一类新的φ-压缩映像的公共不动点定理[J].高师理科学刊,2006,26(4):1-5.
[7] Jungck G. Compatible mappings and common fixed points[J]. Internat J Math & Math Sci,1986,9(4):771-779.
[8] 刘立山.(次)相容映象的公共不动点定理与广义Ishikawa迭代逼近定理[J].曲阜师范大学学报:自然科学版,1990,16(2):40-44.

