双荷粒子系统偶极子电磁辐射场的双矢势对偶理论

买买提阿布都拉·艾克木,沙依甫加马力·达吾来提，买买提明·艾尼瓦尔,买买提吐尔孙·牙库甫

(1．和田师范专科学校 物理系，新疆 和田 848000；2．新疆大学 物理科学与技术学院，新疆 乌鲁木齐 830046)

在现行教材及文献中，“偶极子辐射”内容是天线辐射、发光机制的基础理论，因此对偶极子辐射的研究具有十分重要的意义.在无磁荷存在的情况下，对于电磁辐射特别是偶极子辐射的研究，已有相当完备的理论和方法，但在有磁荷存在的情况下电磁辐射问题有待于进一步的深入研究和讨论.在有源情况下，Maxwell方程是没有对偶性的，为了在有源情况下保持Maxwell方程的电磁对偶性，P.Dirac提出了磁荷(或磁单极)存在的可能性，并指出磁单极的存在是电荷量子化的来源[1]278-280.电荷与磁荷不同的是，电荷在其周围产生的电场和电势是连续的，而磁荷在其周围产生的磁场的磁矢势是沿一定的线发散的，这条线就是Dirac弦.由于磁荷在实验中没有找到，所以过去半个多世纪关于磁荷及电磁对偶性的研究进展很缓慢.近年来在超对称性和非Abel规范理论的研究中，磁单极引起了人们极大的兴趣和关注.当然，Dirac弦就是非物理意义的奇异弦，因为通常情况下物理上有意义的场不应该有奇异部分.文献[2-3]从电磁对偶性的观点出发首次引入双矢势的概念，提出了电磁场双矢势的描述形式，并证明了可以避开奇异弦而得到电荷量子化条件.在此基础上，笔者对双荷粒子系统偶极子电磁辐射场的特性进行了讨论.

1 广义Maxwell方程和广义d’Alambert方程

真空中有磁荷存在时的Maxwell方程可表示如下[2]:

(1)

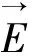
磁荷存在时可引入双矢势,即

(2)

(3)

取如下洛仑兹规范[1]431-438:

(4)

则存在磁荷时的Maxwell方程可表述成为[4]:

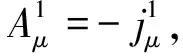
(5)

利用(1)，(3)两式，并利用磁荷与电荷同时存在时的洛仑兹规范，经过一定的推导，可以得到在双矢势下有磁荷存在时的d’Alambert方程[4]：

(6)

此方程组称为广义d’Alembert方程组.这一方程具有电磁对偶性，可参照经典电动力学中无磁荷的情况，用推迟势的方法来求解.

2 双荷粒子系统的电磁辐射场强度

由方程(6)可见，电荷产生电场标量势波动，电流产生磁场矢量势波动，磁荷产生磁场标量势波动，磁流产生电场矢量势波动.设以纯电荷与纯磁荷分别描写双荷粒子的不同方面，在运动状态下

(7)

双荷粒子系统的广义d’Alambert方程原则上可以用推迟势的方法来求解.参照经典电动力学的方法，可以得到广义d’Alembert方程(6)在式(7)给出的条件下的推迟势解[4]:

(8)

(9)

这就是有磁荷存在时在双矢势下场源在空间辐射的电场和磁场.它是由纯电荷q和纯磁荷g共同组成的双荷粒子系统的场强.显然，此式具有对偶对称性.

3 双荷粒子系统偶极辐射场的特性

现在用式(8)的推迟解来讨论作简谐振荡的双荷粒子系统偶极子电磁辐射场问题.

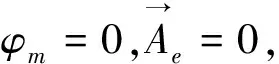
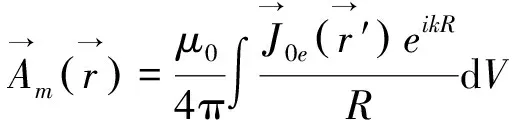
(10)

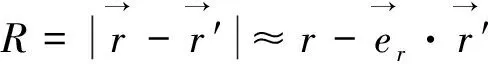
(11)

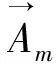
(12a)

上式也可以写为

(12b)

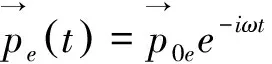
(13)

其辐射平均能流密度为

(14a)

上式也可以写为

(14b)

式中，θ为偶极矩与辐射传播方向之间的夹角.

辐射角分布为

(15a)

上式也可以写为

(15b)

辐射功率为

(16a)

上式也可以写为

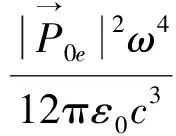
(16b)

可见，辐射能流密度、角分布和功率都是正比于频率的四次方.因此当频率变高时，辐射功率迅速增大.

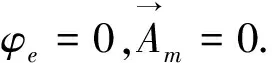
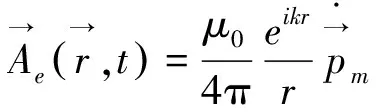
(17a)

上式也可以写为

(17b)

(18)

其辐射平均能流密度为

(19a)

上式也可以写为

(19b)

式中，θ为偶极矩与辐射传播方向之间的夹角.

辐射角分布为

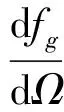
(20a)

上式也可以写为

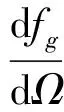
(20b)

辐射功率为

(21a)

上式也可以写为

(21b)

由此也可以看出，辐射能流密度、角分布和功率都是正比于频率的四次方.

3) 双荷粒子系统偶极辐射场.双荷粒子是由电荷和磁荷所组成的一个统一的广义的粒子,因此，它在空间中任意处激发的场是由纯电荷激发场和纯磁荷激发场叠加而成的.其总辐射场强为

(22)

总辐射平均能流密度为

(23a)

上式也可以写为

(23b)

总辐射角分布为

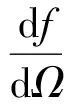
(24a)

上式也可以写为

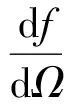
(24b)

总辐射功率为

(25a)

上式也可以写为

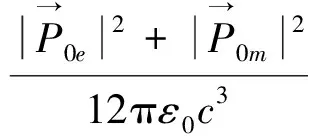
(25b)

此处要特别强调的是，在引入双矢势后，单频振荡的磁偶极矩和磁偶极辐射与经典电动力学的磁偶极矩和磁偶极辐射含义及结果是不一样的.

4 结 论

该文在引入双荷粒子和双矢势描述法的基础上，着重讨论电磁场辐射问题.首先回顾和分析了引入磁单极的重要性和必要性，给出了双矢势的表达式及具有电磁对偶性的广义Maxwell方程.其次讨论了在有磁荷存在的情况下引入双矢势后的广义d’Alambert方程及其推迟势解.最后在推迟势多极展开式中选取电偶极和磁偶极辐射有关的推迟势项，计算出了辐射场及其特征量.值得指出，在得到场强表达式的过程中，没有使用Dirac弦的概念，因此避免了物理上的奇异问题；在无磁荷(g=0)情况下，推导出的结论与经典电动力学中得到的电磁辐射的表达式完全一样.

[1] Jackson J.经典电动力学:上册[M].朱培豫,译.北京:人民教育出版社，1978.

[2] Li Kang, Naon C M. An alternative formulation of classical electromagnetic duality[J]. Modern Physics Letter A,2001,16(26):1671-1683.

[3] 陈文俊，李康.电磁对偶的经典电动力学与电荷量子化[J].浙江大学学报:理学版，2001,28(6):626-629.

[4] 王剑华，李康.低速Dyon粒子电磁辐射的双矢势对偶理论[J].浙江大学学报:理学版，2003,30(3):271-273.

[5] 上海物理学会教学研究委员会.理论物理习题集[M].上海:上海科学技术文献出版社，1982:200-207.

[6] 俞允强.电动力学简明教程[M].北京:北京大学出版社，2003:120-129.

[7] 郭硕鸿.电动力学[M].2版.北京:高等教育出版社，2001:193-200.