基于串行计算的排序算法实证分析

陈根方，张立印

(杭州师范大学 信息科学与工程学院,浙江 杭州 310036)

(T1)p-1-(T2)p-1≥0

(T1)p+1-(T2)p+1≤0

0 前 言

排序算法是最常见的计算机算法之一，在大型计算机中，排序占用了CPU大约25%的运行时间.排序的对象是有限集合或无序序列中的元素，排序是按某种规则将其重新进行排列，最常用的规则是元素某个关键字的大小关系，排序后的序列元素之间的前后位置关系符合这种规则.

用来解决排序问题的算法多达几十种，如表1所示为常见的排序算法[1].常用的衡量排序算法优劣的因素是：时间复杂度、空间复杂度、稳定性和适合场合.其中最主要的衡量因素是时间复杂度，常见的简单排序算法有插入排序、冒泡排序、选择排序[2]等，它们的平均时间复杂度都是O(n2)；而时间复杂度是O(nlogn)的常见排序算法有堆排序、合并排序和快速排序[2]；这6种排序算法都是基于比较的排序算法，也就是说在排序过程中，需要进行大量的关键字值之间的大小比较，其中平均时间稳定性较好的排序算法是快速排序算法.还有一些时间复杂度是O(n)的排序算法也被逐步发现，比如计数排序[3]、基数排序[4]、桶排序[5]、Flash sort[6],分段快速排序[7]、二次分“档”链接排序方法[8]等等.

表1 常见的排序算法

不同的算法适用于不同的场合，有的算法适用于在外存中排序，如合并排序算法；有的算法适用于内存中排序，如快速排序算法；有的适用于并行计算，有的适用于串行计算，有的适用于时空交换技术，有的适用于大容量的数据，有的适用于小容量的数据.

快速排序算法是著名计算机算法大师Tone Hoare在1960年发表的，是目前为止基于关键字比较的排序算法中平均性能最佳的排序算法，它的平均时间复杂度是O(nlogn)，最坏情况下的时间复杂度是O(n2).

1 相异密度因子

地址映射计数排序算法是非比较排序算法的典型例子，它的基本思想是：

假设待排序的元素个数是n个，记为A[n]，并且这些元素都是正整数，其中最小的元素是1，最大的元素为m.则算法过程是：1)申请能存放m个正整数的空间，Temp[m];2)初始化,使得Temp[i]=0，i=1～m;3)对所有的i=1～n, 进行Temp[A[i]]=Temp[A[i]]+1;4)定义变量sum=1;5)i从1变化到m,如果Temp[i]≠0，那么j从sum变化到sum+Temp[i]-1，使得每个A[j]=i，然后，sum=sum+Temp[i].

很显然，时间复杂度T(n)为上述5个步骤的CPU时间之和.

T(n)=O(1)+O(m)+O(n)+O(1)+O(m)=O(m)+O(n)

(1)

由于n个元素分布在1～m之间，而且这n个元素中可能存在相同的元素，假设这n个元素中互不相同的相异元素个数是k个，显然有，1≤k≤n，且k≤m.

(2)

和快速排序算法比较起来，对于情况1)，显然快速排序算法比地址映射计数排序算法要慢；对于情况2)，考虑两种算法所用CPU时间相同的特殊情况，这时有：

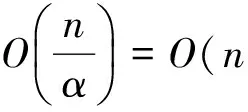
(3)

2 实验结果

显然，快速排序算法和地址映射计数排序算法两者即可以用串行计算方法实现，也可以用并行计算方法实现，这里采用串行计算方法实现和比较两个算法；同时，实现的过程全部在内存中进行，采用普通PC机作为实验对象，CPU为AMD AthlonTM64 X2 Dual Core Processor 5200+2.7 GHz,1.75 GB的内存，编程语言采用VC++6.0.

实验用的数据范围1～m，元素个数为n，其中，n=10～10000000,m=10～270000000，所有的元素值都是由VC++的随机函数产生.实验分为5个小的实验：

1)取m=n，n的范围为10～20000000，其中10～10000000独立运行了1次，而n=10000000和n=20000000，则分别运行了107次和119次(随机次数)，快速排序算法和地址映射计数排序算法的运行时间见表2，由表1可知，快速排序算法的运行时间比地址映射计数排序算法要长的多.

2)取m=n*log2n，n的范围为2p，(p=1～7)，运行次数是4次，计算出平均运行时间，见表3，由表2可知，快速排序算法的运行时间和地址映射计数排序算法有所接近.

表2 当n=m时，两种算法的平均运行时间和运行次数

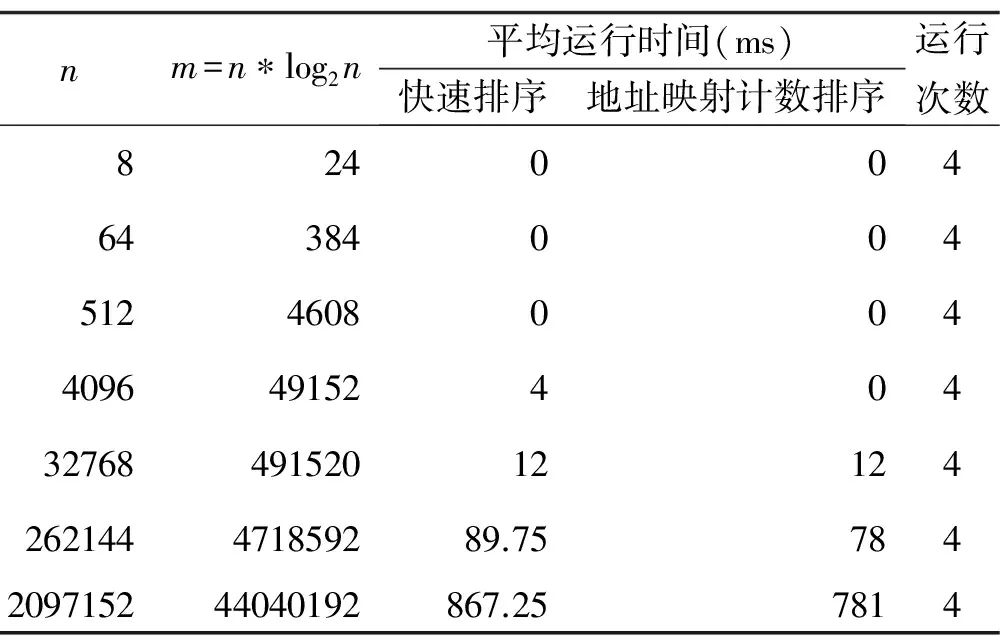
表3 当m=n*log2n时，两种算法的平均运行时间和运行次数

3)取n=1000000，m=n*p，(p=1～29)，α=1/p，Y轴是两种算法运行12次的总运行时间，X轴是p的递增值.运行结果见图2，基本水平的线是快速排序算法的运行时间，而基本保持一定斜率的线是地址映射计数排序算法的运行时间，它们在p=21的时候相交.

图1 当n=1000000,m=n/α,两种算法重复运行12次的结果

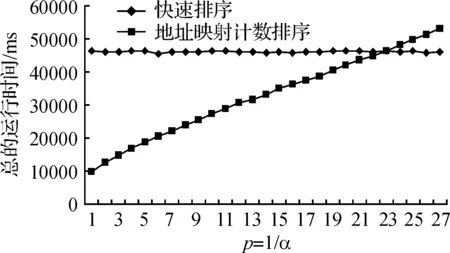
图2 当n=10000000,m=n/α,两种算法重复运行10次的结果

4)取n=10000000，m=n*p，(p=1～27)，α=1/p，Y轴是两种算法运行10次的总运行时间，X轴是p的递增值.运行结果见图3，基本水平的线是快速排序算法的运行时间，而基本保持一定斜率的线是地址映射计数排序算法的运行时间，它们在p=23的时候相交.

5)取n=1000000*q，(q=1～10)，对于每个n，取m=n*p，(p=1～27)，α=1/p.对于每个n，存在一个p，记为p′，使得快速排序算法的运行时间(T1)p和地址映射计数排序算法的运行时间(T2)p的差满足4个条件：

|(T1)p′-(T2)p′|≤|(T1)p-1-(T2)p-1|

(4)

|(T1)p′-(T2)p′|≤|(T1)p+1-(T2)p+1|

(5)

(T1)p-1-(T2)p-1≥0

(6)

(T1)p+1-(T2)p+1≤0

(7)

和p′相应的α记为α′.

通过观察实验，得到了不同n能满足(4)-(7)的p′，见表4，可以发现，相异密度因子α和1/log2n，比较接近.

通过实验，验证了式(3)是成立的.

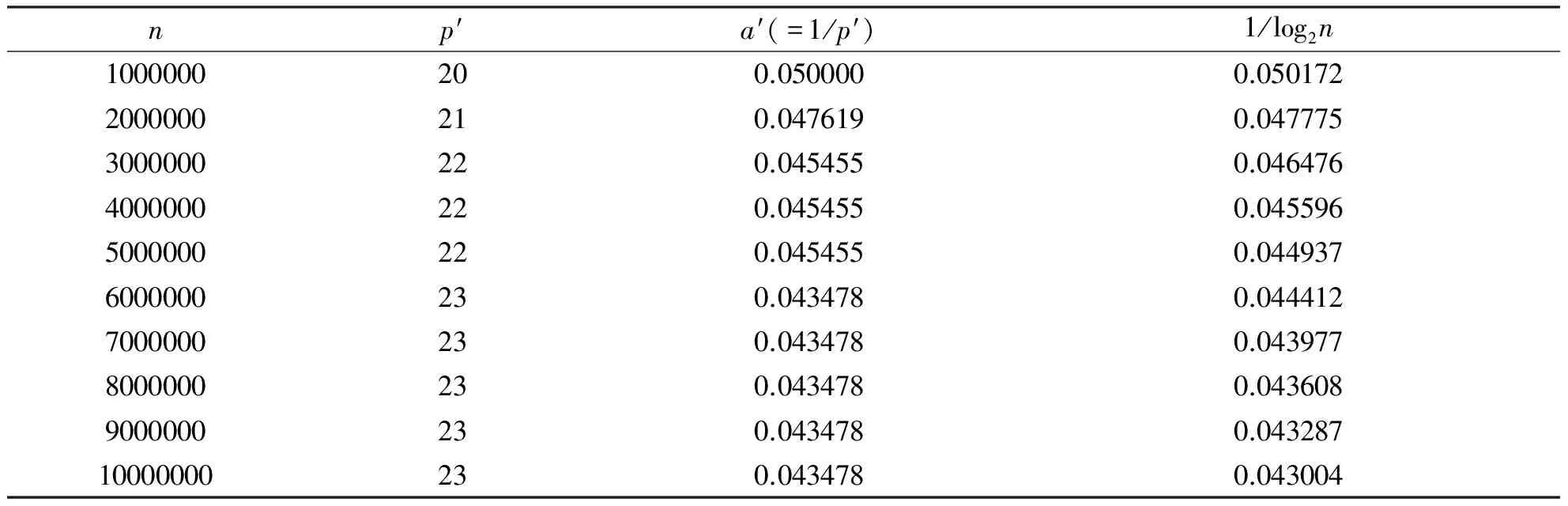
表4 当两种算法运行时间的绝对值差最小时，α的值和1/log2n的比较表

3 结 论

快速排序算法是最出色的排序算法之一，广泛应用于计算机的各个应用领域，而当元素的个数n和元素的关键字大小范围m的比例α满足：α>log2n时，它比地址映射计数排序算法的运行时间长，因此，如果待排序的数据满足α>log2n时，可采用地址映射计数排序算法，反之可采用经典的快速排序算法.

随着计算机技术飞速发展，新的排序算法不断发现，如纵横多路并行归并算法[9]、基于编号的选择算法[10]、基于完全K叉树的适应性堆排序算法[11]等等，探索面向不同应用领域排序算法是新的研究方向.

[1] 维基百科.排序算法[EB/OL].(2008-08-01)[2010-01-11].http://zh.wikipedia.org/zh-cn/排序算法.

[2] 严蔚敏，吴伟民.数据结构(C语言)[M].北京:清华大学出版社,1997:264-285.

[3] Sedgewick R. Algorithms in C++[M]. MA USA: Addison Wesley Publishing Company,1998:191-193.

[4] Aho, Hopcroft, Ullman. The Design and Analysis of Computer Algorithm[M]. MA USA: Addison Wesley Publishing Company,2003:76-100.

[5] 杨大顺，顾芸瑛.按字节桶分配链接排序法[J].计算机研究与发展,1996,33(2):132-139.

[6] Neubert Karl-Dietrich. The Flashsort Algorithm[J]. Dr. Dobb’s Journal,1998(2):123-129.

[7] 唐向阳.分段快速排序算法[J].软件学报,1993,4(2):53-57.

[8] 杨红颖，王向阳.任意分布数据的二次分“档”链接排序算法研究[J].小型微型计算机系统,2000,12(19):993-996.

[9] 王颖，李肯立，李浪,等.纵横多路并行归并算法[J].计算机研究与发展，2006，43(12)：2180-2185.

[10] 原民民，董建刚.一种改进的基于编号的选择排序方法[J].科学技术与工程，2009，9(1):139-142.

[11] 蒲保兴，陶世群.基于完全K叉树的适应性堆排序算法[J].山西大学学报:自然科学版,2008,31(2)：167-172.