对称空间中的重合点和公共不动点定理

李付成,谷 峰*

(1.杭州师范大学 应用数学研究所，浙江 杭州 310036;2.杭州师范大学 理学院，浙江 杭州 310036)

1 引言和预备知识

该文的主要目的，是在没有连续性的要求下，得到一些关于更一般的压缩条件下的重合点和公共不动点的定理.在压缩条件中给出了一个非度量函数d，其中d有如下性质：序列{xn}收敛到x当且仅当d(xn,x)→0.在此选择对称空间也就是半度量空间作为文章的基本空间.

下面给出一些定义.

定义1[2]集合X上的一个对称是一个非负实函数d:X×X→[0,∞)，满足∀x,y∈X，有

(i)d(x,y)=0⟺x=y;

(ii)d(x,y)=d(y,x).

如果d是集合X上的对称，那么对x∈U和ε>0，记B(x,ε)={y∈X:d(x,y)<ε}.X上的一个拓扑τ(d)定义为：U∈τ(d)当且仅当对每个x∈X,存在ε>0使得B(x,ε)⊂U.一个集合S⊂X是b∈X的一个邻域当且仅当存在U∈τ(d)使得b∈U⊂S.如果对每个x∈X和每个ε>0，B(x,ε)都是x在拓扑τ(d)中的一个邻域，则称对称d是一个半度量.

定义2[2]一个半度量空间X是一个拓扑空间，其拓扑τ(d)由X上的半度量d生成.在后面，对称空间亦即半度量空间将表示为(X,d).

对称和半度量之间的区别是明显的，因为很容易的构建一个对称d使得B(x,ε)不是x在τ(d)中的一个邻域.对于X上的一个对称d，下面的两个公理由Wilson[11]给出：

(W3)给定{xn}⊂X，x,y∈X，如果d(xn,x)→0且d(xn,y)→0，则x=y；

(W4)给定{xn},{yn}⊂X，x∈X，如果d(xn,x)→0且d(xn,yn)→0，则d(yn,x)→0.

易知，对于一个半度量d，如果τ(d)是Hausdorff的，则(W3)成立.

定义3[4]在对称(半度量)空间(X,d)中，一对自映像(f,g)被称为是相容的，如果

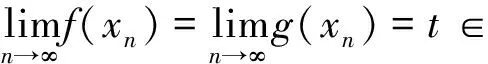
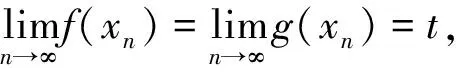
定义4[5]在对称(半度量)空间(X,d)中，自映像对(f,g)称为是弱相容的(或重合点可交换)，如果从fx=gx可推得fgx=gfx.

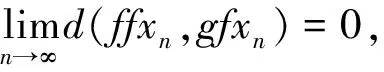
在文章中，引进一个新的(Ag)型弱相容映像的概念如下.

定义6在对称(半度量)空间(X,d)中，自映像对(f,g)称为是(Ag)型弱相容的，如果从fx=gx可推得ffx=gfx.

注1由定义可知(Ag)型相容映像一定是(Ag)型弱相容映像.反之不真，例子如下：

例1令(X,d)=([0,10],|·|)，定义f,g:[0,10]→[0,10]如下：

显然，f(x)=g(x)当且仅当x=0，且映像对是(Ag)型弱相容的，这是因为

ff(0)=f(0)=0,gf(0)=g(0)=0.

故映像对(f,g)不是(Ag)型相容映像.

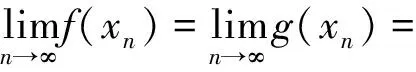
文章的目的是在对称(半度量)空间的框架中，证明了几个新的重合点和公共不动点定理，所得结果改进和推广了文献[1-3]中的相关结果，同时也给出了验证和说明该结果的实际例子.

2 主要结果

定理1设(X,d)是一个满足条件(W3)的对称(半度量)空间(τ(d)是Hausdorff拓扑).f和g是X上的自映像，且满足以下条件

(i)f和g满足性质(E-A)；

(ii)对于所有的x,y∈X,x≠y，有

(1)

其中1≤k<2,0≤α,β<1.如果f(X)是X的一个d-闭(τ(d)-闭)子集，则f和g有重合点.

证明首先，需要指出的是,半度量空间(X,d)中的序列{xn}关于拓扑τ(d)收敛到点x当且仅当d(xn,x)→0.为了证明它，假设xn→x(关于拓扑τ(d))，ε>0.因为B(x,ε)是x的一个邻域，则存在U∈τ(d)使得x∈U⊂B(x,ε).由假设xn→x，所以存在一个自然数m∈N，当n≥m时，有xn∈U⊂B(x,ε).故当n≥m时，有d(xn,x)<ε.即d(xn,x)→0.反之由τ(d)的定义显然可得.

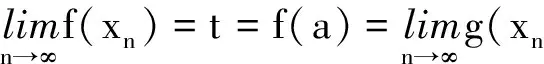
令n→∞且两边取极限，有

矛盾，故f(a)=g(a)，即a是f和g的一个重合点.定理1得证.

注2在定理1中，令α=β=0，则得文献[2]中的定理2.1.

下面是定理1的一个变形.

定理2如果定理1中f(X)的d-闭性(τ(d)-闭性)由g(X)的d-闭性(τ(d)-闭性)性所取替，且g(X)⊂f(X)，其它的条件不变，则定理1的结论仍然成立.

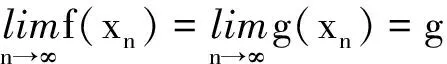
令n→∞，得

矛盾，故g(a)=g(b)=f(b)，这便证明了b是f和g的一个重合点.证毕.

注3在定理2中，令α=β=0，则得文献[2]中的定理2.2.

定理1和定理2保证了重合点而不是公共不动点的存在性，鉴于此，可将压缩条件(1)稍加修改，将得到公共不动点的存在性定理如下.

定理3在定理1和2的假设下，如果f和g是弱相容映像对，并且压缩条件(1)由下面的压缩条件所取代：对所有的x,y∈X,x≠y，有

(2)

其中1≤k<2，0≤α,β<1，则f和g有唯一的公共不动点.

证明由定理1和2知，f和g有一个重合点a，即f(a)=g(a).由于f和g是弱相容映像，从而fg(a)=gf(a)，进而有fg(a)=ff(a)=gg(a)=gf(a).现在证明gg(a)=g(a)，若不然，则根据式(2)可得

矛盾.因此ga=gga=fga=ffa=gfa，即ga是f和g的公共不动点.

下证f和g的公共不动点唯一.事实上，设t1和t2是f和g的公共不动点，即f(t1)=g(t1)=t1和f(t2)=g(t2)=t，且t1≠t2，则由压缩条件(2)可得

矛盾.故必有t1=t2，即f和g的公共不动点是唯一的.

注4在定理3中，令α=β=0，则得文献[2]中的定理2.3.

定理3也改进和推广了Aamri-Moutawakil[1]以及Pant-Pant[3]的相关结果.

定理4在定理1和2的假设下，如果f和g是(Ag)型弱相容映像对，并且压缩条件(1)由式(2)所代替，其中1≤k<2，0≤α,β<1，则f和g有唯一的公共不动点.

证明利用(Ag)型弱相容映像的定义，类似定理3的方法不难证明.略去.

注5定理4从两个方面改进了文[2]中定理2.3：

1)用(Ag)型弱相容的条件代替弱相容条件；

2)定理4的压缩条件中取α=β=0的特殊情况则为文[2]中定理2.3的条件.

下面给出一个例子，目的是说明假设的有效性和文章结果普遍性.以下例子给出了一个满足文章定理假设的非度量压缩条件.

例2令X=[0,1]，定义X上的对称d(x,y)=(x-y)2,∀x,y∈X.定义f,g:X→X如下：

显然f(X)={0}∪[1/3,2/3]在X上是d-闭的.由于序列{1/3-1/n}⊂[0,1]满足

所以映像对(f,g)满足性质(E-A).又f(x)=g(x)当且仅当x=1/3，而且

f(1/3)=g(1/3)=1/3⟹fg(1/3)=gf(1/3)=ff(1/3)=1/3，

因此映像对(f,g)是弱相容的，也是(Ag)型弱相容的.

通过常规的计算可以说明压缩条件(2)对每个x,y∈X,x≠y都成立.由于由d生成的拓扑定义在区间[0,1]上,它是Hausdorff空间并且自然满足条件W3，这样就满足了定理3和4的全部条件,1/3是f和g的唯一公共不动点.这里有一点需要说明的是d不是一个度量,因为d(0,1)=1>1/9+4/9=d(0,1/3)+d(1/3,1)，这样所有可用的度量公共不动点定理就不能应用到该例题中.注意到无论是f还是g在唯一的公共不动点1/3处都是不连续的.

这里可以观察到的是例2还满足定理1和定理2的条件,因为g(X)={1/3,1/2}⊂{0}∪[1/3,1/2]=f(X)及g(X)是d-封闭的.最后,还需要说明的是条件W3也是至关重要的,因为它确保了收敛序列极限的唯一性.不难找出一个可以导出非Hausdorff拓扑的对称度量，比如T1-拓扑,它允许一个序列收敛到不止一个极限点(例:X=R，d(x,y)=1/|x-y|,当x≠y且d(x,y)=0时，其中xn=n,n∈N).

[1] Aamri M, Moutawakil DI. Some new common fixed point theorems under strict con-tractive conditions[J]. J Math Anal Appl,2002,270:181-188.

[2] Imdad M, Javid Ali, Ladlay Khan. Coincidence and common fixed point theorems in symmetric spaces[J]. J Math Anal Appl,2006,320：352-360.

[3] Pant R P, Pant V. Common fixed points under strict contractive conditions[J]. J Math Anal Appl,2000,248:327-332.

[4] Jungck G. Compatible mappings and common fixed points[J]. Int J Math Math Sci,1986,9(4)：771-779.

[5] Jungck G, Moon K B, Park S,etal. On generalization of the Mier-Keeler type contraction maps[J]. J Math Anal Appl,1993,180：221-222.

[6] Jachymski J. Common fixed point theorems for some families of maps[J]. Indian J Pure Appl Math,1994,25：925-937.

[7] Jungck G. Common fixed points for noncontinuous non-self maps on nonmetric spaces[J]. Far East J Math Sci,1996,4(2):199-225.

[8] Pant R P. Common fixed points of sequence of mappings[J]. Ganita,1996,47:43-49.

[9] Pant R P. Common fixed points of contractive maps[J]. J Math Anal Appl,1998,226:251-258.

[10] Pant R P. R-weak commutativity and common fixed points[J]. Soochow J Math,1999,25:37-42.

[11] Wilson W A. On semi-metric spaces[J]. Amer J Math,1931,53:361-373.