一个基于辫群的密钥认证方案的安全分析
洪东招
(杭州师范大学 理学院,浙江 杭州 310036)
0 引 言
辫群这个概念于1925年由Artin引入[1],并于1947年严格定义了辫群[2].辫群上的数学困难问题,比如共轭搜索问题、共轭分解问题和求根问题等,非常适合作为密码学系统安全的基本困难假设.Anshel等人[3]和Ko等人[4]开创性地将辫群上的数学困难问题应用在密码学里,此后,人们开始广泛研究基于辫群的密码系统,许多基于辫群的密码学方案被提出来[5-13].
密钥认证在传统公钥密码体制中是非常重要的.在传统公钥密码系统中,每一个用户都有一个密钥对(公钥,私钥),公钥是公开的,攻击者可以替换用户的公钥,从而仿冒用户.那么,密钥认证的目的就是保证合法用户的公钥不能被伪造.因此,许多密钥认证方案被提出来[14-16].最近,卓等人[17]提出了基于辫群的密钥认证方案,然而,笔者将指出该方案的不安全性,易受公钥替换攻击,因而不满足用户公钥的不可否认性.通过改进原方案的注册和证书的生成和认证阶段,提出一个改进的方案,能有效抵抗密钥替换攻击,从而满足不可否认性.
1 文献[17]基于辫群的密钥认证方案
1.1 辫群简介
1.1.1 定 义
辫群Bn(n∈N)是由生成元σ1,σ2,…,σn-1生成的有限表示的非交换无限群,并且当n≥2时它的生成元满足如下关系:
当1≤i≤n-2时,σiσi+1σi=σi+1σiσi+1;当|i-j|≥2时,σiσj=σjσi,因此,辫群Bn可以表示为


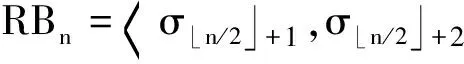
则称LBn为做左辫群,RBn为右辫群,且∀α∈LBn,∀β∈RBn,有αβ=βα成立.
1.1.2 性 质
辫群中的元素都可以通过标准形式来统一表示,即由p+1个参量(u,π1,π2,…,πp)表示,其中,u是整数;πi是个n阶置换,该表示是唯一的.
1.1.3 困难问题
1)共轭查找问题(Conjugacy Search Problem, CSP)
条件:x,y共轭,即(x,y)∈Bn×Bn,满足y=a-1xa,a∈Bn.
找到:b∈Bn,使得y=b-1xb.
2)一般共轭查找问题(General Conjugacy Search Problem, GCSP)
条件:(x,y)∈Bn×Bn,满足y=a-1xa,a∈Bm,m≤n.
找到:b∈Bn,使得y=b-1xb.
3)共轭分解问题(Conjugacy Decomposition Problem, CDP)
条件:(x,y)∈Bn×Bn,满足y=a-1xa,a∈Bm,m 找到:b1,b2∈Bm,使得y=b1xb2. 4)p次根问题(Root Problem, RP) 条件:(y,p)∈Bn×Z,满足y=xp,x∈Bn. 找到:b∈Bn,使得y=bp. 1.2 方案描述 1.2.1 初始参数 具有左标准型的辫群Bn(一个辫群称为是左标准型的,是指对于辫群中的2个辫元a,b,从a,b中猜出a或b是困难的),其中,n是偶数;4个整数s,t,LBs,RBt以及一个足够复杂的辫元x∈Bn. 1.2.2 密钥产生 用户选择p,q∈RZ+,p,q≥2,a∈LBs,计算X=apxaq,则(X,a)是用户的公私密钥对. 1.2.3 注册和证书的生成 在用户注册和生成证书的时候,将执行以下操作: 1)选择b∈RRBt作为自己的口令,且满足RP问题对于a,b是足够困难的,随机数r∈LBs. 2)计算W1=bp,W2=bq,Y1=b-1xb,Y2=r-1xr,Y3=b-1Y2b,令α=(W1,W2,Y3),β=(r,Y1). 3)将α,β秘密地提交给服务器,服务器将α存放在公开口令表中,β存放在秘密口令中. 4)用户生成证书C=apbpxbqaq,将X,C存放在公开密钥目录中. 1.2.4 认 证 1)服务器的认证.当服务器收到α,β后,计算Y4=r-1Y1r,如果Y3=Y4,则认为是用户提交的,否则,拒绝接收. 2)当有人(下称验证者)需要使用X来加密消息时,将检验用户的公开密钥证书,验证者执行的操作分两步: ①从公开密钥目录中得到用户的公钥X和证书C,从公开口令表中得到α; ②验证C=W1XW2,如果等式成立,则验证者承认公钥证书的正确性,就可以用X来加密消息,否则,他就拒绝X. 1.3 方案的不安全性 一个不诚实的用户可以伪造用户的公钥和证书,具体攻击如下: 1)选择c∈LBs计算:X′=cXc,C′=cCc 2)将看到C′和X′满足验证式: 从上述可知,验证式成立,如果使用X′来加密消息时,那么合法接收者无法解密密文,所以卓等人提出的基于辫群的密钥认证方案在公钥替换攻击下是不安全的,且不满足用户公钥的不可否认性. 为了克服上面的攻击,利用文献[16]的方法对基于辫群的密钥认证方案进行改进.初始参数和密钥产生阶段与原方案一样.在此修改原方案中注册和证书的生成阶段和认证阶段,具体的过程如下. 2.1 注册和证书的生成 前三步与原方案相同,主要改进的地方在第四步,在存放X,C之前,服务器分别对它们签名,而原方案是直接存放. 1)选择b∈RRBt作为自己的口令,且满足RP问题对于a,b是足够困难的,随机数r∈LBs. 2)计算W1=bp,W2=bq,Y1=b-1xb,Y2=r-1xr,Y3=b-1Y2b,令α=(W1,W2,Y3),β=(r,Y1). 3)将α,β秘密地提交给服务器,服务器将α存放在公开口令表中,β存放在秘密口令. 4)用户生成证书C=apbpxbqaq,将X,C提交给服务器,服务器分别计算X的签名SigS(X),C的签名SigS(C),然后存放在公开密钥目录中. 2.2 认 证 第一步与原方案相同,主要改进的地方在第二步,由于公开密钥目录存放的是公钥签名SigS(X)和证书签名SigS(C),所以首先要验证签名. 1)服务器的认证.当服务器收到α,β后,计算Y4=r-1Y1r,如果Y3=Y4,则认为是用户提交的,否则,拒绝接收. 2)当有人(下称验证者)需要使用X来加密消息时,将检验用户的公开密钥证书,验证者执行的操作分两步: ①从公开密钥目录中得到用户的公钥签名SigS(X)和证书签名SigS(C),从公开口令表中得到α; ②通过服务器的公钥验证SigS(X)和SigS(C)的正确性.如果正确,验证C=W1XW2,如果等式成立,则验证者承认公钥证书的正确性,就可以用X来加密消息,否则,他就拒绝X. 改进后的方案不仅具有原方案的安全性,而且还增加了原方案没有的安全性.由于在存放之前对用户公钥X和相应的证书C服务器对它们分别进行签名,并且攻击者不知道服务器的私钥,那么攻击者不能伪造服务器的签名SigS(X)和SigS(C),这使得攻击者不能伪造出能满足用户公钥验证式的用户公钥X和相应的证书C,所以改进后的方案能够抵抗公钥替换攻击. 文章已经证明卓等人提出的基于辫群的密钥认证方案是不安全的,不满足不可否认性,这对于密钥认证方案是致命的缺陷.通过对这个方案进行改进,能够抵抗公钥替换攻击,满足不可否认性.辫群的公钥密码学有着广阔的应用前景,人们已经开始寻求更加安全的、效率更高的、实用性更强的基于辫群的密码系统. [1] Artin E. Theorie der Zöpfe[J]. Abh Math Sem Univ Hamburg,1926,4:47-72. [2] Artin E. Theory of braids[J]. The Annals of Mathematics,1947,48(1):101-126. [3] Anshel I, Anshel M, Goldfeld D. An algebraic method for public-key cryptography[J]. Mathematical Research Letters,1999,6:287-291. [4] Ko K, Lee S, Cheon J,etal. New public key cryptosystem using braid groups[C]//Advances in Cryptology:Procedings of CRYPTO 2000, LNCS 1880. Berlin: Springer-Verlag,2000:166-183. [5] Lee E K, Lee S J, Halm S G. Pseudorandomness from braid groups[C]//Advances in Cryptology: Procedings of CRYPTO 2001, LNCS 2139. Berlin: Springer-Verlag,2001:486-502. [6] Anshel I, Anshel M, Fisher B,etal. New key agreement protocols in braid group cryptography[C]//Progress in Cryptology-CT-RSA 2001, LNCS 2020. Berlin: Springer-Verlag,2001:13-27. [7] Cha J C, Ko K H, Lee S J,etal. An efficient implementation of braid groups[C]//Advances in Cryptology: Proceedings of ASIACRYPT 2001, LNCS 2248. Berlin: Springer-Verlag,2001:144-156. [8] Ko K H, Choi D H, Cho M S,etal. New signature scheme using conjugacy problem[EB/OL] .(2002-11-11)[2009-11-19].http://eprint.iacr.org/2002/168.pdf. [9] Sibert H, Dehornoy P, Girault M. Entity authentication schemes using braid word reduction[EB/OL].(2002-12-13)[2009-11-07].http://eprint.iacr.org/2002/187.pdf. [10] Kim Z, Kim K. Provably-secure identification scheme based on braid groups[C/OL]//The 2004 Symposium on Cryptography and Information Security-SCIS 2004, Sendai, Japan,2004.[2009-11-10].http://caislab.kaist.ac.kr/Paper/paper_files/2004/SCIS04/scis2004%20-%20zeenkim.pdf. [11] Thomas T, Lal A K.Group Signature Schemes Using Braid Groups[EB/OL].(2006-02-17)[2009-11-05].http://arxiv.org/abs/cs/0602063. [12] Verma G K. A Proxy Blind Signature Scheme over Braid Groups[J]. International Journal of Network Security,2009,9(3):214-217. [13] Lai S, Verma V. Some Proxy Signature and Designated verifier Signature Schemes over Braid Groups[EB/OL].(2009-04-22)[2010-01-05].http://arxiv.org/PS_cache/arxiv/pdf/0904/0904.3422v1.pdf. [14] Shao Zuhua. A new key authentication scheme for cryptosystems based on discrete logarithms[J]. Applied Mathematics and Computation,2005,167(1):143-152. [15] Yoon E J, Yoo K Y . Improving the Sun-Cao’s Public Key Authentication Scheme for Non-repudiation[C]//Third International Conference on Intelligent Computing-ICIC 2007. Berlin: Springer-Verlag,2007:1103-1109. [16] Yoon E J, Yoo K Y. Secure Key Authentication Scheme Based on Discrete Logarithms[C]//Third International Conference on Next Generation Web Services Practices -NWeSP′07. New York: IEEE press,2007:73-78. [17] 卓泽朋,魏仕民,马陵勇.基于辫群的密钥认证方案[J].计算机工程,2009,35(13):139-140.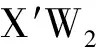
2 对文献[17]基于辫群的密钥认证方案的改进
3 安全分析
4 结 论

