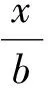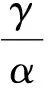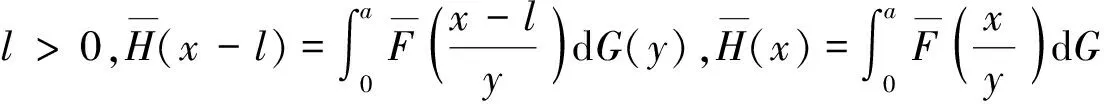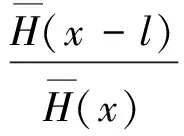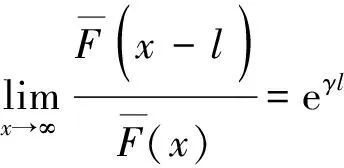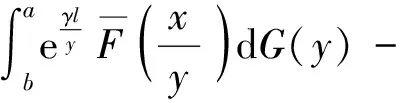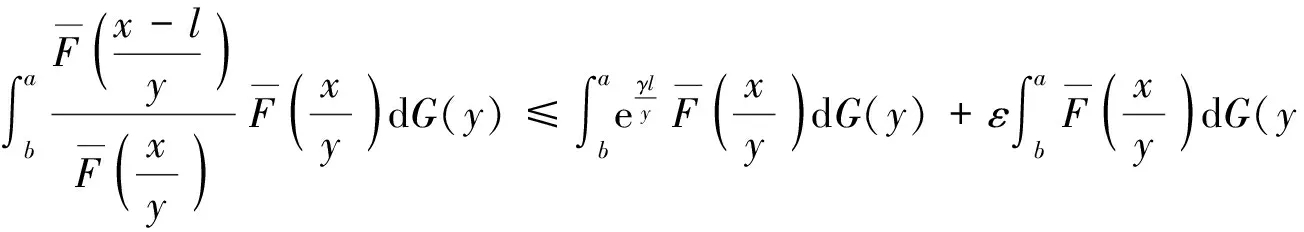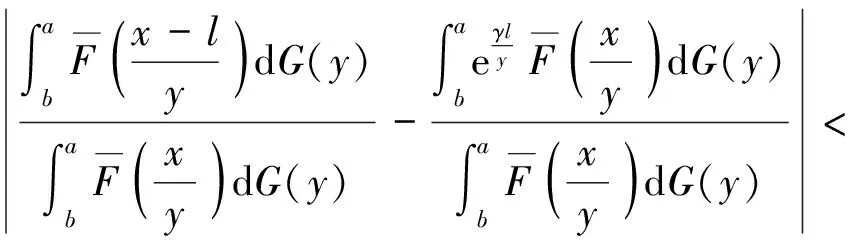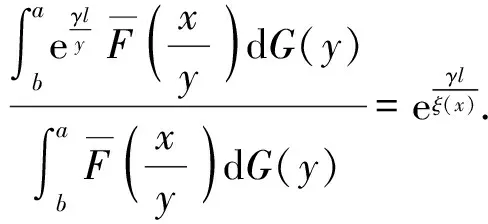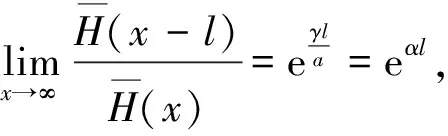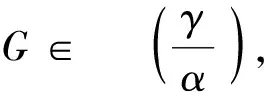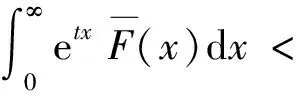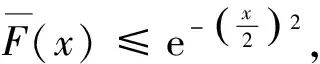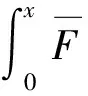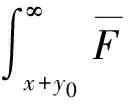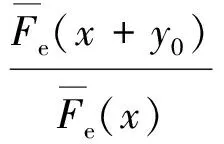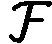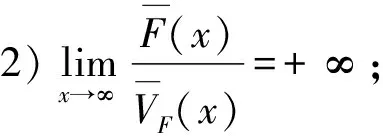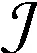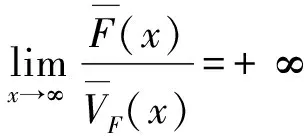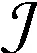非负轻尾分布族
刘 晓,王翠莲
(安徽师范大学 数学计算机科学学院,安徽 芜湖 241000)
0 引 言
由于随机变量尾分布的研究在分支过程、排队论、可靠性以及金融保险领域都有广泛的应用,因此自20世纪60年代以来,国外出现了大量的研究成果.至20世纪90年代的成果可参见Embrechts等[1].近年来,国内也出现了大量的相关文献,如苏淳等[2-4],王岳宝等[5].
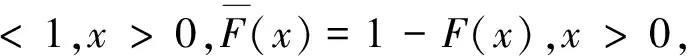
定义2称非负分布F属于(γ)族(γ≥0),若对任意l>0,都有

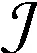
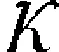
在金融保险业常会遇到相互独立的r.v.的乘积.例如,一张原始价值为X有价证卷,受到利率Y的影响后,实际价值增值为XY,通常可以假定X与Y相互独立,从应用的角度考虑,人们希望Y不要过多地影响本金X的性质,即XY的尾分布形状不要与X有太大差异,从而引进下述定义:
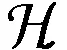

苏淳等[2]研究了(0)族的G稳定性,并给出:如果非负分布F∈(γ)(γ>0)且连续,则F*G∈(0)⟺G为无界非负分布;那么G有界为F*G∈(γ)(γ>0)的必要条件.
引理1若F∈(γ)(γ>0),则对任意0 定理1设非负分布F∈(γ)(γ>0)且连续,则H=F*G∈(α)(α>0)⟺且对任意b<有G(b)<1. 设0 (1) 其中 且 对∀ε>0,给定b,可适当取c,使 H3(x;a,b,c)<ε. (2) 另一方面, (3) 上面等号由引理1可得. 同理可得,对满足(2)的b,c,有 0 (4) (5) 从而 (6) 由ε的任意性知 注定理中必要性证明中没有用到F的连续性条件;若令其中的α=γ就得到F的G稳定性的充要条件.特别地,若G为单点分布有如下的推论成立. 推论若F∈(γ),G(a)=1(a>0),则F* 其中γ>1. 文章中研究的都是轻尾分布族,所以EX=μ<∞,引进函数: Fe(x)称为F(x)的均衡分布. 定理4下面3个命题等价: 1)⟹3).类似定理3的证明. [1] Embrechts P, Klüppelberg C, Mikosch T. Modelling extremal events for insurance and finance[M]. Berlin: Springer,1997:36-57. [2] 苏淳,陈昱.独立随机变量乘积的分布性状[J].中国科学,2006,36(2):161-178. [3] 苏淳,胡治水,唐启鹤.关于非负分布重尾程度的刻画[J].数学进展,2003,32(5):606-614. [4] Su Chun, Chen Jing, Hu Zhishui. Some discussions on the classL(γ)[J]. Journal of Mathematical Sciences,2004,122(4):3416-3425. [5] 王岳宝,成凤炀,杨洋.关于重尾分布间的控制关系及其应用[J].应用概率统计,2005,21(1):21-30.