中学数学要加强“形同质异”的辨析教学
●(保定外国语学校 河北保定 071000)
在数学教学中经常会遇到一类形式相同但本质相异的问题,学生极易受形似的迷惑将他们混为一谈,因此必须加强“形同质异”的辨析教学.具体说来,在平时练习或测试时可将这类问题放在一起讨论,通过认真对比分析,充分暴露出他们之间细微但又属于本质的差异,这必将大大提高学生分析问题、解决问题的能力.现举例说明之.
1 定义域与有意义

(1)f(x)在区间(-∞,1]上有意义;
(2)f(x)的定义域为(-∞,1].
请分别求出满足条件(1)和条件(2)的a的取值范围.
辨析与解答 不少学生误认为这2道题是一样的,其实截然不同.条件(1)只说f(x)在(-∞,1]上有意义,并未说明其定义域就是(-∞,1].若定义域为集合A,则只能得到(-∞,1]⊆A.条件(2)则明确指出f(x)的定义域就是(-∞,1],因此这2道题有着迥然不同的解法.
(1)由题意可得




或

于是

结合题意得

解得
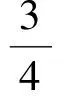
2 函数值变化范围与函数值域
题组2 (1)函数y=3x2-(2m+6)x+m+3的值恒为非负数,求实数m的取值范围;
(2)函数y=3x2-(2m+6)x+m+3的值域为非负实数,求实数m的取值范围.
辨析与解答 这2道题实在太像了!但经仔细辨析,发现有本质差异:在第(1)小题中,“函数y=3x2-(2m+6)x+m+3的值恒为非负数”是指“当自变量x在定义域内取一切值时,所对应的函数y的每一个值都必须大于等于0,但不一定要求y必须取到大于0的一切数”.而在第(2)小题中,“函数y=3x2-(2m+6)x+m+3的值域为非负实数”是指“当自变量x在定义域内取一切值时,所对应的函数值必须且只能取到一切大于等于0的数”.由此可见,两者貌似相同,实则迥异.
(1)由题意得,y=3x2-(2m+6)x+m+3≥0(m∈R)恒成立,因此关于x的函数的二次项系数3>0,于是
Δ=(2m+6)2-4×3(m+3)≤0,
解得-3≤m≤0,故m的取值范围是[-3,0].
(2)通过上面分析可知,应满足
Δ=(2m+6)2-4×3(m+3)=0,
解得
m=-3或m=0,
即使函数y=3x2-(2m+6)x+m+3的值域为非负实数的m的值为-3或0.
3 奇数位必须是奇数与奇数必须在奇数位
题组3 从1,2,3,4,5,6,7,8,9这9个数字中任取5个组成无重复数字的5位数.(1)奇数位必须是奇数;(2)奇数必须在奇数位.分别求出满足条件(1)和条件(2)的5位数的个数.
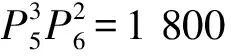

4 对任意x恒成立与存在x成立
题组4 (1)若任意x∈[1,3],使得不等式mx2+(m-3)x-3>0恒成立,求实数m的取值范围;
(2)若存在x∈[1,3],使得不等式mx2+(m-3)x-3>0恒成立,求实数m的取值范围.
辨析与解答 原不等式可化为
(x2+x)m>3(x+1).
由x∈[1,3],得
x2+x>0,
从而
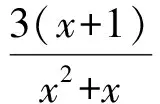
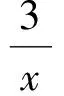
对于第(1)小题,由题意可得m>[f(x)]max=3.而对于第(2)小题,由题意可得m>[f(x)]min=1.这正与恒成立问题相反,很容易混淆,应注意区分,以免出错.
5 函数递增与数列递增
题组5 (1)设函数f(x)=x2+kx在[1,+∞)上是单调递增函数,求k的取值范围;
(2)若数列{an}的通项公式为an=n2+kn,且满足an 辨析与解答 乍看2道题似乎一样,我们注意寻求它们的“异”.第(1)小题的图像是连续的,而第(2)小题的图像是离散的,2道题都可以利用二次函数的图像求解,都是考虑对称轴与区间的关系,但是其区间是不同的。 题组6 (1)若函数f(x)=x2-(3a-1)x+a2在[1,+∞)单调递增,求实数a的取值范围; (2)若函数f(x)=x2-(3a-1)x+a2的单调递增区间是[1,+∞),求实数a的取值范围. 辨析与解答 单调区间与区间单调是2个截然不同的概念.若函数f(x)在区间M上具有单调性,则在M的任一区间上f(x)具有相同的单调性,单调区间是其中最大的区间. 题组7 (1)若函数y=lg(ax2+2x+a)的定义域为R,求实数a的取值范围. (2)若函数y=lg(ax2+2x+a)的值域为R,求实数a的取值范围. 辨析与解答 (1)函数y=lg(ax2+2x+a)的定义域为R,即无论x为何实数,ax2+2x+a>0恒成立.令f(x)=ax2+2x+a,则f(x)的图像应始终在x轴的上方,因此a>0且Δ=4-4a2<0,解得a>1. (2)函数y=lg(ax2+2x+a)的值域为R,就是f(x)=ax2+2x+a要取遍一切正实数.当a=0时,f(x)=2x符合要求;当a>0时,Δ=4-4a2≥0,解得0 题组8 (1)对于任意x∈[0,4],不等式x2+ax≥4x+a-3恒成立,求实数a的取值范围; (2)对于任意a∈[0,4],不等式x2+ax≥4x+a-3恒成立,求实数x的取值范围. 辨析与解答 (1)原不等式可转化为f(x)=x2+(a-4)x-a+3≥0恒成立. 综上所述,满足条件的a的取值范围是{a|a=2}. (2)不等式可转化为对任意a∈[0,4],不等式f(a)=(x-1)a+x2-4x+3≥0恒成立. 当x=1时,对任意a∈[0,4],f(a)=0,原不等式恒成立. 当x≠1时,只要f(x)min≥0即可,因此 解得 x≤-1或x≥3. 故满足条件的x的取值范围是{x|x≤-1或x=1或x≥3}. 题组9 (1)已知y=2x-x3,求以点P(1,1)为切点的切线方程; (2)已知y=2x-x3,求过点P(1,1)的切线方程. 辨析与解答 这2道题的区别在于:第(2)小题包含第(1)小题的情况,而且除此之外,还有经过点P但不以其为切点的切线方程. (1)y′=2-3x2,于是k=-1,切线方程为y-1=-(x-1),即x+y-2=0为所求. (2)当点P为切点时,同第(1)小题,可得切线方程为x+y-2=0. 当P不是切点时,设切点为Q(m,n),依题意可得 解得 因此以点Q为切点的切线方程为5x-4y-1=0. 综上所述,满足条件的切线方程为 x+y-2=0或5x-4y-1=0. (1)若函数y=f(x)满足f(x+a)=f(b-x),则函数y=f(x)的对称轴方程是________; (2)函数y=f(x+a)与函数y=f(b-x)的图像关于________对称. 辨析与解答 这2道题目极易混淆.事实上,第(1)小题是考查一个函数自身图像的对称性的.而第(2)小题则是考查2个函数图像之间的对称性的. (1)在函数y=f(x)的图像上任取一点P(x0+a,y0),得 y0=f(a+x0)=f(b-x0), (2)在函数y=f(x+a)的图像上任取一点P(x0,y0),得 y0=f(a+x0)=f[b-(b-a-x0)], 题组11 已知函数y=f(x). (1)若f(x)的定义域为[2,3],求f(x+1)的定义域; (2)若f(x+1)的定义域为[2,3],求f(x)的定义域. 辨析与解答 对于第(1)小题,学生一般都知道该怎么做,而对于第(2)小题,许多学生不知道由函数f(x+1)的定义域如何求f(x)的定义域.其原因是:他们不明白在同一法则下,作用的对象可以不同,但对象的范围必须相同. (1)由f(x)的定义域为[2,3],得 2≤x+1≤3, 从而1≤x≤2,因此f(x+1)的定义域[1,2]. (2)由f(x+1)的定义域为[2,3],得 2≤x≤3, 即 3≤x+1≤4, 于是f(x)的定义域为[3,4]. 在数学中,“形同质异”的问题是大量存在的,而学生对此往往有一种“亲切”感,易于产生放松麻痹的心态,从而造成解题失误.在教学中,通过对“形同质异”问题的对比与研究,透过“外貌”颇似的表层,必定能使学生逐渐澄清各种模糊概念,深入认识实质,深化巩固并掌握知识,防止知识负迁移,从而能够从各种“形式相同”的问题中抓住“实质不同”的要害,找到解决问题的正确途径.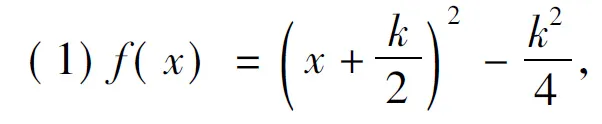
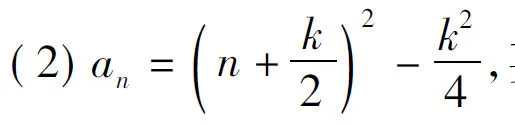
6 单调区间与区间单调


7 定义域与值域
8 主元与次元
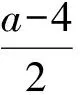
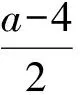

9 以点P为切点的切线方程与过点P的切线方程
10 函数的自对称与两函数之间的对称题组10



