基于 SV M和遗传算法的纸浆间歇蒸煮参数优化方法
沈正华 黄锦华 宋 超 杨春节
(1.浙江大学工业控制技术国家重点实验室,浙江杭州,310027)(2.福建青山纸业股份有限公司,福建三明,365500)
基于 SV M和遗传算法的纸浆间歇蒸煮参数优化方法
沈正华1黄锦华2宋 超1杨春节1
(1.浙江大学工业控制技术国家重点实验室,浙江杭州,310027)(2.福建青山纸业股份有限公司,福建三明,365500)
为降低纸浆间歇蒸煮过程的能耗,提出了一种基于支持向量机 (SVM)和遗传算法的蒸煮参数优化方法。该方法先根据生产数据,采用 SVM建立了间歇蒸煮纸浆卡伯值模型,描述了白液浓度、硫化度、白液量、黑液量、蒸煮时间和蒸煮温度等参数与纸浆卡伯值之间的数学关系;再针对基于 SVM的纸浆卡伯值模型较难用于常规优化方法的问题,提出了一种改进的自适应小生境遗传算法,用于间歇蒸煮的参数优化,使纸浆满足质量要求的前提下尽量降低蒸煮过程能耗;最后进行仿真,与实际生产数据相比,实验结果节约蒸汽 3.52%,节约白液用量 17.18%,硫化度减少 0.37%。实验结果表明,该方法模型泛化性好,优化效果明显,很大程度上实现了节能降耗。
间歇蒸煮;支持向量机;自适应交叉;小生境;遗传算法
蒸煮是将原料置于反应釜 (蒸球或蒸煮锅),在一定的温度、压力和化学药液的作用下,经过复杂的化学反应,脱去原料中木素,分离出纤维素,形成纸浆[1]。蒸煮作为造纸过程的一个重要准备工段,在很大程度上决定了质量,而且整个蒸煮过程具有高能耗、高物耗与高污染等“三高”特点[2]。所以很有必要对蒸煮过程的参数进行优化。影响蒸煮质量、蒸煮成本、蒸煮能耗的因素有很多,比如原料的品种和质量、白液浓度、白液用量、黑液用量、硫化度、蒸煮时间、蒸煮温度等。自从 Vroom提出 H因子动力学模型以来,蒸煮过程的模型描述有上百种,有机理模型、经验模型、回归模型等,但都不具有通用性。而且现有的文献资料中,没有将影响蒸煮的所有可变参数集中在一起研究,即一般都是将几个可变参数作为固定常数,然后对剩下的参数进行建模与优化,得到的也是局部最优解。
本研究根据福建某造纸厂的现场数据,建立了一个较全面的间歇蒸煮卡伯值模型,考虑了白液浓度、白液用量、黑液用量、硫化度、蒸煮时间和蒸煮温度等蒸煮参数,期望能更好地反映蒸煮规律。
对于蒸煮工艺参数优化问题,主要有两种方法:第一种是采用试探性实验,但这种方法人为因素较多,得出的最优工艺参数未必是实际最优的参数,实际应用较少;第二种则是通过建模分析,根据建立的模型,采用优化工具得到最优的参数曲线。第二种方法研究应用的较多,肖兰等[3-4]根据回归化后的模型,用非线性规划的方法对蒸煮时间和有效碱浓度寻优,但是没有考虑蒸煮的其他参数;鄢烈祥等[5]用神经网络降维分析法把制浆蒸煮工艺过程的样本数据降维映射到二维空间上,并生成纸浆得率和硬度的等值线,由此确定出控制纸浆硬度在一定范围内而纸浆得率较高的操作区域,但是这种方法精确度不高;吴新生等[6]采用神经网络模型,在输入变量变化范围内均匀取出 n个点,求出这 n个点的输出,再通过比较这些输出得出最优输入,这种寻优方式不具导向性,得出来的结果未必最优;金福江等[7-8]对连续蒸煮器和间歇蒸煮器都建立了回归模型,并用模糊逻辑决策等方法对其进行优化,但是没有考虑有效碱浓度、硫化度等,且对模型做了大量简化。
本研究根据造纸蒸煮模型的特点,设计了一种改进的自适应小生境遗传算法,融入小生境技术和自适应交叉变异技术,既能保证种群多样性,又能保证解的收敛性,从而增强了整个算法的局部寻优和全局搜索能力。
1 间歇蒸煮模型
支持向量机 (SupportVector Machine,SVM)作为一种新型的学习机器,具有拓扑结构简单、泛化能力强、提供全局最优解等优点[9],因此,本研究采用 SVM来建立间歇蒸煮卡伯值模型。
福建某造纸厂生产纸袋纸的蒸煮原料是马尾松,采用硫酸盐法间歇蒸煮,本研究利用现场生产数据建立了非线性支持向量机模型。SVM的输入是白液浓度、硫化度、白液用量、黑液用量、蒸煮时间、蒸煮温度,输出是卡伯值。本研究将 6个输入一并考虑,希望所建得的模型更全面具体地反映实际蒸煮过程。用 75组数据进行模型训练,20组数据进行仿真测试,得到的仿真结果如图1和表1所示。从图1可知,卡伯值仿真值和真实值均匀地分布在 Y=X这条直线上,从表1可知,卡伯值真实值与仿真值相对误差在 0.016以内,说明模型的泛化性较好,精确性较高。
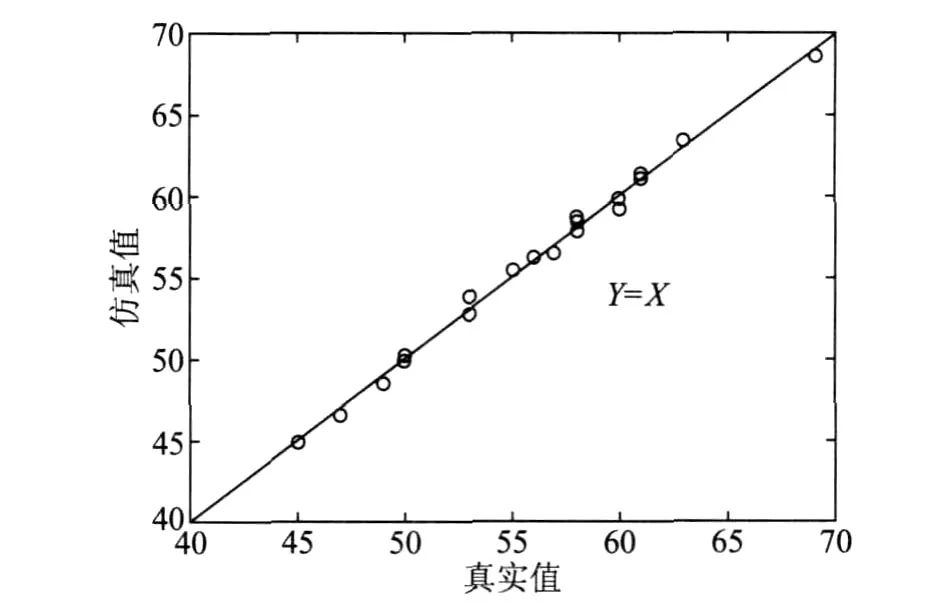
图1 间歇蒸煮 SVM模型卡伯值仿真值与真实值对比
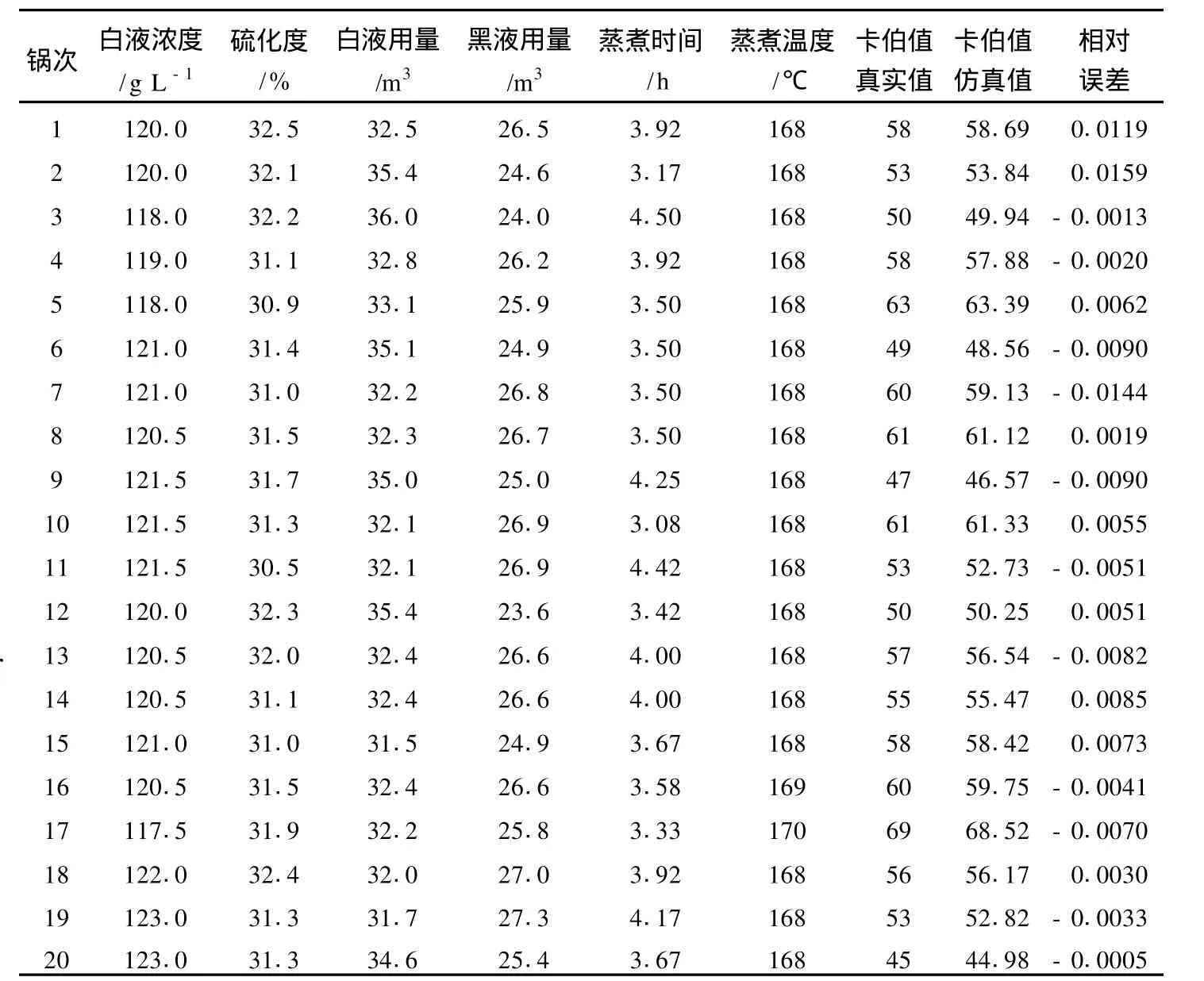
表1 间歇蒸煮 SVM模型输出结果
2 改进的自适应小生境遗传算法
标准遗传算法 (Standard Genetic Algorithm,简称 SGA)存在容易早熟收敛、局部寻优能力差、后期进化较慢和近亲繁殖等缺点。本研究根据纸浆蒸煮模型特点,设计改进的自适应小生境遗传算法,融入小生境技术和自适应交叉变异技术,既能保证种群多样性,又能保证解的收敛性,从而增强了整个算法的局部寻优和全局搜索能力。
2.1 初始种群的产生
为了提高全局搜索成功的概率,必须保证初始种群的多样性,并希望能够均匀地分布于整个解空间。故将自变量空间分成 ns个子区间,每个子区间随机地产生N个个体,共组成 ns个子种群,每个子种群有N个个体。
2.2 基于最优保存策略的选择操作
经理论研究证明,最优保存策略能够保证全局收敛性。取当前种群中适应度最高的 10%个体不参加交叉与变异运算,直接保存到下一代群体中,其他个体进行选择交叉变异操作产生下一代个体,用保留的个体来替换掉下一代个体中适应度最低的那部分个体。
2.3 自适应交叉操作
交叉操作根据个体的适应度大小和交叉个体的距离而定,分为境内交叉和境外交叉。
境内交叉保证解的收敛性和精确性,为了找到小生境内更好的解,进行如下操作:对于每个小生境内前 10%个体进行境内交叉,对于其中任选的两个个体,当欧式距离 L小于等于 radius1时,给予较大的交叉概率,当欧式距离 L大于 radius1时,给予较小交叉概率。同时,根据个体的适应度,采用 Srinvivas等[10]提出的自适应交叉算子,交叉算子由式 (1)和式 (2)得到:
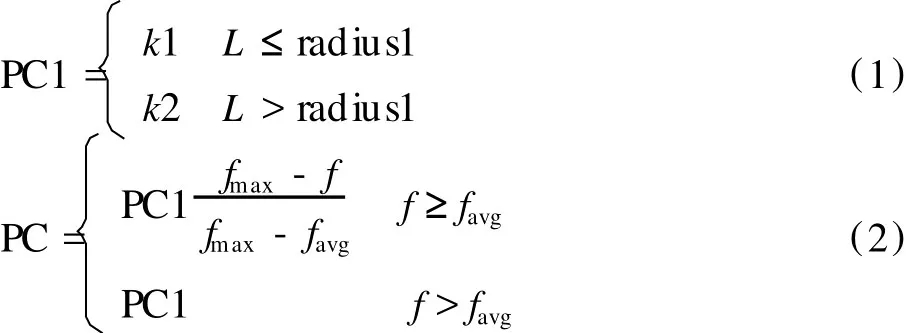
其中,k1、k2为常数,k1>k2;L为小生境内两个个体的欧式距离;PC1为计算交叉概率的中间变量;PC为两个个体的交叉概率;f为两个交叉个体中适应度较大的个体的适应度;fmax是小生境内的最大适应度;favg为小生境的平均适应度。
境外交叉保证解的多样性,希望通过两个欧式距离较大的个体的交叉利用“杂交优势”产生出新的最优解,具体如下:对每个小生境内后 90%个体进行境外交叉,对于种群中任选的两个个体,当欧式距离 L小于等于 radius1时,给予较小的交叉概率,当欧式距离 L大于 radius1时,给予较大交叉概率。同时,根据个体的适应度,采用自适应交叉算子,交叉算子由式 (3)和式 (4)得到:
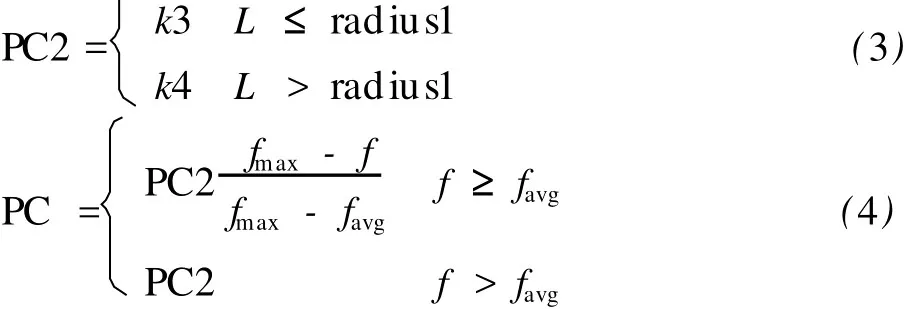
其中,k3、k4为常数,k3 采用浮点数编码,境内交叉和境外交叉都采用单点交叉,随机产生交叉位,对交叉位上的基因采用式(5)交叉操作: 采取高斯变异,同时,高适应度的个体以较小概率变异,低适应度的个体以较大概率变异。随机产生变异位,变异操作如式 (7)和式 (8): 其中,Pm为变异概率;Pm1为常数;f是个体的适应度;fmax是所有个体中的最大适应度;favg为所有个体的平均适应度;X′k为变异的新个体的第 k个基因,为第 k个基因位的变异下限,为第 k个基因位的变异上限,r是随机产生的 [0,1]区间的数。 根据个体的适应度和个体间距离进行小生境划分,对于经过选择交叉变异后的种群,计算每个个体的适应度,并对个体进行适应度排序,以其中适应度最大个体为中心,radius2为半径,选取第一个小生境的个体,再在剩下的个体中,以适应度最大个体为中心,radius2为半径,选取第二个小生境的个体,依此类推,直到取完所有个体,这样就形成了众多小生境,每个小生境的分布密度和个体数目都不一样。 ①初始种群产生:用上述方法产生初始种群,记标记矩阵 S为{S(1),S(2),…S(ns)},其中,ns为小生境个数,S(i)为每个小生境的个体数目。 ②计算每个个体的适应度,并在小生境内对个体进行适应度排序。 ③最优保存策略:取所有个体中前 10%最好个体,组成矩阵 BestChrom。 ④选择操作:在每个小生境内对个体进行选择操作,得到新的种群。 ⑤交叉操作:分别进行境内交叉和境外交叉。 ⑥变异操作:按式 (7)和式 (8)进行变异。 ⑦小生境划分:将经过选择交叉变异之后的种群记为 SelCh,将 SelCh和 BestChrom组成 Chrom={BestChrom;SelCh},对 Chrom进行小生境划分,更新标记矩阵 S。 ⑧判断是否满足算法终止条件,若不满足条件,则返回第③步;否则,结束种群进化,输出最优值。 采用常用的遗传算法 (GA)性能测试函数 shubert函数进行仿真测试,shubert函数有 760个局部最优点,18个全局最优点,全局最优解的目标函数值是 f(x1,x2) =-186.7309,shubert函数具体形式如式 (9)和式 (10)所示: 表2 用 shubert函数仿真结果对比 用 SGA和本算法分别对 shubert函数进行优化,两种算法独立运行 30次,仿真结果统计如表2所示。从表2可以看出,本算法的收敛性和误差明显好于SG A。而且,SGA找到最优解附近要 30多代,并且有时会陷入局部最小解,而本算法收敛很快,十几代后就找到了最优解附近。 将如前所述的 SVM模型和改进的自适应小生境遗传算法应用于间歇蒸煮参数优化,优化性能指标为: ①纸浆满足质量要求,即卡伯值 (公式中卡伯值用 K表示)在一定范围内: 卡伯值由式 (13)所示的支持向量机模型得到: K=svm (W lc,S,W ld,Bld,td,Td) (13) 其中,W lc为白液浓度 (White Liquid Concentration),S为硫化度,W ld为白液用量 (White Liquid dosage),Bld为黑液用量 (Black Liquid dosage),td为蒸煮时间,Td为蒸煮温度。 ②蒸汽能耗少: 其中,Qneed为蒸煮 1锅纸浆需要的热量,Q1为蒸煮锅内绝干木片吸收的热量,Q2为木片中水分吸收的热量,Q3为白液吸收的热量,Q4为黑液吸收的热量,Q5为蒸煮锅的热量、蒸煮锅保护层热量、放汽阶段放走的热量以及蒸煮锅辐射热的总和,根据福建某造纸厂日常蒸煮数据估算,Q5=987154.8 kcal(1 cal=4.1868 J)。C1、C2、C3、C4分别为绝干木片、木片水分、白液、黑液的比热容,C1=0.33 kcal/(kg·℃),C2=1 kcal/(kg·℃),C3=0.91 kcal/(kg·℃),C4=0.91 kcal/(kg·℃)。M1为绝干木片装锅量,M1=17271 kg;M2为木片含水量,木片水分为 40%,所以M2=17271×40% ÷(1-40%)=11514 kg;M3为白液质量,白液密度为 1.10 kg/L,所以,M3=1100×W ld;M4为黑液质量,黑液密度为 1.11 kg/L,所以,M3=1110×Bld。Td为蒸煮最高温度;T0为木片初始温度;T0取 20℃;T1为白液初始温度;T2为黑液初始温度。根据该厂日常数据统计,T1=75℃,T2=80℃。 表3 间歇蒸煮优化结果 ③白液用量少,即节约物耗: 间歇蒸煮参数优化是一个有等式约束和不等式约束的优化问题: ①不等式约束:硫化度、白液浓度、白液用量、黑液用量、蒸煮温度、蒸煮时间必须满足一定范围; ②等式约束: 用罚函数的思想来处理等式约束,对在解空间中无对应可行解的个体计算适应度时,处以一个罚函数,从而降低个体的适应度,使该个体遗传到下一代群体中的概率减小。具体如式 (22): 根据以上分析,优化模型转化为: 将改进的自适应小生境遗传算法运用于该优化模型,运行数次后的平均优化结果如表3所示。 福建某造纸厂每锅产量约为9.2 t绝干浆,蒸汽用量是 1.8 t/t浆,则每锅需要蒸汽为 9.2×1800=16560 kg,蒸汽温度是 180℃,蒸汽潜热是 663.4-180=483.4,所以,蒸汽能耗为 16560×483.4=8005.10Mcal。另外,根据该厂日常生产数据分析,加入白液量平均为 32.37 m3,硫化度为 27.64%。本研究优化结果:蒸汽能耗为 7723.54 Mcal,硫化度为27.54%,白液用量仅为 26.81 m3,节约蒸汽 3.52%,节约白液用量 17.18%,硫化度减少了 0.37%,硫化度减少了,意味着Na2S用量也减少了。 支持向量机理论为纸浆蒸煮过程建模提供了有效的方法。本研究所建立的纸浆卡伯值模型能准确地反映白液浓度、硫化度、白液用量、黑液用量、蒸煮时间和蒸煮温度等蒸煮参数与纸浆卡伯值之间的数学关系,为间歇蒸煮参数优化奠定了良好的基础。同时,改进的自适应小生境遗传算法为间歇蒸煮参数优化问题提供了一种有效的求解方法,优化效果良好,对于降低蒸煮过程能耗具有重要意义。 [1] 福建林学院.木材制浆工艺学 [M].北京:中国林业出版社,1986. [2] 杨春节,何 川,宋执环.基于近红外光谱与支持向量机的纸浆卡伯值在线测量 [J].光谱学与光谱分析,2008,28(8):1795. [3] 肖 兰,王 慧,李 平.基于过程建模与优化技术的清洁生产策略 [J].浙江大学学报:自然科学版,1998,5:777. [4] 许向阳,于 玲,祝和云,等.间歇蒸煮过程计算机优化控制系统 [J].中国造纸学报,2000,15:98. [5] 鄢烈祥,聂 青.神经网络降维分析法用于制浆蒸煮工艺条件的优化 [J].中国造纸学报,2000,15:10. [6] 吴新生,刘焕彬,谢益民,等.基于人工神经网络方法的间歇硫酸盐法蒸煮纸浆硬度的 H-因子控制 [J].广东造纸,1998(2):5. [7] 金福江.制浆生产蒸煮过程多目标优化控制 [J].华侨大学学报:自然科学版,2001,22(4):422. [8] 金福江,王 慧,李 平.间歇蒸煮过程的分层多目标优化 [J].中国造纸学报,2002,17(1):86. [9] 杜树新,吴铁军.用于回归估计的支持向量机方法 [J].系统仿真学报,2003,15(11):1580. [10] SrinivasM,Patnaik L M.Adaptive Probabilities of Crossover and Mutation in Genetic Algorithms[J].IEEE Trans on System,Man,and Cybemetics,1994,24(4):656. Opt im ization of Batch Cooking Parameters Based on SVM and Genetic Algorithm SHEN Zheng-hua1HUANGin-hua2SONG Chao1YANG Chun-jie1,* In order to reduce energy consumption of batch pulpingprocess,amethod based on SupportVectorMachine(SVM)and improved Genetic Algorithm is proposed.According to the production data of a pulp mill in Fujian province,a SVM model of kappa number is developed,which accurately reflects the relationship between kappa number and cooking parameters,namelywhite liquor concentration,sulfidity,white liquor dosage,black liquor dosage,cooking time and cooking temperature.Because it is difficult to use SVM model in conventionaloptimization approach,this paper presents an improved Genetic Algorithm using niching technology and adaptive crossover technology,which realizes energy conservation and consumption reduction on the premise of guaranteeing the pulp's quality.Finally,this method is used in a mill in Fujian province.The simulation results showed that it saved 3.52%of steam,17.18%ofwhite liquid dosage and 0.37%of sulfidity,comparing to realproduction data.The s imulation results showed good generalization ability and precision of themodel and also good performance of this opt imization approach that can realize energy consumption reduction definitely. batch cooking;SVM;adaptive crossover;niching technology;Genetic Algorithm TS71;TP27 A 0254-508X(2010)10-0001-05 沈正华女士,在读硕士研究生;主要研究方向:复杂系统建模与控制。 (* E-mail:cjyang@iipc.zju.edu.cn) 2010-05-18 国家 “863”计划项目资助 (No.2007AA041406)。 (责任编辑:常 青)


2.4 变异操作
2.5 小生境划分
2.6 算法流程
2.7 仿真结果


3 SVM模型和改进的自适应小生境遗传算法用于间歇蒸煮参数优化

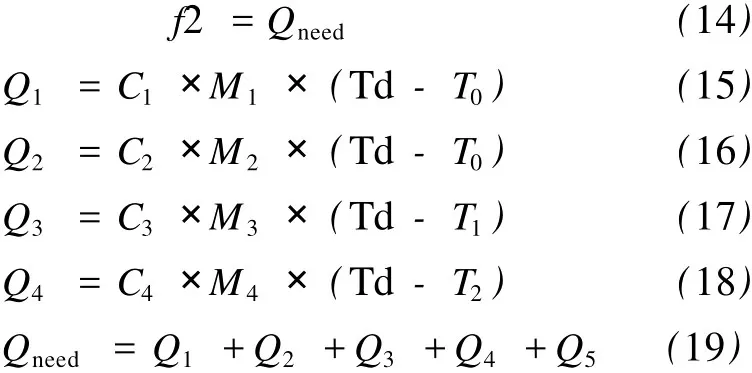


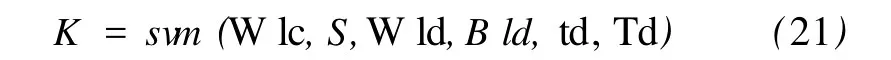

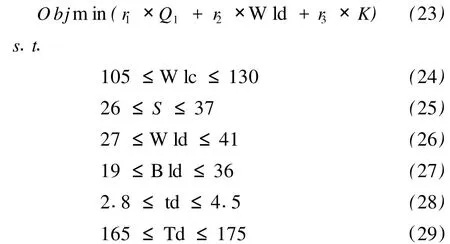
4 结 论
(1.State Key Lab of Industrial Control Technology,Zhejiang University,Hangzhou,Zhejiang Province,310027;2.Fujian Q ingshan Paper Industry Co.,Ltd.,Sanm ing,Fujian Province,365500)
——以贵阳花溪公园为例

