二重极限求解方法探析

齐春泽

（兰州商学院 信息工程学院，甘肃 兰州 730020）

二重极限求解方法探析

齐春泽

（兰州商学院 信息工程学院，甘肃 兰州 730020）

极限运算是数学分析中较重要的一种运算。本文主要介绍了求解二重极限的几种方法，针对各种方法给出了典型例题。

多元函数；二重极限；累次极限

多元函数的重极限是多元函数极限理论的重要内容，是多元函数微积分的重要基础。多个独立变化的自变量使得多元函数重极限难以求解，而正确的求解方法不仅降低了求解的难度，也提高了求解的速度。

一、用定义验证法求解[1]

先求出一个累次极限，该累次极限是否为二重极限，再用定义验证。

例1 设

二、利用性质运算的方法求解[2]

1. 函数在连续点的极限与一元函数一样仍等于连续点的函数值。

2. 二元函数极限四则运算仍然成立。

3. 有界函数与无穷小量之积仍为无穷小量。

4. 可利用两个重要极限。

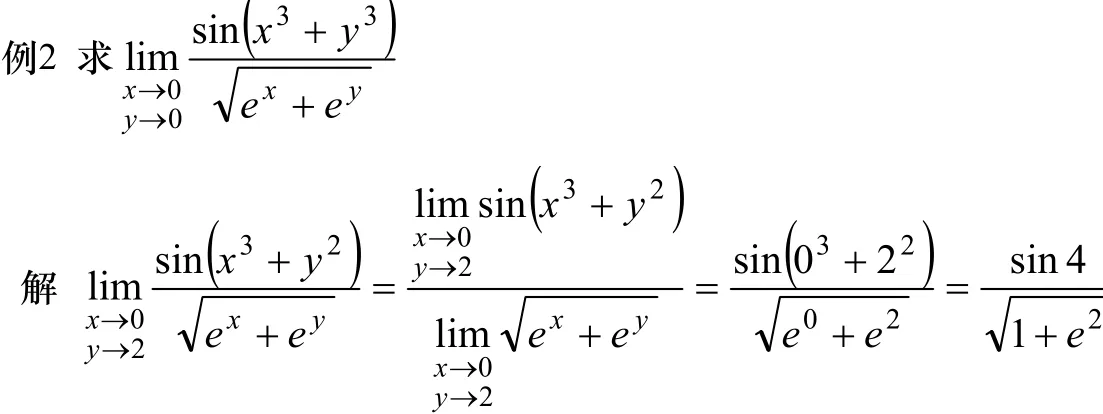
三、用变量代换的方法求解[2][3]

利用变量代换把二重极限化为一元函数的极限或化为易于求解的二重极限，从而求得结果。

四、用多元函数收敛判别法的方法求解[4]

通过放缩法使二元函数夹在两个已知极限的函数之间，再利用两边夹定理，推出结果。

五、利用复合函数求解[3]

定理 若函数 u =ϕ( x , y ), v =φ(x ,y )于点 P0( x0,y0)存在极限,并且函数 f ( u , v ) 于点 (u0,v0)连续 其中

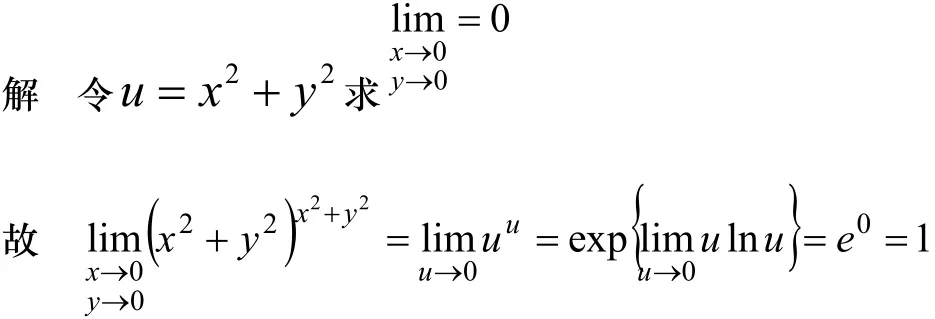
六、利用累次极限求解[4]

综上所述，可以把一元函数极限的求法推广到二元函数，但是在求解过程中要具体问题具体分析，要理解问题的本质，用最简便，最合理的方法来解决二重极限的求解问题。

[1]同济大学数学教研室. 高等数学[M].第4 版. 北京:高等教育出版社,1996.

[2]刘玉琏,傅沛仁. 数学分析讲义[M].第3 版. 北京:高等教育出版社,1992.

[3]孙涛. 数学分析经典习题解析[M].北京:高等教育出版社,2004.

[4]费定晖，周学圣．数学分析习题集题解（五）[M]．济南：山东科学技术出版社，2001.

O172

A

1673-2219（2010）12-0001-03

2010－08－22

齐春泽（1980－），女，浙江天台人，讲师，硕士。

（责任编校：何俊华）