基于不确定性AHP和群决策理论的港口岸线等级评价模型

蒋 军

(重庆交通大学交通运输学院，重庆400074)

近年来，随着我国国民经济和对外贸易的高速发展，港口岸线的区位优势得到了更加明显的体现。为适应这一趋势，我国许多港口城市不断新建或改扩建码头泊位，取得了骄人的业绩。但也暴露出了工程建设时缺乏对岸线利用的合理规划，出现了深水岸线浅用、港口建成后“晒太阳”或维护费用太高等诸多问题。因此，在港口工程建设前，对港口岸线等级进行综合评价，并提出不同等级岸线的建设使用意见就显得尤为重要。然而，传统的评价方法大多存在评价指标不够全面，评判过程过于主观化等弊端。因此，笔者在全面分析影响港口岸线等级优劣因素的基础上，拟定出全面且有代表性的指标。在确定评价指标权重时引入不确定性层次分析法(AHP)和群决策理论，以期使评价结果更具科学性和可信性。

1 评价指标的选取

港口岸线等级评价是一个多因素的系统评价问题，其涉及的评价指标和因素很多，本着全面性、代表性、可行性等原则，笔者从政策法规、自然条件、经济、交通区位、配套服务等方面选取了影响港口岸线等级优劣的评价指标［1－4］，详见表 1。

表1 港口岸线等级评价指标体系Tab.1 Evaluation index system of the waterline classes

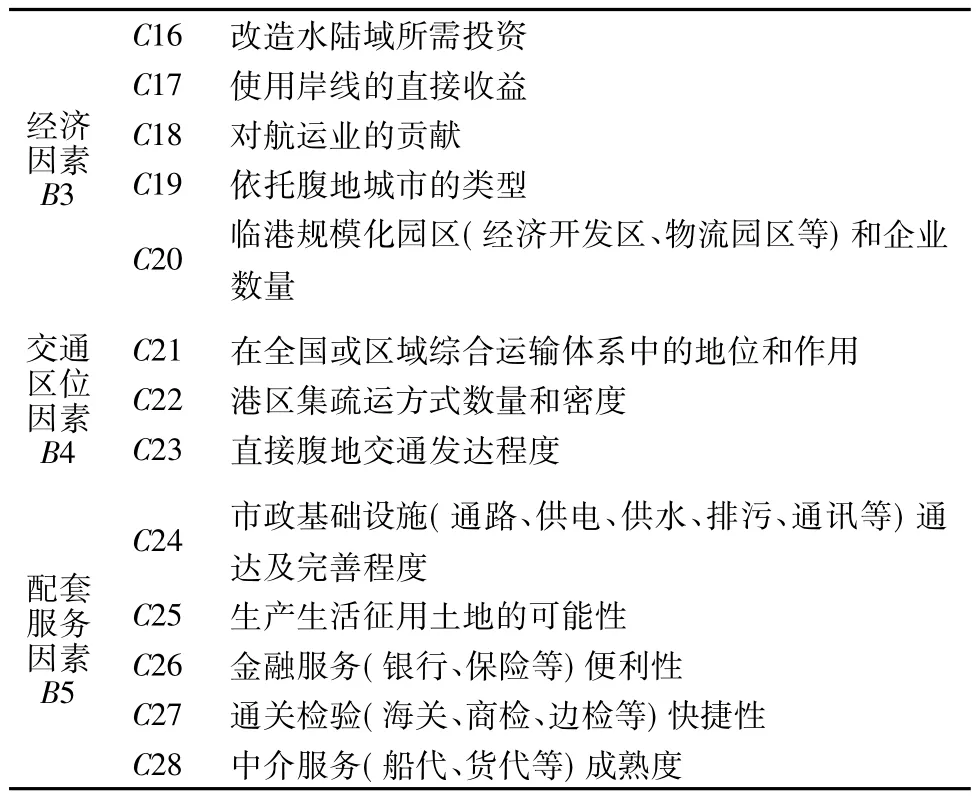
(续表1)

2 基于不确定性AHP和群决策理论的评价指标权重的确定

因为人们对事物认识的多样性以及评判过程中存在的不确定性和模糊性，所以，不确定性AHP法改变了传统AHP法中评估专家在构造判断矩阵时，比较的结果只能是介于1/9与9之间的1个确定数字的模式，而改由采用1个区间数来加以量化，这样就较好地解决了数值描述与实际状态不相符的问题。不确定性AHP法是对传统AHP法的改进，两者具有相同的应用步骤。不确定性AHP法评估指标权重的计算要分3步［5－6］:① 利用判断矩阵的一致性逼近与误差理论计算区间权重;②根据专家的打分结果，计算出各专家的相对可信度;③将各专家可信度和对指标的评判值加权汇总，得出最后各指标的权重。

2.1 区间权重计算［7－9］

2.1.1 区间数判断矩阵一致性逼近的计算

定理1:设某一区间判断矩阵A=(Aij)n×n，Aij=［aij，bij］，取则称M=(mij)n×n为满足互反性的一致性数字矩阵。

定理2:设A=(Aij)n×n为一致性数字判断矩阵，则A的权重向量为ω=(ω1，ω2，…，ωn) ，其中:

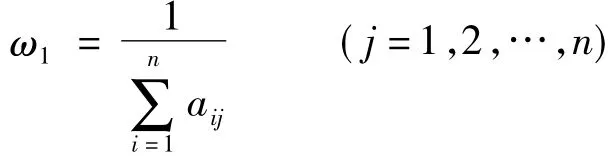
由定理1可知，令M的权重向量为ω=(ω1，ω2，…，ωn) ，其中:

2.1.2 误差传递理论在权重计算中的应用

将区间数判断矩阵A=(Aij)n×n，Aij=［aij，bij］，进行一致性逼近得判断矩阵M，其权重向量为ω=(ω1，ω2，…，ωn) 。记 ΔM1=(mij－aij)n×n，ΔM2=(bij－mij)n×n，ΔM1和 ΔM2称为A与M的极差矩阵。考虑随机误差的传递计算，设函数y=f(x1，x2，…，xn) ，x1，x2，…，xn的随机误差记为相应的均方差为 σx1，σx2，…，σxn，则函数y的随机误差均方差的计算公式为:

其中:ρij为相关系数。若xi的随机误差相互独立，则上面的公式可以简化为:

由于在大多数实际问题中，采用极差进行误差评定比较容易，因此函数y的随机误差传递公式可改写为:

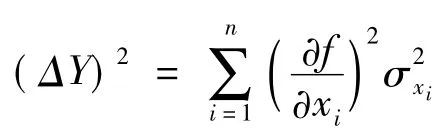
应用误差传递公式可进行区间数判断矩阵的权重向量分析计算。可得:

由极差矩阵定义知:

由此可得区间数判断矩阵A的权重为:

2.2 专家可信度的计算［10］

由于不同专家的知识背景不同，个人偏好不同，所以各专家评判值肯定有差异。为准确反应各个专家的评判水平，应求得各专家判断矩阵的可信度，并据此作为各专家的可信度。专家可信度由专家评判值的相似度和差异度来组合度量。

2.2.1 群判断中相似度的计算

利用向量间的空间位置关系来反映专家评判的相似性，即利用两向量夹角余弦的大小来反映。设有两个n维列向量α和β，其中α=(a1，a2，…，an)，β=(b1，b2，…，bn) ，两向量间的夹角为θ，则由两向量的夹角的余弦定义可知:

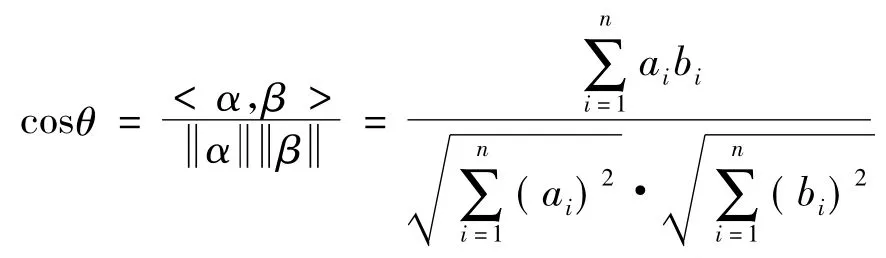
定义η=cosθ为两向量的几何相似系数，则0≤η≤1。

把特征向量转换为m个行向量α1，α2，…，αm，对应于m个专家所做的评判。令ηij表示αi与αj的夹角的余弦，即几何相似系数。令:

该式表示向量αi与其他向量的相似性之和，ηi越大，表示第i个专家的判断与其他专家的判断越接近，从而αi的可信度越高。把ηi归一化，即可得到用于描述第i个专家的判断与其他专家的判断相似程度大小的量μi:

2.2.2 群判断中差异度的计算

把特征向量转换为m个行向量α1，α2，…，αm，其中 αk=(ak1，ak2，…，akn) ，表示第k个专家对n个评判指标所作的评判值，设ei为各专家对第i个评判指标所作评判值的均值，则有:

表示第k个专家对每1个评判指标的评判值与对应指标评判值均值的差值总和。

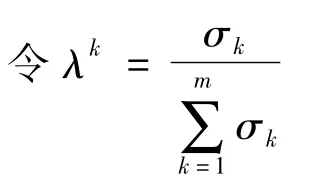
表示第k个专家的差值与所有专家的差值总和的比值，称之为第k个专家的差异度，其值越大，可信度就越低，反之越高。

2.2.3 群判断中可信度的计算

令ωk为第k个专家的可信度，当

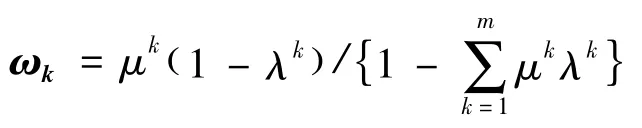
否则:ωk=μk

故可得到m个专家的可信度矩阵:

2.3 判断因素(评价指标)相对权重的计算

αk=(ak1，ak2，…，akn) ，表示第k个专家对n个评判因素所作的评判值(即判断矩阵的特征向量)，ω'k=(ω'1，ω'2，…，ω'k，…，ω'm) ，表示m个专家的可信度矩阵。则第i个判断因素的相对权重为:

3 评价指标定量化

港口岸线等级评价指标定量化是件很复杂的事情，部分指标可以直接定量化，如气候条件中年雾日或其他恶劣天气导致码头不能作业的天数、改造水陆域条件所需投资额、使用岸线的直接收益等，只需要按水工工程设计技术规范或按常理确定一个满意值(上限)和不满意值(下限)，根据实际值按上限(1)和下限(0)插值即可。具体插值方法为:

式中:Wki为第k段港口岸线第i个评价指标的定量化评分(0＜Wki＜1);Pk定i为第k段港口岸线第i个评价指标的直接定量化值;P上i为港口岸线第i个评价指标的满意值上限;P下i为港口岸线第i个评价指标的满意值下限。其余大部分指标属定性指标，不能直接定量描述，可采用专家打分法来使其定量化，即设定满意值(上限)为1，不满意值(下限)为0。另外，定性指标除很满意(上限)为1，不满意(下限)为0外，还约定中间取值的参考标准:满意为0.9，比较满意为 0.7，一般为 0.5，较不满意为 0.3。

4 评价结果的计算与归类

式中:Sk为第k段港口岸线的综合得分值，0＜Sk＜1;Zi为港口岸线第i个评价指标的总权重，0＜Zi＜1;Wki为第k段港口岸线第i个评价指标的定量化得分，0＜Wki＜1。

结合以往研究成果和相关专家的意见，最终评价结果可以归类为3个不同的等级。即:一类港口岸线(0.85≤Sk≤1);二类港口岸线(0.70＜Sk＜0.85);三类港口岸线(0.60≤Sk≤0.70)。此外，若Sk＜0.6，则说明该岸线有明显的先天不足，要建设成为港口岸线，需要经过很复杂很困难的工程整治，技术上和经济上都很不合理，因此不适合作为港口岸线，可在经过有关主管部门的批准后调剂到相关行业开发利用或直接留作自然岸线保存。

港口岸线等级评价模型的计算公式为:

5 算例分析

现有5位权威专家进行评判打分，以第1级指标为例，5位专家的评判数据为:

5.1 计算区间权重

根据区间权重计算公式，可得表2所示的各专家对1级评判指标的评判值区间。

表2 各专家对1级评判指标的评判值区间汇总Tab.2 Summary of the first level indicator value by experts

5.2 计算专家可信度

将表2中各专家对1级指标的评判值区间取中值，作为各专家对1级指标的评判值，并组成5个行向量，即:

则有:各专家与其他专家评判相似度为:

μ1=0.200 0;μ2=0.200 0;μ3=0.200 0; μ4=0.199 9; μ5=0.200 1

则有:各专家的评判差异度为:λ1=0.236 3;λ2=0.130 7; λ3=0.199 7; λ4=0.322 6; λ5=0.110 7

表3 1级指标最终评判结果Tab.3 The final evaluation results of the first level indicators

同理，各2级指标权重的评判结果也可依此算出。

5.3 计算各评价指标的总权重

将指标层中每个指标的相对权重乘以与之对应的某类因素的权重，计算结果见表4。

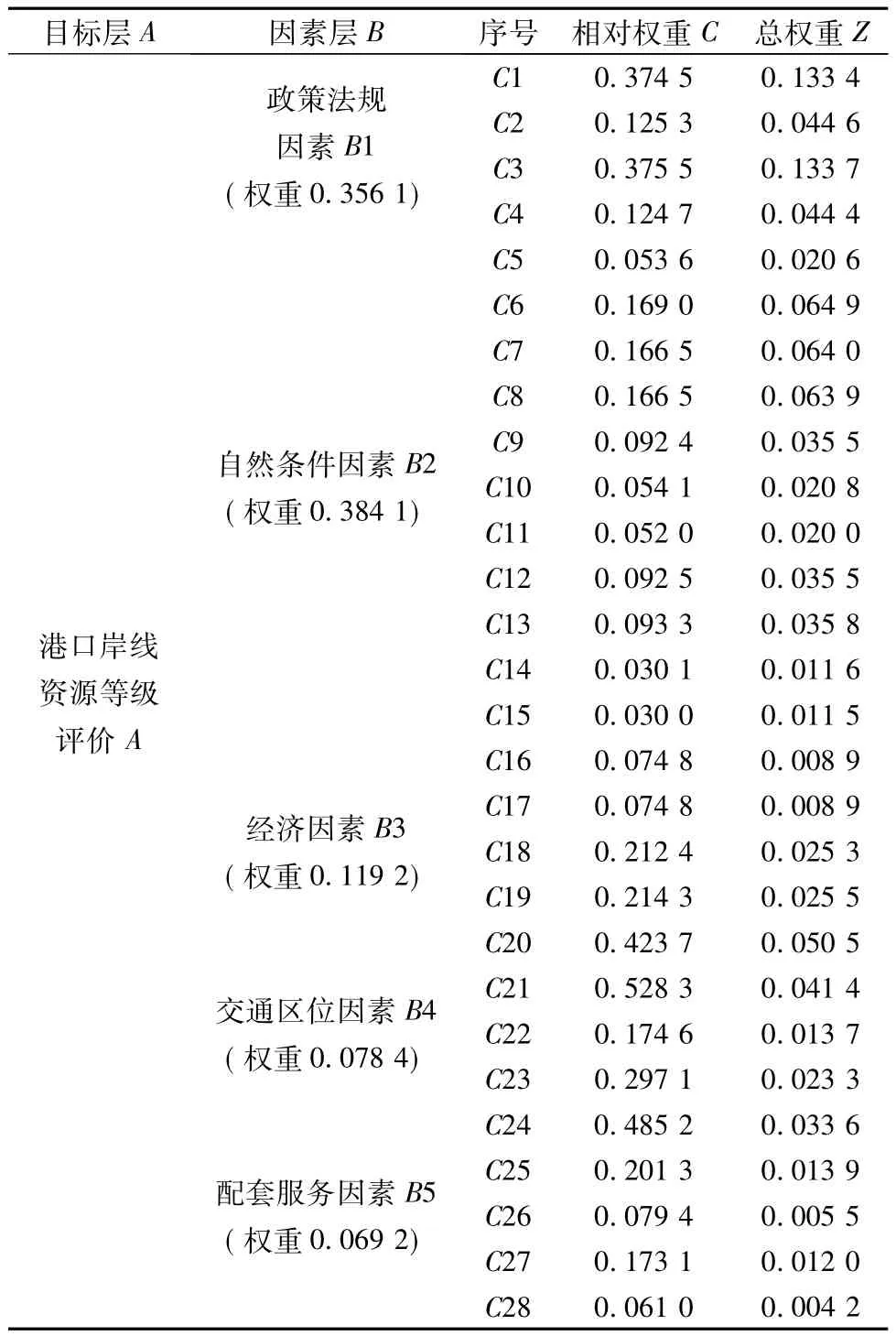
表4 各指标总权重汇总Tab.4 Summary of the total weight of each index

5.4 实证分析

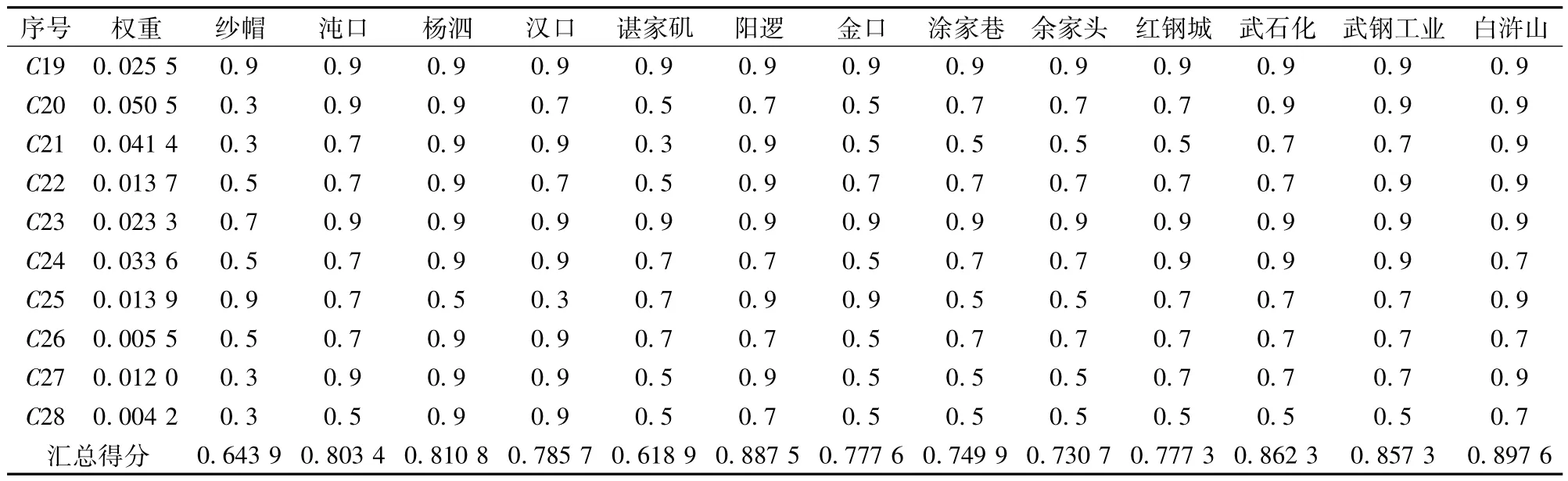
以长江武汉段已建的17个港区为例，将专家的评判数据输入并计算，结果见表5。

根据以上计算结果，可以将13个评价港区单元划分为3类。即:

一类港口岸线(0.85≤Sk≤1):白浒山港区岸线(Sk=0.897 6)、阳逻港区岸线(Sk=0.887 5)、武石化港区岸线(Sk=0.862 3)、武钢工业港港区岸线(Sk=0.857 3)。一类港口岸线是建设港口码头，特别是公用码头的优良岸线，没有自然岸线资源方面的明显缺陷，具有强烈的排他性。应确保用于港口建设，并在码头建设集约化和运营高效率的原则下合理使用、持续开发。

二类港口岸线(0.70＜Sk＜0.85):杨泗港区岸线(Sk=0.810 8)、沌口港区岸线(Sk=0.803 4)、汉口客运港区岸线(Sk=0.785 7)、金口港区岸线(Sk=0.777 6)、红钢城港区岸线(Sk=0.777 3)、涂家巷港区岸线(Sk=0.749 9)、余家头港区岸线(Sk=0.730 3)。二类港口岸线，是建设港口比较优良的岸线，有一定的自然条件方面的不足，但也具有较强的排他性。应优先用于港口建设，遵循深水深用、浅水浅用、远近结合、各得其所的原则加以开发利用。

三类港口岸线(0.60≤Sk≤0.70):纱帽港区岸线(Sk=0.643 9)、谌家矶港区岸线(Sk=0.618 9)。三类港口岸线，是经过一定的工程措施整治后可以建设港口的岸线，虽有明显的先天不足，但也具有一定的排他性。在港口岸线资源充裕的前提下，经过所在地交通主管部门同意，可以允许调剂到相关行业开发利用。

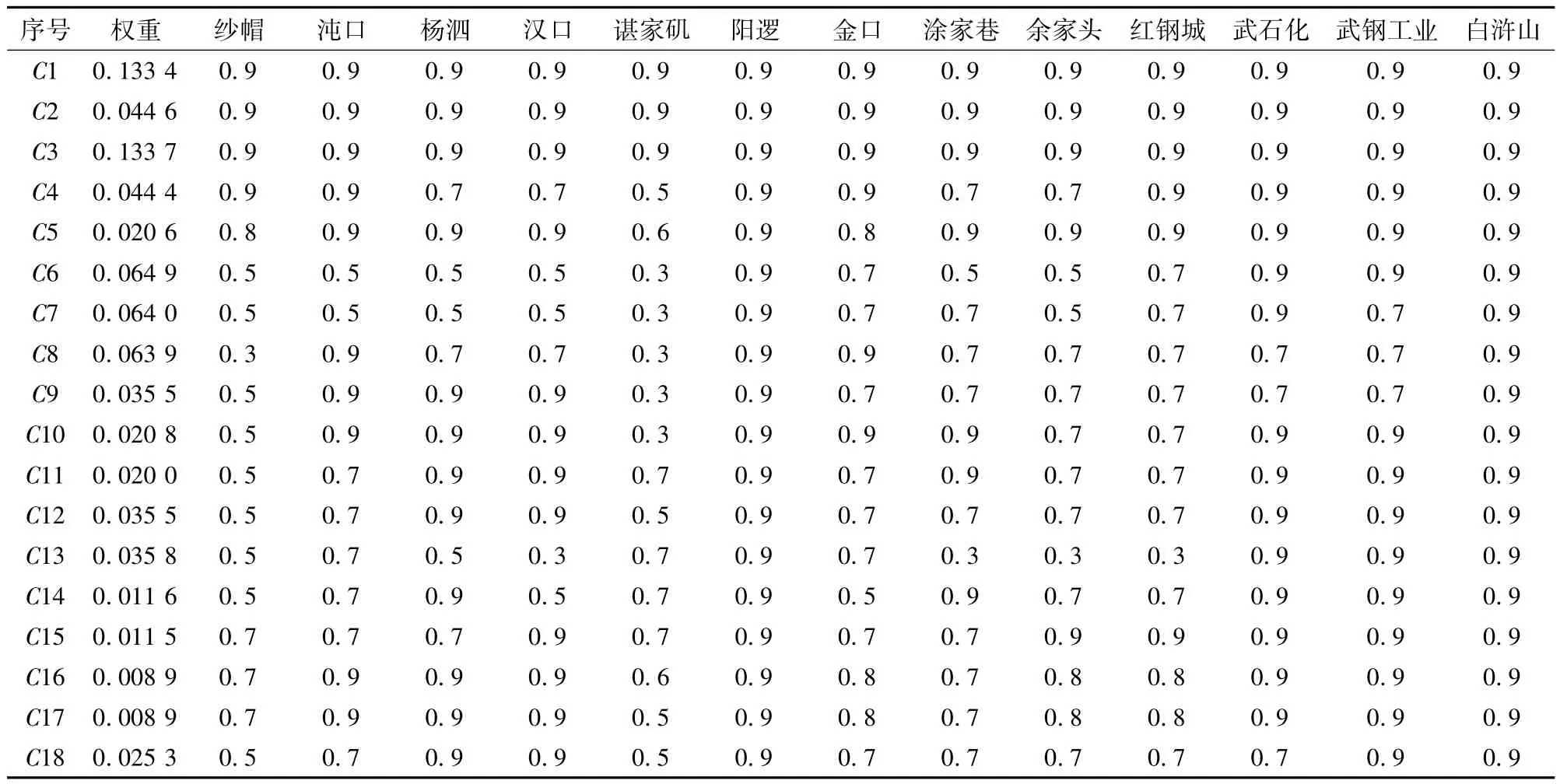
表5 各评价单元得分汇总Tab.5 Summary of the score of each evaluation unit

(续表5)

6 结语

笔者在全面梳理影响港口岸线等级优劣因素的基础上，确定了评价指标体系。在计算指标权重时，引入了不确定性AHP法和群决策理论，使评价计算结果更具可信性。实证表明，该方法克服了原有评价方法的弊端，提高了评价结果的准确性和科学性，具有较好的实践运用价值。

［1］杨大鸣，王呈芳，张培林.港口岸线评价模型及其应用［J］.水运工程，2003，351(4):38 －42.

［2］马荣华，杨桂山，陈雯.长江江苏段岸线资源评价因子的定量分析与综合评价［J］.自然资源学报，2004，19(2):176 －182.

［3］许光委.港口岸线的资源性分析和等级评价研究［D］.天津:天津大学，2005.

［4］邱彬皇.港口岸线资源评价与适应性研究［D］.上海:上海海事大学，2007.

［5］王莲芬.层次分析法引论［M］.北京:中国人民大学出版社，1990.

［6］唐秋生，张洋，李萍.基于层次分析与灰关联分析的公路货运市场细分方法［J］.重庆交通大学学报:自然科学版，2008，27(2):313－316.

［7］刘进生，魏毅强，王绪柱.区间数判断矩阵的建立及其评分权重计算［J］.系统工程，1993，11(3):43 －45.

［8］董元帅，唐伯明.基于区间数法的水泥路面使用性能评价［J］.重庆交通大学学报:自然科学版，2009，28(5):870－872.

［9］许先云，杨永清.不确定AHP判断矩阵的一致性逼近与排序方法［J］.系统工程理论与实践，1998(2):19－22.

［10］秦学志，王雪华，杨德礼.AHP中群组判断的可信度法［J］.系统工程理论与实践，2000，19(5):76－78.