瓦斯发动机燃气混合器瓦斯阀口流量特性分析与结构优化

郎 华，高 松，谭德荣，邵金菊

(山东理工大学交通与车辆工程学院，山东淄博255049)

瓦斯是煤矿采煤过程中伴生的一种高热值可燃清洁能源，其温室效应危害程度是CO2的21倍，瓦斯的开发和利用具有巨大的潜在经济效益和环境效益。目前，通过发电技术将瓦斯转化为电能已成为一种应用较为广泛且较为经济的开发利用途径［1－2］。而瓦斯发动机是瓦斯发电机组的核心组成部分，当瓦斯发动机工况及瓦斯气源浓度、压力发生变化时，瓦斯发动机空燃比就会随之发生变化并偏离理想空燃比，从而导致发动机运行不稳定甚至熄火［2］。为此，瓦斯发动机空燃比控制系统通过调节燃气混合器瓦斯阀口开度来使发动机维持在理想空燃比。但是，圆形和长方形燃气混合器瓦斯阀口的流量与其开度(阀口面积)往往呈非线性关系，这将直接影响到空燃比控制时的实时性和准确性。

笔者在分析长方形燃气混合器瓦斯阀口流量特性的基础上，设计了流量与其开度呈准线性关系的燃气混合器瓦斯阀口型线，有效地消除了空燃比调节时产生的时滞影响，提高了瓦斯发动机空燃比控制的实时性和准确性，为发电机组的正常运行提供了保证。

1 长方形瓦斯阀口流量特性建模与分析

图1为某瓦斯发动机燃气混合器截面简图，该混合器瓦斯阀口为长方形结构，且均布于混合器内腔腔体一周。当瓦斯经供给管道进入混合器后，从瓦斯阀口进入混合器内腔，与前端经引射进入的空气混合后形成均匀可燃燃气，瓦斯阀口开度通过与控制杆相连的控制活塞进行调节。

在混合器瓦斯供给管道接口截面和混合器瓦斯阀口截面之间，列总伯努利方程如式(1):

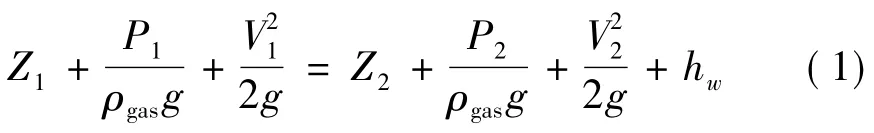
式中:Z1、Z2分别为两截面处的位置水头，m;P1、P2分别为两截面处的气体压强，Pa;V1为瓦斯供给管道接口截面处瓦斯流速，m/s;V2为瓦斯阀口处瓦斯流速，m/s;hw为瓦斯流经瓦斯阀口时的局部能量损失，J。

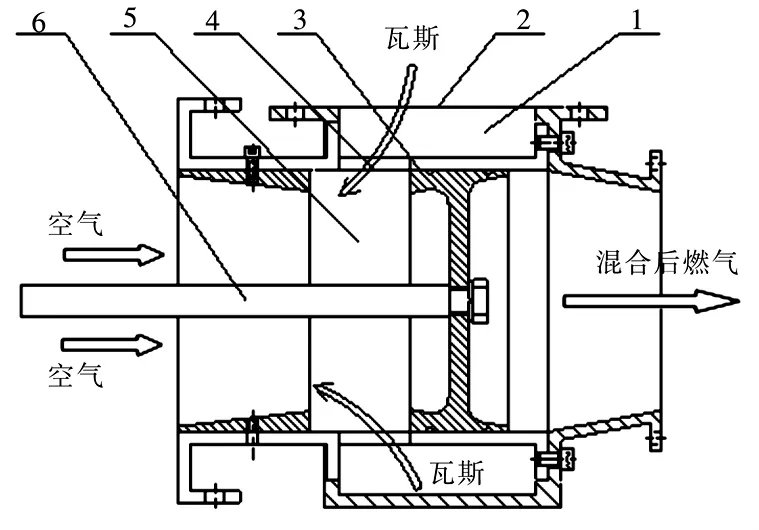
图1 燃气混合器截面简图Fig.1 Cross-section diagram of gas mixer

由于该过程瓦斯流程较短，故沿程能量损失可忽略不计，只须考虑瓦斯流经瓦斯阀口时产生的局部能量损失hj［3］，即:

式中:ξ为局部损失系数，无量纲。

而局部损失系数又与节流孔流速因数有关，并与流速因数φ平方成反比［4］，如式(3):

由气体连续性方程，并将式(2)、式(3)代入式(1)可整理得如下速度关系:

式(4)中:P2可参照总伯努利方程及气体连续方程［5］，并依据气体在文丘里管结构中的运动特性求得。

图2是混合器内部文丘里管结构示意简图，其中文丘里管空气入口和混合燃气出口直径为160 mm，喉口直径为140 mm，喉部长度为81 mm。经推导，P2可表示为:

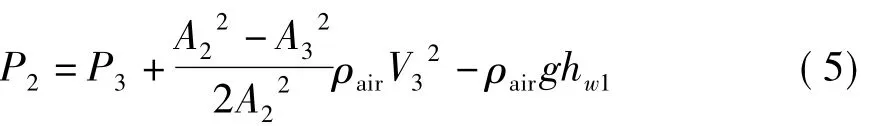
式中:V3、A3分别为文丘里管空气入口截面处空气流速和截面积，m/s，m2;A2为文丘里管中间截面处截面积，m2;hw1为空气流经文丘里管产生的能量损失，J。

为简化公式，可令:

M1/A12，A2=S，N=1/φ2。其中S为混合器内腔瓦斯阀口截面积，则式(4)可简化整理为如下关系:

式中:V(S)为混合器瓦斯阀口瓦斯流速函数。

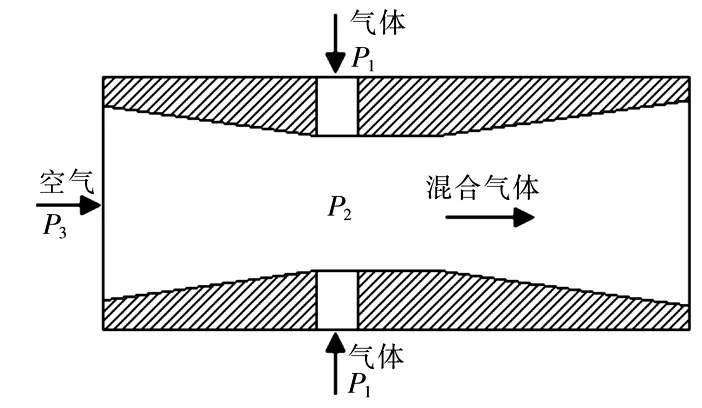
图2 混合器内部文丘里管结构示意Fig.2 Schematic diagram of internal Venturi tube in gas mixer

结合当量直径转换后，混合器方形瓦斯阀口任意开度时的瓦斯流量数学模型可表示为如下关系:

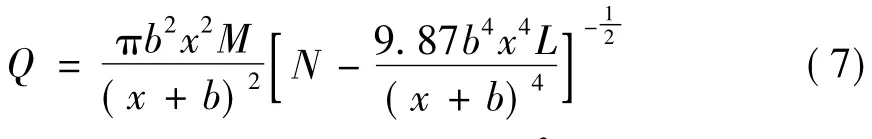
式中:Q为燃气进口瓦斯流量，m3/s;x为瓦斯阀口开度，m;b为方形瓦斯阀口宽度，m。

由式(7)可知，方形瓦斯阀口流量Q与其开度x呈非线性关系。为进一步对其验证，采用计算流体力学Fluent软件进行仿真。根据瓦斯发动机和瓦斯供给管道参数，结合式(7)中各参数的定义形式，设定如下:M=93.7，N=1.06，L=44，b=0.02。仿真时首先通过Gambit软件对绘制的方形瓦斯阀口燃气混合器三维结构图进行预处理，生成网格文件之后再导入 Fluent－3D 求解器［6－7］，仿真计算时混合器基本边界条件设置如下:混合器空气进口压力P3=101 kPa，混合器瓦斯进口压力P1=96 kPa。

图3是根据仿真所得瓦斯阀口平均流量与其对应的阀口开度数据，拟合得到的方形瓦斯阀口单一进口流量与开度的关系曲线。

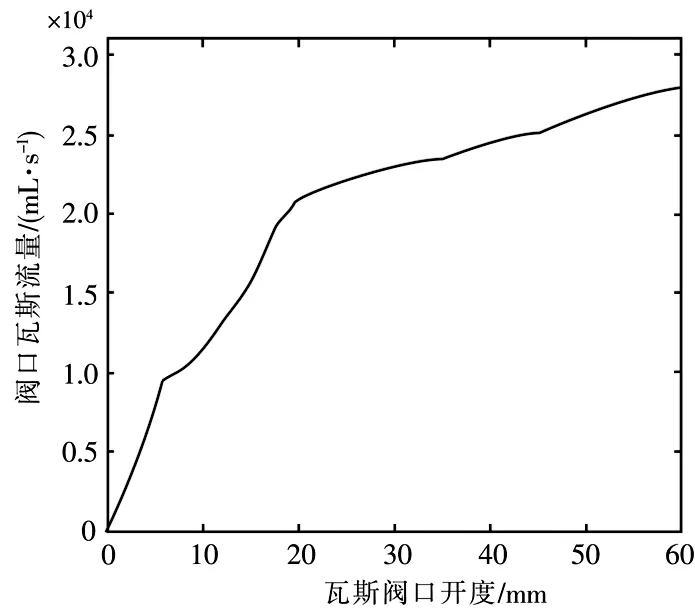
图3 方形瓦斯阀口流量特性曲线Fig.3 Flow characteristics curve of rectangular gas valve port

从图3中可看出，燃气混合器瓦斯阀口流量与其开度呈非线性关系，虽然当阀口开度大于18 mm时线性度较好，但该混合器仍然不能满足线性控制要求。因此，必须对燃气混合器阀口型线进行优化设计。

2 准线性流量特性阀口型线设计

通过应用流体力学原理分析发现，出现上述现象的原因主要在于瓦斯阀口开度较小和开度相对较大时应用了相同的瓦斯流动模型。分析表明:当瓦斯阀口开度较小时，其流动过程等同于流体流经缝隙的流动过程;阀口开度较大时，流动模型等同于流体流经节流口时的流动模型。所以可考虑采用“分段、分模型”设计思想进行阀口型线优化设计。

2.1 瓦斯阀口小开度型线设计

混合器瓦斯阀口处于小开度时，控制活塞与瓦斯阀口边缘之间形成了一个缝隙。瓦斯流过该缝隙的过程，可根据流体在两平行平板缝隙间流动的模型理论处理［8］，瓦斯平均速度可表示为:

式中:μ为瓦斯的动力黏度，Pa·s;l为混合器进口厚度，m;x为混合器瓦斯阀口开度，m;Δp为混合器内外腔压差，Pa。

此时阀口瓦斯平均流量可表示为如下关系:

式中:S为瓦斯阀口开启面积，m2。

若使瓦斯流量与阀口开度成线性关系，则由式(9)求得的关于x的一阶导数应为常数，即:

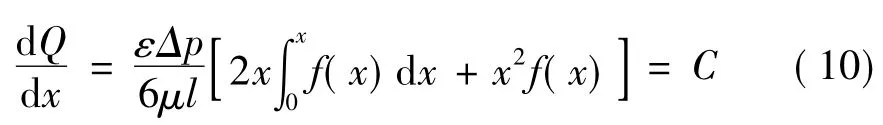
式中:C为常数;f(x)为阀口上下边缘曲线函数。对式(10)求关于x的二阶导数可得如下关系:

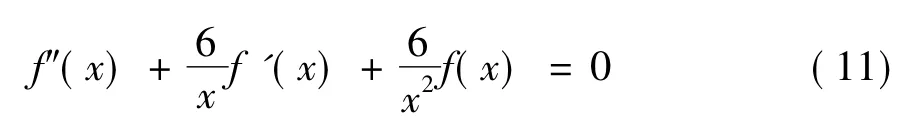
经上述处理之后，f(x)的求解过程最终转化为了二阶变系数齐次线性微分方程求解的问题，经求解方法所求f(x)的解析式如下［9］:

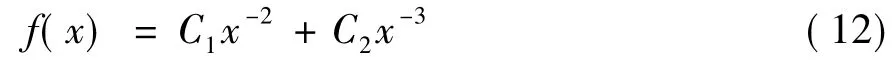
式中:C1、C2为非0常系数。

2.2 瓦斯阀口大开度型线设计

结合长方形瓦斯阀口流量模型推导过程，瓦斯阀口大开度时瓦斯流量模型可表示为:

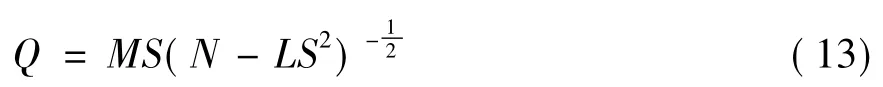
若使混合器瓦斯阀口流量与阀口开度呈线性关系，则阀口瓦斯进气量增益K须为常数，即:

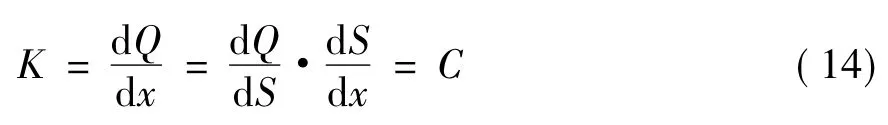
式中:C为常数。

为简化处理，式(14)中瓦斯进气量增益K可分解为KQS=dQ/dS和KSx=dS/dx两部分，其中KQS为瓦斯阀口开启面积相对燃气进气量的增益;KSx为非线性瓦斯进口的面积增益，即进气口开度变化所引起的面积增益。

将式(13)两边同时对S求导得如下关系:

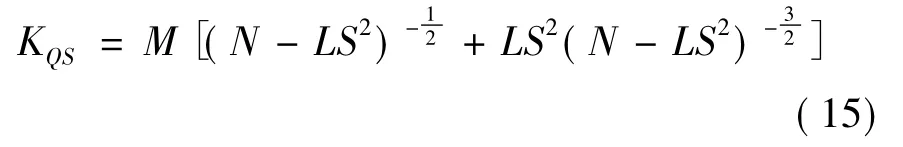
将式(15)代入式(14)整理得:

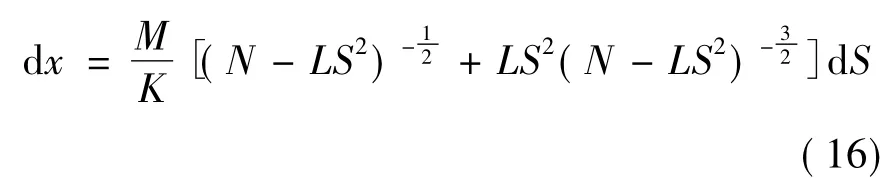
由式(16)可得S关于x的如下函数关系式:

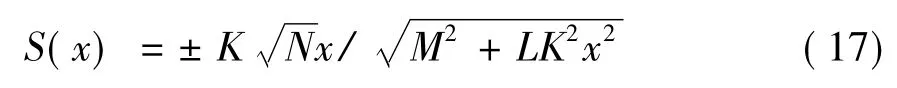
将式(17)对x求导即可得到混合器瓦斯阀口边缘函数关系，如式(18):

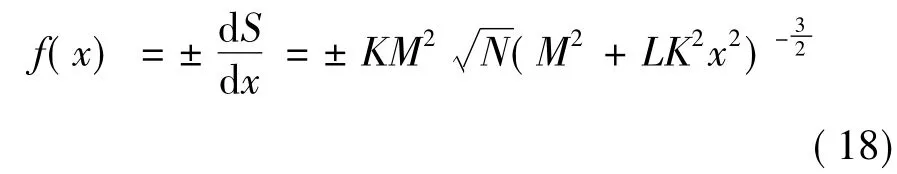
优化后的准线性混合器瓦斯阀口型线设计公式可表示为:

式中:t为上下两曲线交点的横坐标值;其他参数依瓦斯发动机、瓦斯供给管道及瓦斯气体参数而定。

3 瓦斯阀口流量特性仿真

仿真之前首先根据阀口型线设计公式(19)绘制优化后的燃气混合器三维结构图，型线设计时式(19)中各系数设置如下:

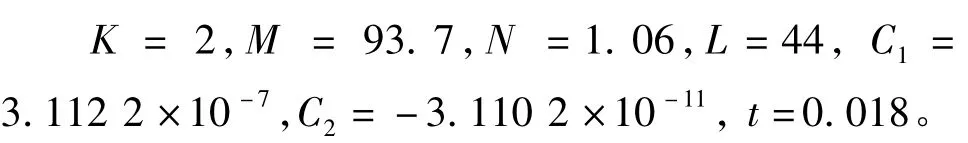
燃气混合器三维结构图绘制完成后通过导入前处理软件Gambit生成网格文件，最后再利用Fluent－3D求解器进行仿真实验［6－7］。仿真时混合器空气进口压力和瓦斯进口压力边界条件分别设置为101 kPa和96 kPa。

图4为根据Fluent仿真实验数据拟合得到的瓦斯阀口单一进口流量与开度的关系曲线。从曲线中可看出，优化后的瓦斯阀口流量与开度曲线跟优化前相比线性度较好，瓦斯流量变化连续平稳，阀口瓦斯流量与其开度呈准线性关系，阀口流量特性得到了进一步优化，达到了优化设计目标和控制的要求。

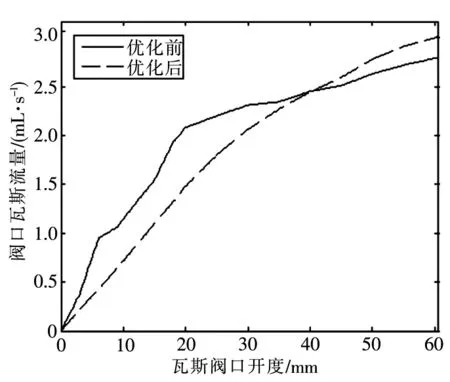
图4 优化前后瓦斯阀口流量特性曲线对比Fig.4 Comparison of flow characteristics curves before and after optimization

4 结论

对方形瓦斯阀口流量特性建模分析表明:方形阀口瓦斯流量与其开度呈非线性关系。因此，原瓦斯发动机所用燃气混合器不具备线性控制的条件，空燃比控制过程势必导致控制响应滞后，控制系统难以达到稳定。通过运用流体力学原理分析，确定了燃气混合器瓦斯阀口小开度和大开度时的流动模型，采用“分段”“分模型”思想设计出了准线性瓦斯阀口型线。仿真结果表明，优化后的瓦斯阀口流量与其开度近似呈线性关系，且线性度良好，可以满足线性控制要求，达到了优化设计目标，为瓦斯电站的正常平稳运行提供了可靠保证。

［1］尹娟，翁一武，SU Shi.煤矿通风瓦斯在燃气轮机中的催化燃烧特性［J］.动力工程，2009，29(2):104 －105.

［2］李光举.燃气发动机空燃比控制系统研究与开发［D］.淄博:山东理工大学，2008.

［3］王松龄.流体力学［M］.北京:中国电力出版社，2004:94－95.

［4］孟凡英.流体力学与流体机械［M］.北京:煤炭工业出版社，2006:95－97.

［5］张道文.混合器优化设计［J］.汽车技术，2003(7):11－12.

［6］韩占忠，王敬，兰小平.FLUENT:流体工程仿真计算实例与应用［M］.北京:北京理工大学出版社，2004:218－227.

［7］李新森，张建卓，毛君，等.基于FLUENT的大流量安全阀流场数值模拟［J］.煤矿机械，2009，30(8):45 －46.

［8］曾贤启.工程流体力学基础［M］.北京:航空工业出版社，1993:94－97.

［9］李鸿祥.两类二阶变系数微分方程的求解［J］.高等数学研究，2002，5(2):10－11.