Ni[N(CN)2]2的电子结构的第一性原理研究

俎凤霞,刘敏敏

(武汉工程大学理学院,湖北武汉 430074)

Ni[N(CN)2]2的电子结构的第一性原理研究

俎凤霞,刘敏敏

(武汉工程大学理学院,湖北武汉 430074)

运用密度泛函理论(DFT)并采用全势线性缀加平面波(FPLAPW)方法对分子磁体Ni[N(CN)2]2的电子结构和磁性质进行了计算.通过总能量、态密度以及自旋磁矩分布系统地研究了体系基态的相对稳定性和电子结构.结果表明,基态的Ni[N(CN)2]2是一个分子基铁磁半导体.基态的态密度计算给出了磁性的主要来源是分子中的Ni成分.

态密度;电子结构;铁磁耦合

0 引 言

通常铁磁性材料大多为含有3d和4f轨道的金属、合金和矿物等无机材料[1],而有机分子大多由于具有闭合壳层的电子构型而呈抗磁性.由于无机铁磁性材料的应用常常受到种类和加工方法的限制,无法满足科学技术的飞速发展对磁性材料提出的越来越高的要求[2-3].从20世纪60年代初期,科学家们就开始了对分子铁磁体的理论研究,但直到20世纪80年代后期才开始分子铁磁体的实验研究[4].世界各国的科学家经过多年的共同努力,迄今已合成几十个宏观分子铁磁体.分子磁性材料的磁性有其本身的特点,因而决定了它特殊的应用前景.这种材料的磁性是表现在分子水平上,又可通过化学合成而控制其结构,因此很有希望用作磁存储单元,极大地提高存储密度[5].

近十年来,二价过渡金属双氰胺作为分子基铁磁体已经引起了人们的普遍关注,这类化合物主要是由过渡金属(Mn,Fe,Co,Ni和Cu)离子和有机双氰胺配体[N(CN)2]2组成[6].近来实验方面已经合成制备出了Cu,Ni,Co,Fe和Mn基材料,而后Kmety等人报道了这类家族的分子基磁体有两个成员的基态是铁磁的[7-8].本文运用全电子势线性缀加平面波方法计算了Ni[N(CN)2]2的电子结构和磁性质,以便深入理解它内部的铁磁相互作用机制.我们得到了体系的总能量、态密度和自旋分布.电子退局域化与自旋极化的相互竞争很好地解释了原子的自旋分布.本文结果对这类体系的强铁磁性的起源问题提供新的洞察力,可为设计新的有机铁磁材料提供理论指导.

1 理论方法

笔者运用基于密度泛函理论(DFT)的全电子势线性缀加平面波(FLAPW)法对掺杂的有机材料Ni[N(CN)2]2进行了第一性原理计算.对于非磁性材料的基态构型,电子态乃至声子态的研究,许多第一性原理计算,如赝势平面波(PW)法[9]、线性 muffin-tin轨道(LMTO-ASA)法、变分法(DVM)、全电子势线性缀加平面波(FLAPW)法等,已普遍被采用,在理解材料的性能方面,提供了很有价值的理论指导[10-11],而磁性材料多了自旋自由度,一般采用自旋局域密度近似(LSDA),这对第一性原理计算提出了更高的和更复杂的要求:在研究磁性结构时,芯电子的贡献(特别是有机分子中内壳层缺乏p轨道)往往显得较为重要,冻结芯电子的PW法在这方面的处理显得较为粗糙,而LMTO-ASA和DVM只是在处理含有d轨道的过渡金属的磁性问题时,才显得较为有利,对有机高分子的磁性研究,用FLAPW法是一条较为精确和切实可行的研究途径.我们采用的Wien97软件包做了具体的数值计算[12],考虑到在有机化合物中电荷密度的变化可能很大,笔者采用广义梯度近似(GGA)[13],这种近似方法已被具体的计算表明是适合有机磁体的[14-15].

2 结果与讨论

2.1 体系的基态

化合物Ni[N(CN)2]2的每个单位原胞包含两个分子单元,金属离子位于原胞中 (0,0,0)和(1/2,1/2,1/2)处,其中每个金属离子周围是一个拉长的八面体NiN6,有关的Ni[N(CN)2]2晶体的结晶学数据在 Kmety等人的实验中给出[6],我们在计算的过程中直接使用了这些数据.

Kemty等人的实验测定了Ni[N(CN)2]2具有铁磁基态[7],但至今未有理论方面的证实,鉴于此,运用Wien2k程序对化合物Ni[N(CN)2]2执行了自洽的电子带结构计算,通过计算该体系的总能量来确定它的基态,分别得出了铁磁态(FM),反铁磁态 (AFM)和无磁相互作用 (NM)三个状态的总能量,结果见于表1.显然铁磁相的能量是三个中最低的,说明铁磁相是最稳定的,因此确定了铁磁态是体系的基态.且具有3.873的净磁矩.下面的工作都是就铁磁相的Ni[N(CN)2]2来展开研究.

表1 铁磁相(FM),反铁磁相(AFM)和无磁相(NM)的总能量和磁矩Table 1 The total energy and magnetic moments of the ferromagnetic(FM),antiferromagnetic(AFM) and non-magnetic(NM)phases

2.2 体系的态密度

为了调查不同交换关联势对体系的带结构和磁特性的影响,选择了两种交换关联势 GGA和LDA来系统地计算了基态下Ni[N(CN)2]2电子结构.图1给出了在这两种不同的交换关联势下体系的总的态密度.

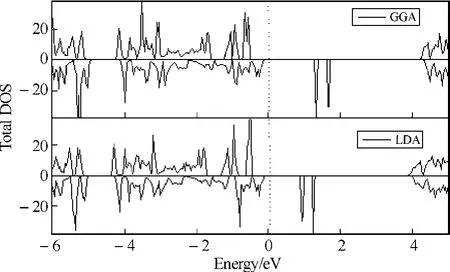
图1 Ni[N(CN)2]2在两种不同的交换关联势GGA和LDA下的总态密度Fig.1 The total density of states within the two different exchange-correlation potential GGA and LDA

从图1中,可以发现总态密度分布似乎大致相同,即在费米能级附近,自旋向上和向下的电子态密度分布明显地劈裂,且同一能带分裂成的两个子能带,自旋下的能带在费米能级上方,自旋向上的能带在费米能级的下方.这表明这一体系中,由于未配对电子的存在,有序电子自旋排列在电子交换和关联的作用下有条件地出现了,证实了基态的Ni[N(CN)2]2是一个铁磁有序结构.然而,这两种态密度分布曲线的一个明显的区别就是带间距的不同,在 GGA势中的带间距(1.333 7 eV)要比采用 LDA 时的间距(0.925 2 eV)大一些,这就是常见的 GGA带间距效应[13].

2.3 体系的自旋磁矩

为了定量讨论体系中的各原子对磁性的贡献,我们计算了自旋磁矩.表2的前两列给出了在GGA和LDA交换关联势下各原子的自旋磁矩以及单位原胞的总磁矩.可以看出,与LDA的结果相比,在GGA势下得出的磁矩要高一些.对于那些包含弱键或氢键的体系(比如分子晶体),GGA应该是更有效的,因为对于这些系统,在LDA中分子间的键长被严重地低估了,而在GGA中有明显的提高.

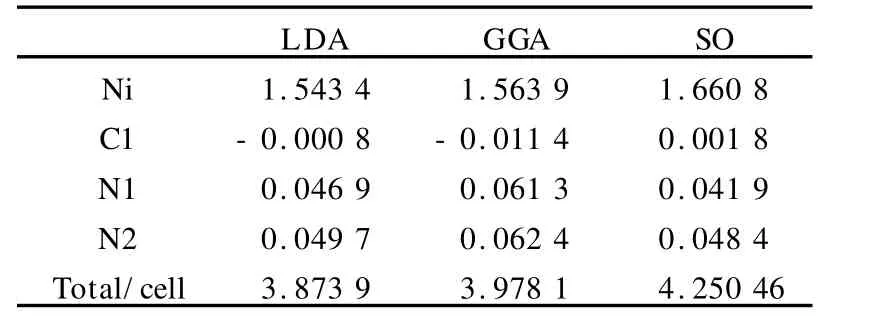
表2 体系中各原子的自旋磁矩分布Table 2 The spin magnetic moment populations for the title compound μB

通过表2还可以发现,Ni原子的自旋磁矩要比别的原子的大得多,这些定量的数据揭示了体系的磁性主要来源于铁磁性的Ni原子而其他原子的贡献较小,这主要是由于提供磁矩的未成对电子大部分来源于过渡金属Ni原子.从表2也可得知,本来不具有未成对电子的有机配体阴离子中的C1、N1和N2原子也显示出了部分自旋磁矩.这意味着Ni d轨道和N1、N2原子的p轨道存在有杂化现象,这样净自旋磁矩就会出现在有机配体中的N1和N2原子上.而在C1位置上的小的负的自旋磁矩揭示了在这个有机配体内自旋极化起主要作用.此外,我们看到无论是采用GGA还是LDA交换关联势,计算结果都表明Ni位置的磁矩与 Kmety等人的实验值(μ=2.21μB)相比要的低一些[7].因此,为了进一步探讨这是否与自旋轨道相互作用的贡献有关,我们计入了自旋-轨道耦合(SO),Kemty等发现这个化合物铁磁有序的易磁化轴沿着a(x)方向[7],与此对应,在计算过程中我们也选择自旋方向沿着[001]方向,各原子磁矩的结果也被列入表2的第三列,正如所预料的,自旋轨道耦合的包括对Ni原子的磁矩有所提高,同时我们获得Ni 3d轨道磁矩0.124 1μB.

最后,值得注意的是,如图1所示,无论是GGA还是LDA作为交换关联势都发现基态的Ni[N(CN)2]2是一个分子基铁磁半导体,如果这一结果被实验进一步证实,将为半导体领域的新一代电子器件提供有价值的材料.

3 结 语

采用精确的第一性原理方法计算了Ni[N(CN)2]2的电子结构和磁性质,以便深入理解它内部的铁磁相互作用机制,通过总能量计算表明基态的Ni[N(CN)2]2是一个分子基铁磁半导体.为了调查不同交换关联势对体系的带结构和磁特性的影响,选择了两种交换关联势GGA和LDA来系统地计算了基态下Ni[N(CN)2]2态密度及自旋磁矩分布.态密度和自旋密度分布都揭示了磁性主要来源于Ni原子而其他原子的贡献较小,这主要是由于提供磁矩的未成对电子大部分来源于过渡金属Ni原子.

[1] 戴道生,钱昆明.铁磁学[M].北京:科学出版社, 1987.

[2] Gatteschi D,CarrettaP,Lascialfari A.Molecular magnets and magnetic nanoparticles: new opportunities forμSR investigations[J].Physica B: Condensed Matter,2000,289:94-105.

[3] Joel S Miller.Organometallic-and Organic-Based Magnets:New Chemistry and New Materials for the New Millennium[J].Inorg Chem,2000,39(20): 4392-4408.

[4] Korshak Yu V,Medvedeva T V,Ovchinnikov A A,et al.Organic polymer ferromagnet[J].Nature,1987, 326:370-372.

[5] Tatiana L Makarova,Bertil Sundqvist,Roland Höhne,et al.Magnetic carbon[J].Nature,2001,413: 716-718.

[6] Jamie L Manson,CarmenR Kmety,Qing-zhen Huang,et al.Structure and magnetic ordering of M[N(CN)2]2(M=Co,Ni)[J].Chem Mater,1998, 10(9):2552-2560.

[7] CarmenR Kmety,Jamie L Manson,Qingzhen Huang,et al.Collinear ferromagnetism and spin orientation in the molecule-based magnets M[N(CN)2]2(M=Co,Ni)[J].Phys Rev B,1999, 60(1):60-63.

[8] Carmen R Kmety,QingzhenHuang,Jeffrey W Lynn,et al.Noncollinear antiferromagnetic structure of the molecule-based magnet Mn[N(CN)2]2[J]. Phys Rev B,2000,62(9):5576-5588.

[9] 徐金荣,王影.聚苯并噻吩电子结构的第一性原理研究[J].山东理工大学学报:自然科学版,2009,23 (6):11-13.

[10] 刘芳,王茺,李亮,等.利用第一性原理研究 Ge:Si电子结构与光学性质[J].材料导报,2009,23(14): 75-79.

[11] 秦芳,王茺,邓荣斌,等.Si(001)面弛豫表面构型与电子结构的第一性原理[J].粉末冶金材料科学与工程,2009,14(3):143-146.

[12] Blaha P,Schwarz K,Sorantin P,et al.Full-potential linearized augmented plane waveprograms for cnystalline systems[J].ComputPhys Commun, 1990,59(2):399-415.

[13] John P Perdew, Kieron Burke, Matthias Ernzerhof.Generalized gradient approximation made simple[J].Phys Rev Lett,1996,77(18):3865-3868.

[14] Carlos Sosa,Jan Andzelm,Brad C Elkin,et al.A local density functional study of the structure and vibrational frequencies of molecular transition-metal compounds[J].J Phys Chem,1992,96(16): 6630-6636.

[15] Ducasse L,Fritsch A.Theoretical design of a highspin organic molecule[J].Chemical Physics Letters, 1998,286(3):183-189.

Study on first-principles of electronic structure of Ni[N(CN)2]2

ZU Feng-xia,LIU Min-min
(School of Science,Wuhan Institute of Technology,Wuhan 430074,China)

This paper is devoted to examining the electronic structure and magnetic behavior of molecule-based magnet Ni[N(CN)2]2,using first principles within the full potential linearized augmented plane wave(FP-LAPW)method based on the density functional theory(DFT).The total energy and the density of states and atomic spin magnetic moments are calculated and discussed.Ni[N (CN)2]2is found to stabilize in a ferromagnetic semiconductor.the ferromagnetic interaction originates mainly from the Ni atoms.

density of states;electronic structure;ferromagnetic coupling

O482.54

A

10.3969/j.issn.1674-2869.2010.11.028

1674-2869(2010)11-0104-04

2010-05-27

俎凤霞(1979-),女,山西岚县人,讲师,硕士研究生.研究方向:分子磁体的第一性原理计算.

本文编辑:龚晓宁