超高压容器用钢AISI4340的包辛格系数

刘 兵,袁小会,刘 岑,吴元祥,张红卫,刘小宁*

(1.武汉软件工程职业学院机械制造工程系,湖北 武汉 430205;2.武汉工程大学机电工程学院,湖北 武汉 430074)

0 引 言

为提高单层超高压容器疲劳强度,降低其在操作时的应力水平,对单层超高压容器进行自增强处理,获得有用的预应力是有效的方法;由于超高压容器常用材料的压缩和拉伸屈服应力不一致,对自增强预应力的影响很大,文献[1]认为可用包辛格系数考虑这种影响,文献[2]认为,如无试验数据取包辛格系数为0.86.

文中提出按单层超高压自增强容器[3]塑性层预应力实测值确定钢材包辛格系数的方法,基于试验数据,对超高压容器常用钢材AISI4340的包辛格系数3进行探讨.

1 理论分析

假定超高压自增强圆筒塑性层服从用包辛格系数修正的Mises屈服准则,即

(1)

式(1)中,σt、σr分别为塑性层的周向与径向应力,MPa;m为包辛格系数,m=σsy/σs;σsy、σs分别为材料的压缩和拉伸屈服应力,MPa.

单层超高压自增强圆筒塑性层的周向和径向预应力的计算值分别为[1]:

(2)

(3)

式中,ri、r0分别为圆筒的内、外半径,mm;r为塑性层任一点半径,mm;K为径比,K=r0/ri;pa为实际自增强压力,MPa.

当测得超高压自增强圆筒的塑性层周向预应力σt1或径向预应力σr1时,由式(2)、(3)可得包辛格系数的计算式

(4)

(5)

自增强圆筒的疲劳强度是由剪应力强度决定的,对于单层超高压圆筒,从其在操作时有最小剪应力强度的角度出发,不难得到其在最佳自增强时的弹塑性交界面半径[1,4-5]:

(6)

式(6)中,ropt为在最佳自增强时的弹塑性半径的计算值,mm;pi为操作内压,MPa;E,Et分别为AISI4340钢在常温与操作温度下的弹性模量,MPa;σst为AISI4340钢在操作温度下的拉伸屈服应力,MPa,σst=σsEt/E;pt为当量热压力,MPa,pt按式(7)计算:

(7)

式(7)中,ti、to分别为在操作时圆筒的内、外壁温度,℃;αt为操作温度时圆筒材料的线膨胀系数,1/℃;μ为圆筒材料的泊桑系数,μ=0.30.

2 AISI4340钢的包辛格系数

文献[6]用AISI4340钢制超高压圆筒进行自增强试验,探索恢复超高压聚乙烯反应器自增强预应力的方法;试验条件:AISI4340钢拉伸屈服应力σs=944.4 MPa;圆筒内直径Φ34.7,外直径Φ79.8,径比K=2.30;圆筒塑性层周向和径向预应力的实测值σt1和σr1如表1与表2所示.

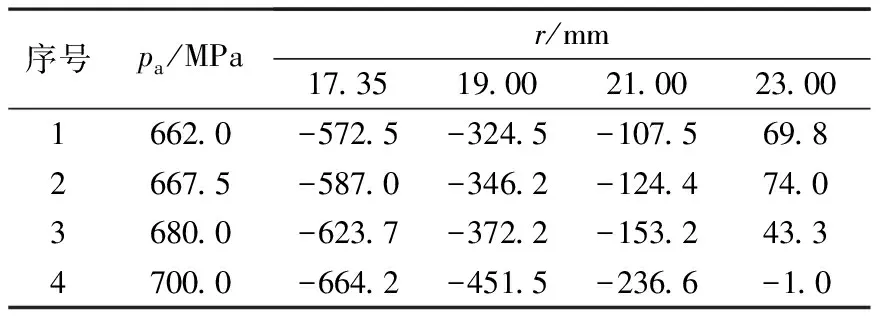
表1 σt1的实测值

表2 σr1的实测值

把表1中的有关数据代入式(4)中可得按塑性层周向预应力实测值确定的包辛格系数,如表3所示.

把表2中的有关数据代入式(5)中可得按塑性层径向预应力实测值确定的包辛格系数,如表4所示.

表3 按σt1确定AISI4340的包辛格系数

注：m1是在同一试验条件下，不同塑料性层位置计算所得包辛格系数平均值;m2是在不同试验条件下，同一塑性层位置计算所得包辛系数平均值.

由表3和表4可知:(1)包辛格系数基本上不受自增强压力大小的影响;(2)包辛格系数的大小与塑性层的位置无关;(3)用σt1与σr1确定包辛格系数无显著差异;(4)由表3、表4得AISI4340钢包辛格系数的平均值为0.967 1.

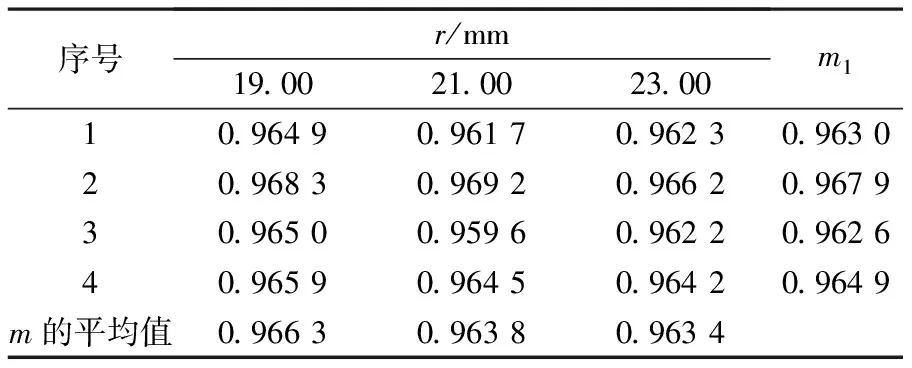
表4 按σr1确定AISI4340的包辛格系数

注：m1是在同一试验条件下，不同塑性层位置计算所得包辛格系数平均值;m2是在不同试验条件下，同一塑性层位置计算所得包辛格系数平均值.

3 工程实例验证

超高压聚乙烯反应器是典型的单层超高压容器,也是生产低密度聚乙烯的关键设备,由于其操作条件苛刻,常常对其进行自增强处理.

我国某石化企业从国外引进的超高压聚乙烯反应器条件如下[4]:第一反应器规格为Φ62×27×8 000(外直径×内直径×长度,mm),原设计者采用自增强弹-塑性交界面半径18.05 mm;第二反应器规格为Φ78×34×8 000,原设计者采用自增强弹塑性交界面半径22.72 mm.

当量热压力由式(7)计算:

当采用文中包辛格系数0.967 1及式(6)计算最佳自增强时的弹-塑性交界面半径时,由于pi-pt=261.0 MPa,对于第一反应器有

=18.12 mm

相对误差:(18.12-18.05)/18.05×100%=0.41%.

对于第二反应器有

=22.81 mm

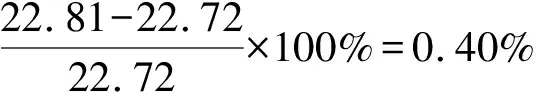
因此,用上述方法计算AISI4340钢制超高压容器最佳自增强时的弹-塑性交界面半径是合理的.

4 结 语

超高压容器用钢AISI4340的包辛格系数是一个常数,其大小与塑性层的位置和容器自增强压力的大小无关.AISI4340钢包辛格系数的平均值为0.967 1.工程实例验证表明,用文中方法计算AISI4340钢制超高压容器最佳自增强时的弹-塑性交界面半径是合理的.

参考文献：

[1]邵国华,魏龙灿.超高压容器[M]. 北京:化学工业出版社,2002.

[2][日]HPIS-C-103-1980.超高压圆筒容器设计指针[S].

[3]蔡洪涛.压力容器法兰的参数化绘制方法[J].武汉工程大学学报，2010，32(9)：86-89.

[4]华南工学院高压容器研究室. 自增强容器最佳超应变的实验研究[J].压力容器,1984,1(2):17-24.

[5]刘小宁.超高压管式反应器的最佳弹性-塑性交界面半径[J].化工设计,2006,16(5):29-30,42.

[6]陈进锋,陈国理.恢复超高压聚乙烯反应管自增强残余应力[J].石油化工设备,1987,16(9):23-27.