关于CFD验证确认中的不确定度和真值估算
张涵信,查 俊
(中国空气动力研究与发展中心,四川绵阳,621000;国家计算流体力学实验室,北京,100191)
0 引 言
随着计算机技术、计算格式及网格技术等的发展,计算流体力学(CFD)取得了长足的进步,在基础研究及工程的应用方面日趋广泛。然而CFD方法的的可信度(不确定度)或可靠性一直是关心的问题。
AIAA在1998年发布的《Guide for the Verification and Validation of CFD Simulations》中对误差(error)和不确定度(uncertainty)给出了如下见解:
误差是建模和模拟过程中可认知的缺陷,不是由于知识缺乏导致的。(A recognizable deficiency in any phase or activity of modeling and simulation that is not due to lack of knowledge.)而不确定度是由于知识的缺乏,在建模和模拟过程中潜在的缺陷。(A potential deficiency in any phase or activity of the modeling process that is due to lack of knowledge.)
而Roache[1]把误差定义为计算值或试验值与真实值的差别。当真实值不确定或者不可知时,计算值或试验值的误差就不能确定,这时不确定度就是误差的估计。
尽管国外的工作已有很多关于这方面的研究[1-15],但是对于CFD不确定度方面的一些基本概念还是缺乏明确和好用的定义。
CFD计算结果误差的来源一般分为四类[2]:物理模型误差、离散误差、计算机舍入误差、程序设计误差。
(1)物理模型误差:其主要源于不精确的物理模型,也就是说,控制方程和边界条件不能充分地描述要模型化的物理现象。例如湍流模型、流动由层流到湍流的转捩模式的误差、气体状态方程与真实情况之间的误差以及边界条件表述的误差等。
(2)离散误差:其主要来源与各种数值方法对控制方程及边界条件的离散化,因空间离散和时间离散的有限精度以及有限分辨率导致数值解与所求解方程的精确解之间存在误差;空间网格及表面网格不够密和不够光滑所带来的误差[3,16]。
(3)舍入误差:源于计算机数据存储字长的限制。
(4)程序设计误差:这是简单的失误,可以归为上述未提及的误差。并且一般可在使用某些方法或者在程序验证过程中发现这些错误。
此外,还有迭代如何判定收敛的误差。
CFD计算模拟的不确定度可以分为以下两类[17]:
(1)模型形式不确定度:它是指数学模型描述实际物理系统的真实行为时的不确定度,也称为结构不确定度或者非参量化不确定度。这种类型的不确定度很难用概率密度函数来描述。在CFD中,湍流模拟即属此类。
(2)参量不确定度:它是CFD中某些参量(包括网格、算法中的系数)其精确的结果无法得到而产生。
在文献中,不确定度分析方法有以下几种[17]:I.非概率方法(Non-probabilistic Methods)
这里又可分为:
(1)区间分析(Interval Analysis)方法:给出计算值的上限和下限,从而确定不确定度。但要求可能的计算值不能遗漏。
(2)误差传播的敏感性导数(Sensitivity Derivatives)方法:其基本思想是量化输出结果对输入参数微小变化的灵敏度,从而分辨出各种输入量对于输出结果不确定度的影响。
(3)模糊逻辑(Fuzzy Logic)方法:模糊逻辑方法是对不精确、不完善的计算结果中输入参量的不确定范围,利用模糊逻辑和模糊规则进行推理分析,从而确定结果的不确定性。在CFD领域现还很难使用。II.概率方法(Probabilistic Methods)
(1)常用的是Monte-Carlo方法[4,18]。该法首先假设概率密度函数计算输入参量的误差,形成样本,然后求计算样本值的确定性结果,再对确定输出结果进行统计分布(如均值、方差)给出不确定度。
Monte-Carlo方法的计算成本相当高昂,因此发展了许多修正方法。但由于输入量的概率密度函数的确定是否合宜,Monte-Carlo方法的结果仍有问题。
(2)矩量法(Moment Method)[5,19,20]
该法给定可用的一阶(均值)、二阶(方差)、三阶(偏度)和四阶矩(峰度)来表示概率分析的特征,然后来确定概率分布,从而确定不确定度。
III.随机微分方程方法(Stochastic Differential Equantion Method)[6]
它是在CFD确定性方程中加入输入量的随机变量来计算CFD模拟过程的不确定度。随机微分方程方法已应用于结构力学问题中,但最近才开始应用于CFD不确定度研究中。
以上情况表明,误差的定义、来源是明确的。由于真值不能确定,不确定度就定义为对误差的估计,但什么叫误差的估计也是不明确的。关于不确定度的理论、方法,虽已提出不少,但能够具体应用的不多。这就给飞行器CFD的实验和确认造成了困难。
飞行器的CFD验证、确认,一般是这样进行的:选定飞行器外形(根据需要确定一个或多个),指定来流条件和要验证的量,分别委托各实验部门和CFD部门,各进行实验和计算。一般各实验部门的实验数据各不相同,各计算部门提供的计算数据也不一致。实验部门必须给出实验结果的真值和不确定度(或可信度)。计算部门也必须给出计算结果的真值和不确定度,然后两者进行比较,完成验证与确认。但实际上,由于真值和不确定度现在还没有理论确定,因此,验证、确认的结果,只是给软件提供者给出他的结果与实验及其他计算结果的对比情况。对其计算软件和真值差多远,得不到确定的结论。这是现有验证、确认存在的不足。
本文的目的是在不确定度、误差等术语[21]和试验中使用的定义[22,23]相同的情况下,给不确定度一个新的解释方法,从而可给不确定度一个新的表达式,以此为基础,可给出真值的估计方法以及真值的近似表达式。这样就容易在CFD验证和确认中作出应用和判断。
1 CFD不确定度和真值的估算方法
1.1 CFD不确定度表达式
同实验所用的概念一样,我们把数值解 xC与真值C之差的绝对值的最大值,即:

称为不确定度。把
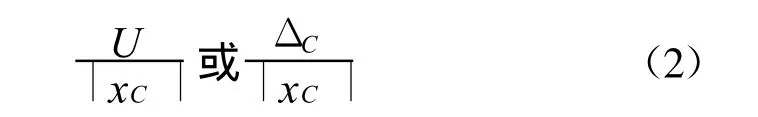
称为相对不确定度。
CFD的不确定度我们可以提出另一种说法来表达。大家知道,工程制造上是按设计数据加工的,常有一种说法,加工能达到形状,可准确到设计数据前几位,这也是表示准确度的一种说法,我们不妨也采用这种方法来表述计算的准确度。即采用计算值可达到真值的前n位来表示计算结果的不确定度。设气动系数C可表达为:
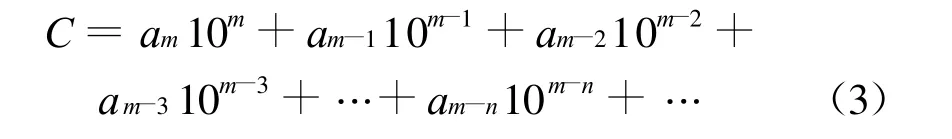
如果要求前n位真值准确,它可写成:

显然Δ应满足** ΔC也可表述为×10m-n+1,此时所作的结论小1倍。:

式中,1drag count=10-4。
即绝对不确定度为:

相对不确定度为:

或近似可写成
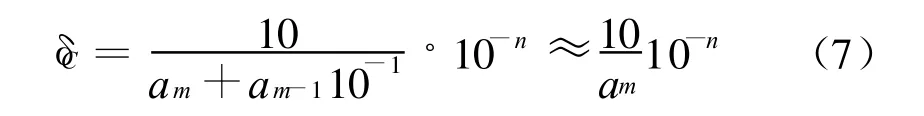
可见,如果n=2,即前两位真值准确,相对不确定度为[10/(am+am-1 10-1)]%;如果n=3,相对不确定度为[10/(am+am-1 10-1)]‰;如果n=4,为万分之10/(am+am-110-1)。这种表示方法对实验测量值和计算值均可运用。
对运输机,如取n=3,即前三位真值准确,CL,Cm,CD的不确定度是:

若给出 δCL,δCm,δCD,它们分别是 :
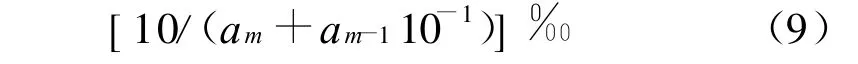
这里am表示CL,Cm及CD的第1位出现的值。大家知道,式(8)-(9)正是现在实验能达到的绝对和相对不确定度。
1.2 真值的估算方法
设Ct为计算值,C为真值,则Ct-ΔC≤C≤Ct+ΔC。这表明,计算结果满足前n位真值准确的数据带的带宽应该为:
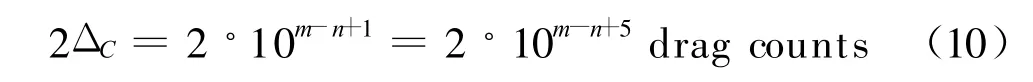
如果一个量有多种计算方法给出计算结果,将它们的数据画出,就可给出一个数据带。若这个数据带满足式(10),这里面的数据就满足前n位真值准确。这样我们就确定了真值的前n位。
做为例子,对运输机,表1给出了运输机的数值带宽2ΔCL,2ΔCm及2ΔCD与n的关系。当数据带落在n的范围内时,真值前n位就可确定。
用这种方法,我们可以进一步估算真值。事实上要更准确的估算真值(计算值或者实验值),需作大量的计算或实验。即需要大的数据样本,此时可引用大数定律和统计理论。

表1 n与2ΔC的关系Table 1 Relations between n and 2ΔC
设多个计算或多个实验值给出的离散数据ξ为xi,i=1,2,…,且 P(ξ=xi)=Pi为其出现的概率,则加权平均值x

是ξ的数学期望,对任意的ε>0,其出现的概率满足:
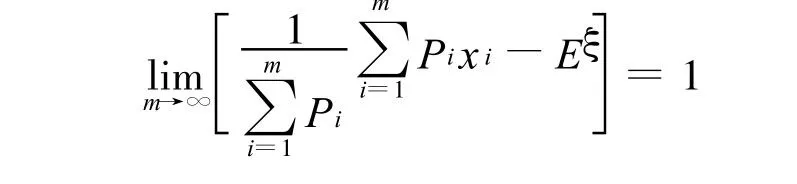
若称Δi=|xi-x|为方差,其
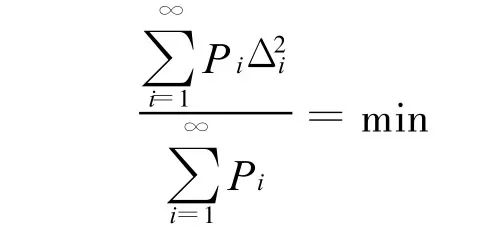
这表明,当数据样本m足够大时,加权平均值
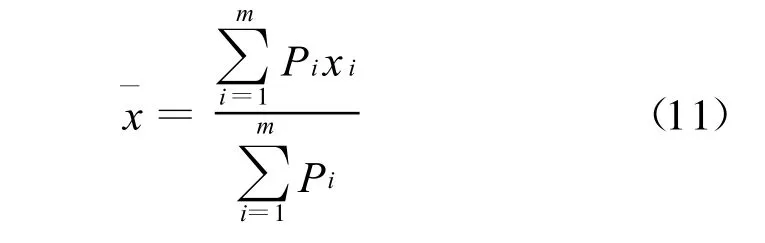
是样本中最可能出现的。当已知数值满足前n位真值准确后,以此可给出真值的估算方法,建议分两步进行:
(1)预测:
先预计一个权分布。例如在CFD的求解中,网格数越大,模型越好,计算方法精度越高,边界处理越好,一般求解越准确,Ni就越大。可以把 Ni先作为权,于是加权平均值可表达为:

这里xi为计算值或实验值。
令|xi-|=Δi,因 Δi越大,偏差越大。因此可用qi=作为进一步的权值,此时可得:

式(13)即可作为预测的真值,从而确定数据(x1,x2…xm)接近真值几位,可以证明,它的误差是:

(2)修正
在决定各计算值或实验值接近真值的预测的位数后,例如n=2,在这种情况下,我们把预测中已经准确到2位的数据集中起来,略去不到2位真值准确的数据。然后利用预测步的第二步公式进行重新计算,这样得到的结果可能是2位真值准确的最优结果。我们称之为最优解或最优值。用这个解,再回头评价各个CFD软件或实验结果,从而分别给出对它们精度的评价。
2 应用举例
2.1 模型方程确定,用CFD求解NS方程给出驻点压力、热流和摩阻的验证
为简单,这里仅讨论高超声速圆柱绕流。来流条件为:M∞=8.03,T∞=124.94K,Tw=294.44K,Re=1.835×105,壁面采用等温壁条件。这个例子有实验结果[24]。
求解分别用了三种方法:NND格式、三阶紧致(CC3)、五阶紧致(CC5),每个方法中分别用4套网格,由于每套网格中壁面附近最小网格Δhmin又有两种不同,所以可以说每种算法中有八套网格。表2~表4分别给出计算得到的驻点压力、摩阻系数及驻点点热流的结果。
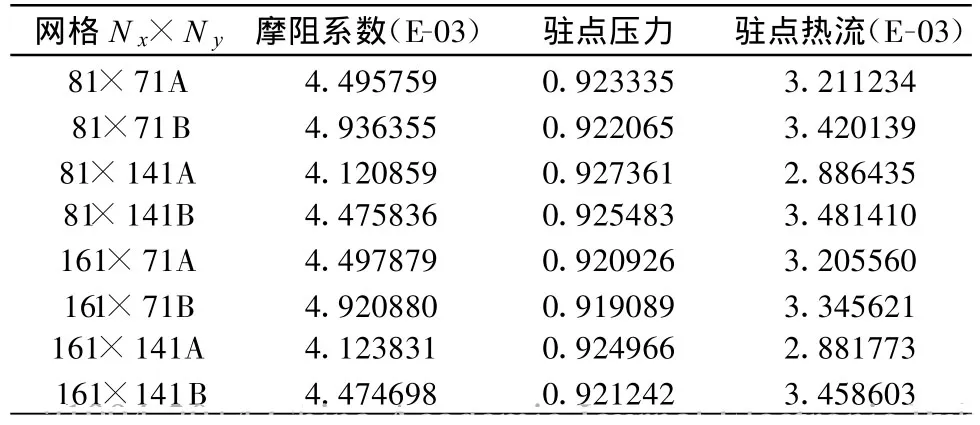
表2 NND的结果Table 2 Computed results using NND schemes
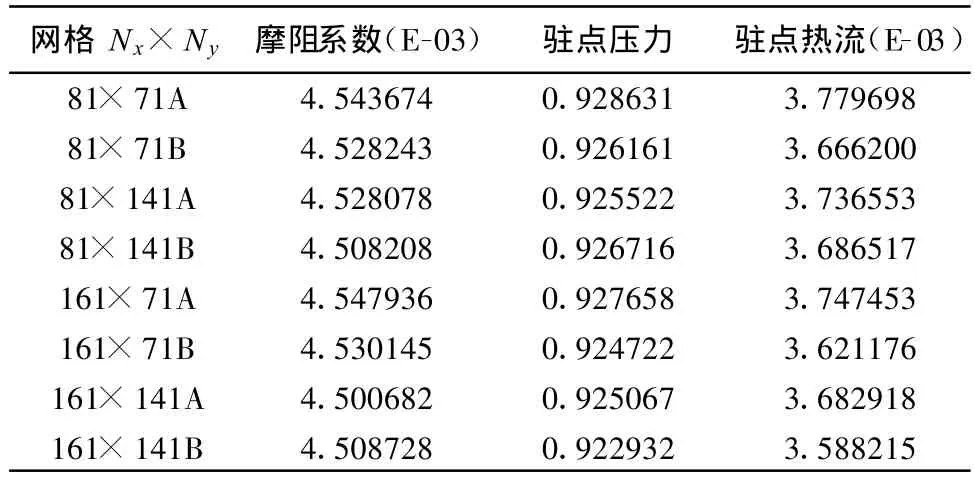
表 3 CC3的结果Table 3 Computed results using CC3 method

表 4 CC5的结果Table 4 Computed results using CC5 method
表5是利用上节理论给出的最优解及其相应的误差,还列出了实验结果。可见,计算给出的真值,与经认真检验的实验值相当接近。这说明,本文的真值估算方法是正确有效的。
表6是根据最优解给出各个计算结果的比较。
2.2 DPW第二次验证会议阻力数据的分析验证
这里仅引用DLR-F6无发动机舱的各家阻力计算数据[25,26]。
表7是网格数与相应阻力系数的数据表(它是根据图读出来的),计算条件是:M∞=0.75,Re=3×106,CL=0.5。
表8给出了根据上节理论给出的最优值,它与实验值相当接近。这再次说明,本文真值估算方法是满意的。
图1还画出了两位真值准确数据带。
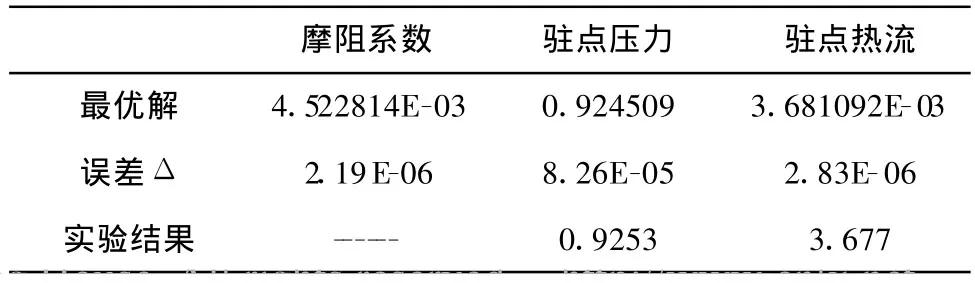
表5 最优解的结果Table 5 Optimum computed results
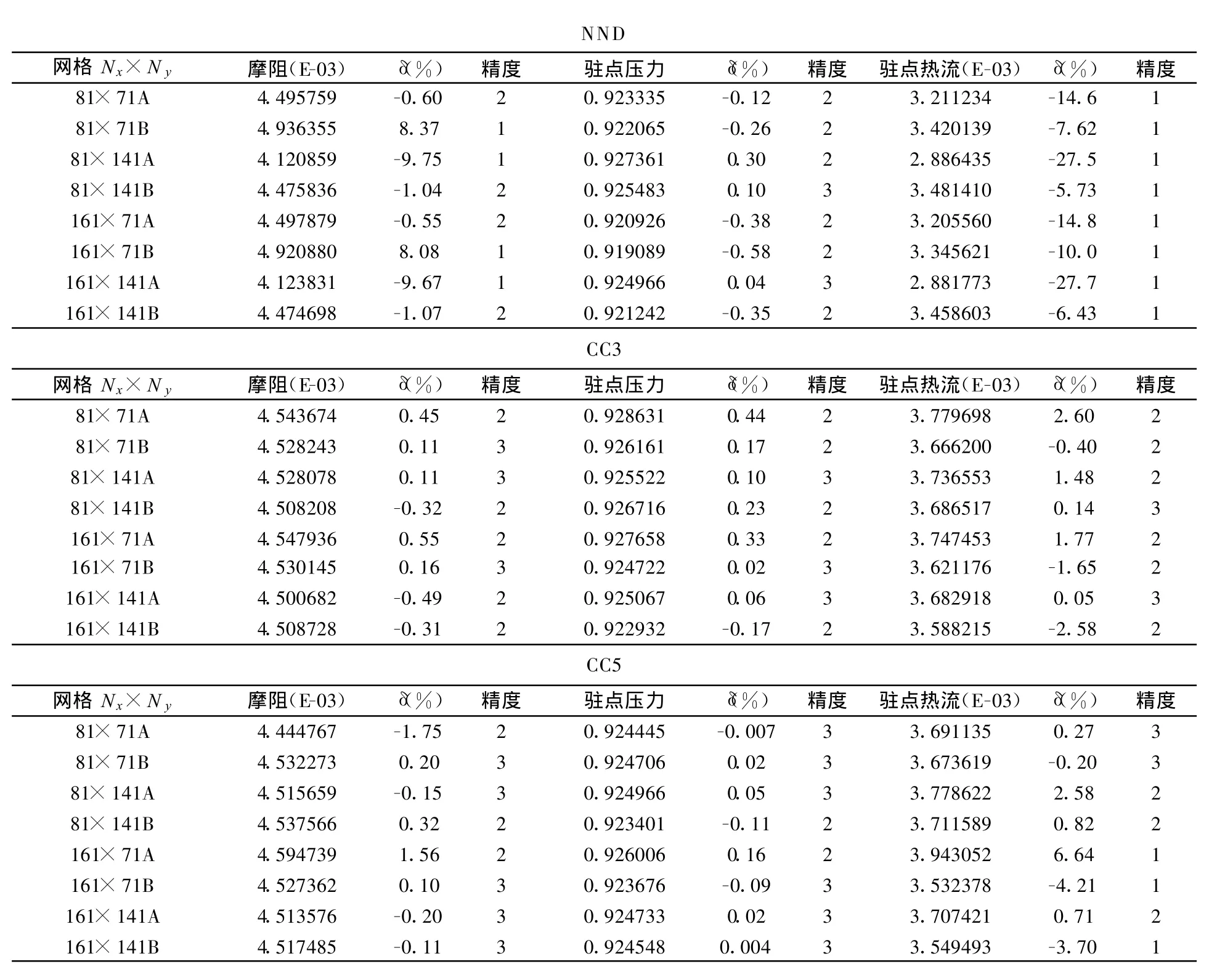
表6 各软件结果的比较Table6 Comparison of computational results given by different codes
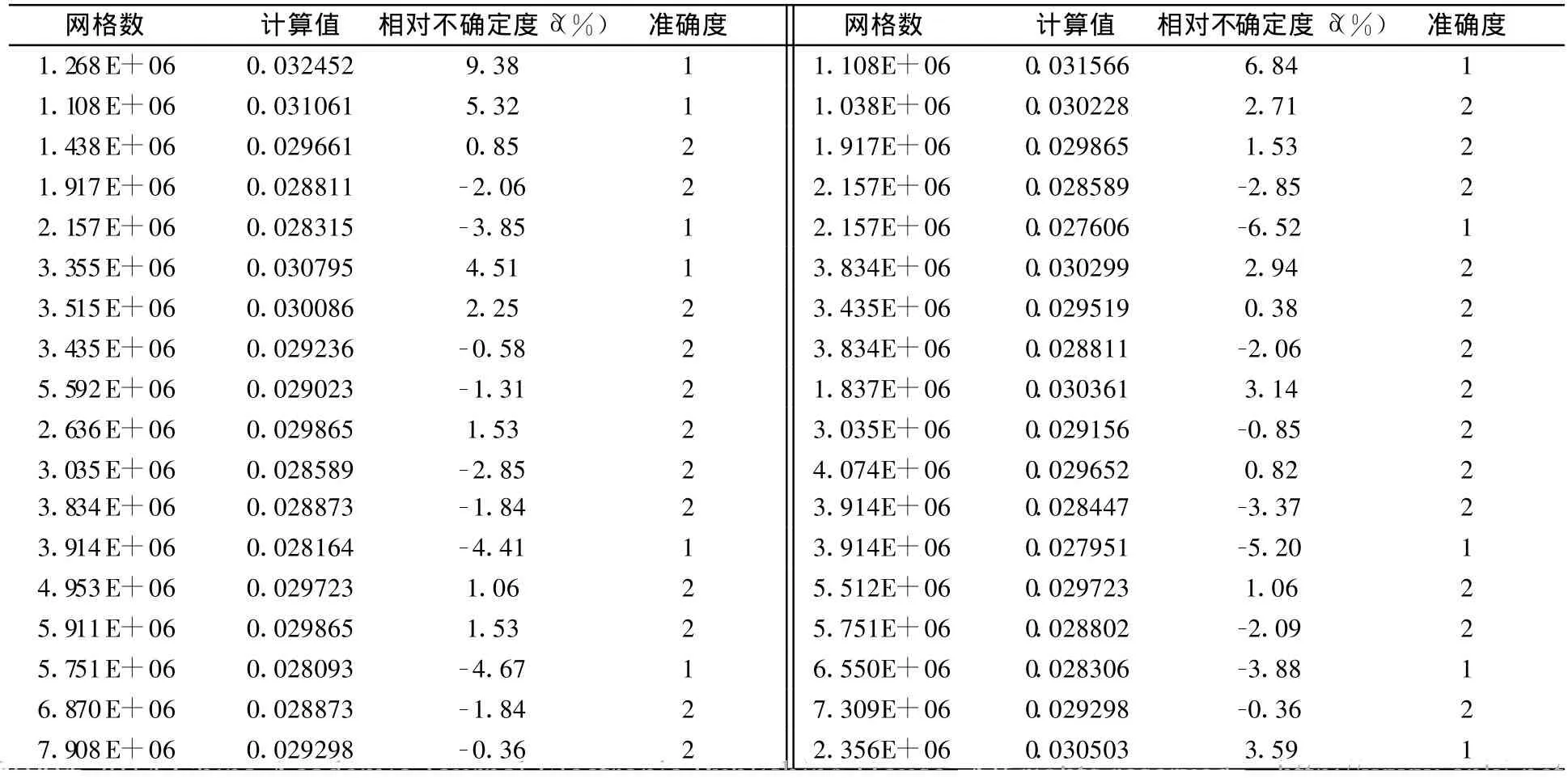
表7 网格与阻力系数的数据表Table7 Drag coeff icients and grids

5.252E+06 0.029298 -0.36 2 6.270E+06 0.029865 1.53 2 4.114E+06 0.027384 -7.38 1 2.836E+06 0.025825 -13.8 1 6.271E+06 0.029865 1.53 2 6.510E+06 0.029014 -1.35 2 8.188E+06 0.029440 0.11 3 8.667E+06 0.028660 -2.60 2 8.827E+06 0.028589 -2.85 2 9.086E+06 0.028235 -4.14 1 1.010E+07 0.029794 1.30 2 9.945E+06 0.029298 -0.36 2 9.546E+06 0.029156 -0.85 2 9.945E+06 0.028660 -2.60 2 1.130E+07 0.027810 -5.73 1 1.322E+07 0.028306 -3.88 1 1.258E+07 0.029227 -0.61 2 2.312E+07 0.029014 -1.35 2 2.256E+07 0.028306 -3.88 1 2.256E+07 0.027951 -5.20 1

表8 最优解的结果Table 8 Optimum computed results

图1 二位真值准确的数据带Fig.1 Thezoneof approximating to first twodigil number of truth value
3 结 论
本文回顾了CFD验证、确认中不确定度的概念和研究方法,CFD的不确定度尚无表达式可以使用。本文也讨论了现在正在进行的实验验证,对各个参加验证的软件,如何作出定量的精度评价也缺乏原则。针对这些情况,我们在不改变不确定度定义的前提下,对不确定度作了新的解读,即不确定度可解读为计算值或实验值与真值准确到前n位,从而可给出不确定度的表达式和真值估算的原则。并根据大样本数据的统计理论,对真值认为接近数学期望,从而给出准确到n位真值的计算方法。这个方法,可用于计算结果的检验,例如当模型一定时,可用此法寻求计算方法的真值,对算法进行检验;如算法一定模型改变时,也可用于检验模型的可靠性。利用这种方法,在没有实验结果的情况下,也可评价各计算软件的质量。文中方法当然也可以运用处理实验数据。因为CFD中计算模型是人为建立的,虽然可以检验它的解是否正确,但与物理情况是否一致,并未得到回答。因此,开展实验验证及确认是必需的。
[1]ROACHE P J.Verification of codes and calculations[J].AIAA Journal,1998,36(5):696-702.
[2]OBERKAMPF W L,BLOTTNER F G.Issues in computational fluid dynamics code verification and validation[J].AIAA Journal,1998,36:687-695.
[3]ROACHE P J.Quantification of uncertainty in computational fluid dynamics[J].Annual Review of Fluid Mechanics,1997,29:123-160.
[4]WALTERSR W,HUYSE L.Uncertainty analysis for fluid mechanics with applications[R].NASA/CR-2002-211449,ICASE Report No.2002-1,2002.
[5]PUTKO M M,NEWMAN P A,TAYLOR A C,GREEN L L.Approach for uncertainty propagation and robust design in CFD using sensitivity derivatives[R].AIAA Paper,2001:2001-2558.
[6]MATHELIN L,HUSSAINI M Y,et al.Uncertainty propagation for turbulent,compressiblef low in a quasi-1D nozzle using stochastic methods[A].16thAIAA Computational Fluid Dynamics Conference[C].Orlando,Florida,AIAA,2003:2003-4240.
[7]LUCOR D,XIU D,et al.Predictability and uncertainty in CFD[J].Int.J.Numer.Meth.Fluids,2003,43(5):483-505.
[8]OBERKAM PF W L,TRUCANO T G.Verification and validation in computational fluid dynamics[J].Prog.Aero.Sci.,2002,38:209-272.
[9]LUCKRING J M,HEMSCH M J,MORRISON J H.Uncertainty in computational aerodynamics[R].AIAA-2003-0409,2003.
[10]RAYMOND R,et al.Theimportanceof uncertainty estimation in computational f luid dynamics[R].AIAA-2003-0406,2003.
[11]FREITAS C J,GHIA U,CELIK I,ROACHE P,RAAD P.AMSE'S quest to quantify numerical uncertainty[R].AIAA-2003-627,2003.
[12]ROACHE J.Need for control of numerical accuracy[J].J.Spacecraf t and Rockets,1990,27(2):98-102.
[13]COLEMAN H W,STERN F.Uncertainties and CFD code validation[J].Journal of Fluids Engineering,1997,119(4):795-803.
[14]Quantifying uncertainty in CFD[J].Journal of Fluids Engineering,2002,124(1):2-3.
[15]B.DE VOLDER,GLIMM J,GROVE JW,KANG Y,LEEY,PAO K,SHARP D H,YE K.Uncertainty quantification for multiscalesimulations[J].Journal of Fluids Engineering,2002,124(1):29-40.
[16]ROACHE P J.Quantification of uncertainty in computational fluid dynamics[J].Annual Review of Fluid Mechanics,1997,29:123-160.
[17]FA RAGHER.Probabilistic methods for the quantification of uncertainty and error in computational fluid dynamics simulations[R].DSTO-TR-1633,2004.
[18]HAMMERSLEY J M,HANDSCOMB D C.Monte Carlo methods,methuen's monographs on applied probability and statistics[M].Flether&Son Ltd.,Norwich,1964.
[19]HUYSE L.Free-form airfoil shape optimization under uncertainty using maximum expected value and secondorder second-moment strategies[R].Tech.Report,ICASE Report 2001-18/NASA CR 2001-211020,2001.
[20]HUYSE L,LEWIS RM.Aerodynamic shapeoptimization of two-dimensional airfoils under certain conditions[R].Tech.Report,ICASE Report 2001-1/NASA CR 2001-210648,2001.
[21]张涵信.关于CFD计算结果的不确定度问题[J].空气动力学学报,2008,26(1):47-49.
[22]恽起麟.风洞实验[M].近代空气动力学丛书,国防工业出版社,北京,2000.
[23]程厚梅等.风洞实验干扰与修正[M].近代空气动力学丛书,国防工业出版社,北京,2003.
[24]WIETING A R.Experimental study of shock wave interference heating on a cylindrical leading edge[R].NASA TM-100484,1987.
[25]LAFLIN R,et al.Summary of data from the second AIAA CFD drag prediction workshop(Invited)[R].AIAA-2004-0555,2004.
[26]HEMSCH M J,M ORRISON J H.Statistical analysis of CFD solutions from 2nd drag prediction workshop[R].AIAA 2004-556,2004.

