网格之间流场信息传递的高精度方法和验证

刘 君,白晓征,王 巍

(1.国防科技大学航天与材料工程学院,湖南长沙 410073；2.空军装备研究院装备总体论证研究所,北京 100076)

0 引 言

网格分区技术是结构网格求解复杂外形的基础,广泛应用的主要有重叠(overlapping)网格技术和对接(patched)网格技术两类,计算过程中,首先采用流体力学解算器分别求解各子区域网格上物理量,然后通过边界上信息传递,从而完成整个流场的计算。实际问题中相邻子区域的边界网格或重叠部分网格很少在位置上正好一一对应,因此需要采用一定的算法传递相邻子区域的信息。对于包含有激波等间断的流场模拟,目前常用线性插值或其他高精度插值方法,插值表达式通常为多项式,用网格自身及其周围单元的信息来确定多项式的系数；线性插值优点是满足单调性、守恒性、形式简单、效率高,但是只有一阶精度,数值耗散大；高精度插值提高精度,但是涉及到网格内物理量导数计算,而且在应用非结构动网格技术和插值方法求解分离问题时发现,网格重构以后流场出现的非物理振荡会导致气动力明显的波动[1,2]。

在文献[1]中给出一种新的信息传递算法,充分利用时间推进的特点,采用移动网格的方法,随着时间推进完成旧网格信息到新网格的传递。这种新的流场信息传递算法与插值方法的原理完全不同,理论可以证明信息传递过程没有引入误差。文献[1]中针对一维和二维问题,比较了新的信息传递算法和插值方法,给出了传递过程中时间推进步长的稳定性条件。

本文进一步分析了插值方法引入误差的原因,然后在介绍新的信息传递算法原理基础上,推导了三维情况下传递过程时间推进步长的稳定性条件,最后给出了三维算例。

1 插值方法引入误差的原因分析

由于系数γl与网格空间分布间距Δx相关,计算得到的流场参数与网格分布相关,在其他条件相同的情况下,不同网格分布在同一物理位置的数值解也不相同。

设有两套网格,在同一物理位置x P处,根据差分方程得到第二套网格数值解为uP,根据第一套网格结点变量插值得到的该点值为u T。插值方法是相同时刻不同空间位置物理量之间的关联,可以写为二者之间距离的函数:

数值解uP满足修正方程,将上式带入修正方程(1)中,略去高阶小量,得到:

理论上uP和u T时间空间相等,如果假设uP和u T随时间变化导数相等,根据上式可以推导出插值过程不影响差分方程数值解的条件:

由于插值方法和有限差分法相互独立,不可能严格满足以上条件,因此得出结论:插值过程必然引入误差,导致流场计算过程精度降低。

根据CFD理论,对数值解影响较大的是修正方程第一项,假设第一项中没有插值误差就认为对有限差分法不影响。如果差分格式具有一阶精度,为了保证修正方程第一项中系数γ2～o(Δx)不受影响,要求式(4)为高阶小量,即r≥4；如果差分格式具有二阶精度,保证第一项中系数 γ3～o(Δx2),要求 r≥6,线性插值和ENO插值都达不到这样的要求,因此插值以后出现明显波动[1]是不可避免的。

2 动网格传递流场信息的基本原理

在两套网格间进行流场插值或信息传递前,首先需要确定网格间的关系。以重构后新旧网格为例,需要确定新网格的网格单元中心位于旧网格区域的哪个单元内。在插值方法中,首先假设物理量的分布形式,如线性分布、抛物型分布,然后通过贡献单元及其周围单元的信息构造出分布系数,最后得到新网格中心点的物理量,或者通过守恒型算法计算新网格单元内物理量的平均值。

与插值方法不同,信息传递算法并不显式地指定物理量的分布形式。它的基本原理是,采用动网格技术,让旧网格中心点在有限的时间内运动至新网格中心处,在移动网格的同时求解ALE形式的流动方程,从而得到新网格中心点的物理量。下面以二维为例介绍这种信息传递的原理。图1(a)中,O点为n时刻旧网格的中心,n时刻物理量已知；P和Q是新网格中两个单元的中心点。为了得到新网格P点的物理量,采用移动网格技术,保持O点附近网格不变形,在Δt时间内将旧网格单元从O点平移至P点,如图1(b)所示,移动网格的同时求解流场,得到N+1时刻O′处物理量值,也即新网格单元中P点的值；同样,在旧网格基础上,还是从n时刻流场参数出发,保证时间方向同样推进Δt,同时平移网格使得O点在n+1时刻移到Q点,得到Q点n+1时刻的物理量。对新网格中每一单元重复此过程,即可得到新网格在n+1时刻的流场,在此基础上放弃旧网格、采用新网格继续计算,如图1(c)所示。

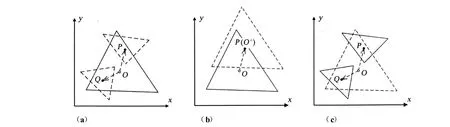
图1 信息传递原理演示Fig.1 Sketch map of the new method

从原理上可以看出,以上信息传递方法是一种全新的思想,与插值方法有明显不同:

(1)插值方法在同一时间层内利用空间关联完成信息传递,即用n时刻O点及其相邻点参数得到n时刻P和Q点处流场参数,然后采用新网格继续计算；本文信息传递方法利用时间推进在两个时间层内完成。

(2)上一节已经证明插值必然引入新的误差,本文方法通过求解流动方程完成流场信息传递,得出的时刻流场参数与原有限体积方程完全相容,信息传递过程本身不会带来额外误差。

(3)插值方法与流动控制方程无关,其精度与假设的物理量的分布形式有关；本文方法通过求解流动方程实现信息传递,并不显式假设物理量的分布形式,其精度即为流动求解器的精度。

采用本文方法进行信息传递时,为了保证n+1时刻的流场同步性,整个需要传递信息的区域应当使用根据稳定性条件确定的统一的最小时间步长Δtmin。当新旧网格之间移动距离较大时,网格移动在一个Δt时间内无法实现,需要采用多步进行。从CFD计算方法构造过程知道,采用时间显式格式推进时,从n时刻推进到n+1时刻仅需要相邻网格的n时刻流场,推进到n+2时刻则要相邻网格n+1时刻流场,本质上涉及到相邻网格以外更远区域的n时刻流场。采用多步推进时,把移动区域扩大了,会使得计算过程更为复杂,计算量增大。因此,需要确定满足Δtmin要求的最少时间推进步数,这就涉及到移动网格过程中的稳定性条件。

在文献[1]中给出了一维和二维问题的稳定性条件,下面推导三维问题的稳定性条件。

3 三维稳定性条件

如图2示意的四面体,新网格中心点P位于中心点O的旧网格四面体ABCD中,假设O点在时间Δt内移动到P点,根据下式计算网格移动速度:

假设采用时间显式格式的有限体积方法,稳定性条件为:

进一步化为更严格的限制条件:

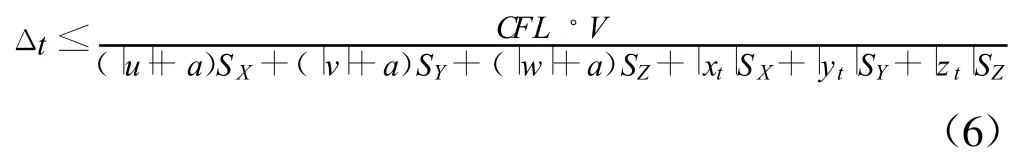
其中SX、SY和SZ为四面体ABCD在三个坐标平面的投影面积。联立方程式(5)、(6),得到:

定义三维动网格Courant数NV为:

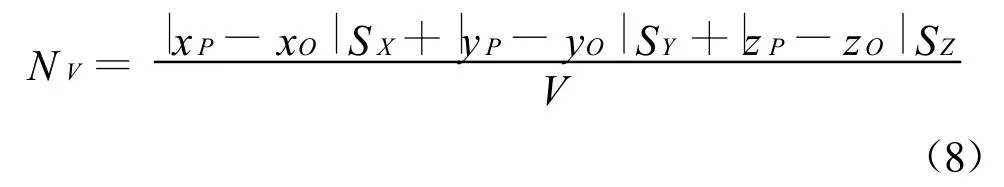
可以看出,NV与各点坐标绝对值大小及流动变量无关,仅取决于新旧网格的相对位置和旧网格的形状参数。为便于分析,采用坐标系平移使O点位于原点,O点与旧网格的4个顶点相连,形成4个四面体,包含新网格P点的四面体记为ABCO,坐标系旋转使得P点位于z轴负向,如图2所示,设OP延长线与ΔABC平面交点为H。在 xoy平面内,ΔABC和D点的投影分别记为Δabc和d,由于P点位于四面体ABCO中,O点必然落在Δabc内,利用这一特性分析特征投影面积SZ的取值范围。

图2 NV取值范围的证明过程Fig.2 Proving process of the varying range of NV

如果d点落在Δabc内部,那么 SZ=Sabc。如果d点不在Δabc内,分为d点在线段ab外侧和d点在c点外侧两种情况,如图2中示意,ab中点记为e,cd中点记为f。O点为四面体重心,有:xa+xb+xc+xd=0和y a+yb+y c+y d=0,推出 e点和 f点满足的关系:

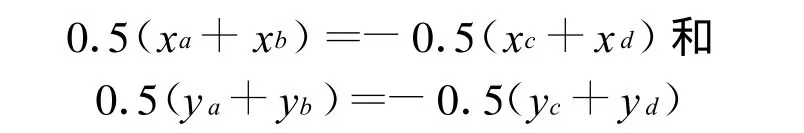
(1)对于d点在线段ab外侧情况,两个四边形面积相等Safbc=Safbd=SZ,由于Sabc≥Safbc,得到:Sabc≥Z。

由于 NV≤3,对稳定CFL数为1的显式格式,根据式(7),网格移动可以在3步内完成。

按照以下关系可以得到满足全流场稳定性和动网格Courant数的时间推进步长:

即新网格中点P位于任意四面体ABCD中,三步内可以将O点移动到P实现流场信息传递。

4 算例验证

设计如下图3所示意的激波诱导物体运动问题,两圆柱位于长∶宽∶高=2∶0.25∶1的矩形计算区域内,其中质心为(-0.4,0.78,0.125)的圆柱固定不动,质心为(-0.4,0.22,0.125)的圆柱的无量纲质量为m=1,不考虑重力和摩擦力等因素,圆柱运动特性完全由气动力控制,可以自由移动。在环境大气条件下,激波马赫数 M∞=2.96进入计算区域与物体相互作用,产生绕射、反射等非定常流动现象的同时,采用动网格技术开展流动模拟,具体计算方法、几何守恒律等问题参见文献[3]。

图3中给出无量纲时间为t=0.2和t=0.4的压力云图,计算中在t=0.332时网格变形严重,需要进行局部网格重构,重构前后物体附近网格见图4。分别采用线性插值、Weighted Least-Squares[4-5]插值方法和动网格信息传递方法得到重构后网格点的流场参数,然后继续计算。

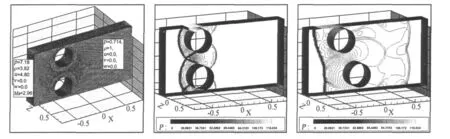
图3 计算区域、网格和不同时刻流场压力云图Fig.3 Computational model,grids and pressure contours

图4 重构前后局部网格Fig.4 Grids beforeand after remeshing

图5给出不同方法得到的圆柱受力情况,不同的信息传值方法有明显差异,动网格信息传递没有引入新的误差,作为比较基础,分析如下:

(1)对于静止圆柱,尽管物体附近网格没有进行重构,由于处于运动圆柱插值区域马赫锥内,还是受到插值误差影响,大致t=0.36开始轴向力FX出现变化,插值误差随流动向下游传播,到t=0.39前FX逐渐趋近于本文方法的计算曲线。法向力FY到了t=0.42以后三条曲线才开始明显区别,说明插值误差影响机理较为复杂。

(2)对于运动圆柱,线性插值以后立刻引起轴向力F X剧烈变化,通过流场动画比对,在t=0.39以后计算曲线的两次波动是插值误差经过壁面和另一圆柱反射所致。法向力FY在t=0.35前两种插值计算曲线和本文方法的比较一致,到了t=0.41后两种插值计算曲线之间相差较大,本文方法计算曲线落在它们之间,变化规律不一致。

通过算例,可以看出插值方法引入误差在流场内扩散规律较为复杂,本文方法计算曲线光滑,验证了前面的分析结论。

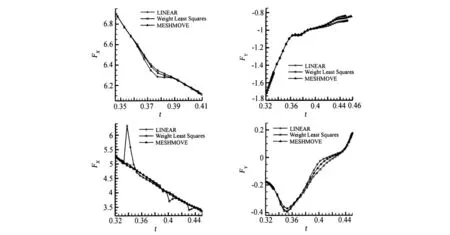
图5 上:静止圆柱受力 下:运动圆柱受力Fig.5 Aerodynamic forces for the steady column(above)and the moving column(below)

5 结束语

理论和实际算例表明,新的信息传递算法比目前常用的插值方法精度高,通过本文工作把这一方法推广到三维有限体积方法中,解决了其应用到复杂流场时遇到的难题。

[1]LIU J,BAI X Z,GUO Z,et al.A new method for transferring flow information among meshes[J].Computational Fluid Dynamics Journal,2007,15(4):509-514.

[2]白晓征,郭正,刘君,等.非结构动网格方法中的若干问题研究[A].中国第一届近代空气动力学与气动热力学会议论文集[C].绵阳,2006:301-306.

[3]刘君,白晓征,郭正,等.有相对运动多体动力学系统流动计算方法若干问题讨论[J].空气动力学学报,2008,26(1):14-18.

[4]ZEEUW D L D.A quadtree-based adaptively-refined Cartesian-grid algorithm for solution of the Euler equations[D].the University of Michigan,1993.

[5]HUNT JD.An adaptive 3d Cartesian approach for the parallel computation of inviscid flow about static and dynamic configurations[D].The University of Michigan,2004.