大跨度空间结构典型形体风压分布风洞试验研究现状

李元齐 ,胡渭雄 ,王 磊

(同济大学建筑工程系,上海200092)

0 引 言

大跨空间结构是近三十多年来发展最快的结构形式[1],其被广泛地应用于体育场馆、会展中心、影剧院、机场航站楼等大型公共建筑中。为了获得更大的无柱空间,克服自重对结构跨度的束缚,人们不断探索采用轻质高强的建筑材料和高效的结构体系。于是,在屋盖质量得到有效降低的同时,结构刚度也日趋变柔。因此,风荷载已成为这一类结构的主要控制荷载[2,3]。目前在实际工程中,很多大跨结构的抗风设计仍在套用高层、高耸结构的设计方法。尽管经过半个多世纪的发展,在Davenport、Simiu、Scanlan等一批结构风工程学者的努力下,高层、高耸、桥梁结构的抗风设计问题已相对得到了较好的解决,但将其沿用至大跨结构的抗风设计,还面临许多新的问题[4,5]:(1)风荷载时空特性复杂。对于大跨结构,屋面大部分处于气流的分离和再附区域,由结构自身引起的特征湍流可能对屋面风荷载起主要控制作用。(2)结构风振响应分析中需考虑多阶振型的影响。大跨屋盖结构的风振响应常常有多阶振型参与,且可能存在一些高阶振型对振动的贡献仍占主导地位。(3)作用的维数不同。高层、高耸这类结构大多可简化为一维的,而大跨屋盖结构的风荷载作用是三维的。因此,基于不同类型模型的风洞试验研究是目前确定这类大跨空间结构设计风荷载的主要依据。

本文针对已广泛展开的大跨空间结构屋面风荷载研究,回顾了几类空间结构典型形体的风洞试验结果,总结了这几类结构屋面几何形状与风压分布之间的变化规律,并试图为这类结构抗风气动优化设计研究提供建议。文中各种典型空间结构外形尺寸如图1所示,其风向角、矢跨比、高跨比(鞍形屋盖为低点檐高与跨度之比)、长跨比、长宽比(悬挑屋盖)在本文中分别用 θ、f/D、H/D、L/D 、b/a来表示。

1 大跨空间结构典型形体风洞实验

1.1 球面屋盖

1.1.1 现有试验研究

球面屋盖的应用已有了相当长的历史。早在古罗马时期,古罗马人就运用砖石建造拱顶或穹顶,跨度达到了40多米,可以说是球面屋盖的雏形。由于其结构上的合理性及其经济上的实用性,如今球面屋盖仍被大量用于体育馆、商场等建筑,众多学者对此类结构开展了系统研究,如表1所示。

Kawamura等(1992)[7]进行了一系列试验,比较了三种不同外形和风速对风压分布的影响(f/D=0.5、H=0、β=0、f/D=1 、H=0 、β=0及f/D=0.5 、H=7.5cm 、β=29.83°；V=10m/s、15m/s、20m/s)。结果表明,对于有侧裙的模型(β≠0),模型表面风压的水平分量和竖向分量绝对值都较小,并且风压分布形状趋于简单。这说明有侧裙的穹顶圆屋盖具有很好的气动外形,可有效地减小风荷载。试验结果表明,当风速大于10m/s以后,模型表面风压受风速变化的影响很小。

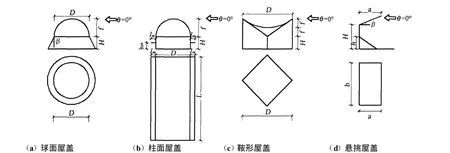
图1 典型空间结构外形尺寸Fig.1 Dimensions of typical shapes of spatial structures

表1 球面屋盖主要风洞试验Table1 Wind tunnel tests on spherical shells

Blessmann(1996)[8]给出了几个球壳屋面的实际工程风洞试验数据。作者研究了几种不同场地类型和风向角下屋面平均风压变化情况。试验结果表明,α＞0.23以后,场地类型似乎对球壳表面平均风压分布影响不大。

Hongo等(1997)[9]通过一系列风洞实验,分析了紊流及穹顶圆屋盖几何外型(包括 f/D及H/D)对平均压力和脉动压力的影响。研究表明,当风速大于7m/s时,风速对屋面风压分布的影响很小；H/D变化时对风压分布的影响远不如 f/D大,其只对局部风压的大小有一定影响,而不同的 f/D将在曲面屋盖上产生不同的气流分离模式,从而形成不同的风压分布。随着f/D的增加,屋面顶部和尾流区风吸力增大,而迎风面风吸力减小,且逐渐变为正压力。

C.W.Letchford等(2001)[11]在模拟美国规范的C类场地下,对表面粗糙和光滑的抛物形壳分别进行了风洞试验。该试验模型底部直径为480mm、高为150mm、f/D约为0.31。该试验表明,表面粗糙的壳体顶部风吸力较光滑壳体小,而尾流区的风吸力较后者大。

Blessmann(2005)[12]给出了f/D为0.5和0.25的球壳的风洞试验结果。比较发现,随着 f/D的增加,球壳迎风面正压及顶部风吸力峰值均增大。

李元齐、田村幸雄等(2005)[13]对 f/D=1/3、H=0的球壳进行了风洞实验,比较分析了不同场地类型对球壳风压分布规律的影响。试验表明,除迎风面小部分是正压外,模型表面大部分都是负压；当α＞0.2以后,场地类型似乎对球壳表面平均风压分布影响不大,这一点与Blessmann(1996)[8]的试验结果吻合。

武岳(2006)[10]给出了一个B类地貌下、H/D为1/4、f/D为1/6的球壳的风洞实验结果,可以与Hongo的实验结果作为对比。

李方慧、倪振华等(2007)[14]分析了在均匀流场、B、D类地貌下,f/D为0.1和0.2的球壳的风压分布规律,并给出了其在B类地貌下的风压系数试验结果。研究表明,f/D为0.1和0.2的球壳,其屋面几乎都处于负压作用下；前者顶部和尾流区负压均要小于后者；均匀流场和B类地貌的风压系数(参考风速为梯度风速)绝对值要明显大于D类地貌,而均匀流场的风压系数更是约为D类地貌下的2～3倍；但对于局部体型系数,由于去除了高度变化的影响,均匀流场、B、D类地貌下的局部体型系数比较接近,只在少数测点处存在差距。

1.1.2 基本结论

通过比较上述风洞试验的试验结果可以看出:

(1)f/D对球面屋盖风压分布的影响较H/D显著。从现有风洞试验数据看来,当 f/D小于0.2左右时,上述风洞试验中球面屋盖表面风压皆表现为负压,气流对屋面各区域皆产生吸力作用。随着 f/D增大,其迎风区风吸力逐渐减小,并从屋面边缘开始逐渐表现为正压；其屋盖顶部风吸力峰值及其附近尾流区风吸力均增大。当 f/D大于0.3左右时,与在屋面边缘处的迎风区一样,在屋面边缘处的尾流区也开始出现正压,这是由气流在尾流区的再附所引起的。

(2)当α大于0.2时,场地类型对球面屋盖的平均风压分布影响不大；当V大于一定值时(如7m/s[9]或10m/s[7]),其对屋面风压分布的影响可以忽略。

(3)当屋面迎风区及尾流区出现正压时,f/D应大约为0.2与0.3之间某值。但由于风洞试验数据有限,该值尚无法确认。

1.2 柱面屋盖

1.2.1 现有试验研究

柱面壳体是工程中一种常用的结构外形,被广泛用于各类大跨度空间结构。这类结构表面为曲面,风压分布及其三维空间特性较为复杂,与一般具有棱角的结构区别很大。对这种外形的结构,国内外学者已进行了较多试验研究,如表2所示。

表2 柱面屋盖主要风洞试验Table2 Wind tunnel tests on cylindrical shells

Blessmann(2003)[15]进行了一系列风洞试验来研究几何外形尺寸和墙面挑蓬几何尺寸及高度变化对柱面屋盖屋面风压分布的影响。结果表明:设置挑蓬对柱形屋面风压分布有影响,却并不十分显著。

P.A.Blackmor,E.Tsokri(2003)[16]对一系列的柱壳模型进行了大气边界层风洞实验,来研究其外形参数对屋面风压分布的影响。模型表面分区如图2所示。试验表明,a区的正压力和e+f区的吸力似乎与L/D关系不大,而a+b区和c+d区的吸力随着L/D的增加而增大。沿屋面长度方向,a+b区风压系数变化不大,而对c+d区影响明显。在离屋面端部0.1L处,其风压系数为-0.62；而在离屋面端部0.5L处,风压系数为-1.35,增大了一倍有余。这表明,从柱形屋面的端部到中部,气流由二维逐渐转变为三维。

李元齐 、Tamura Yukio等 (2006)[17]对 f/D 为1/3,L/D在1.0到3.0之间变化时的柱壳在日本规范定义的Ⅱ、Ⅲ、Ⅴ类场地下,屋面风压分布进行了研究。试验表明,L/D对柱面壳体模型表面风压的分布影响非常明显。当L/D＜3.0时,随着L/D增加,屋面风压增大；趋近3.0时,屋面风压变化不明显。

1.2.2 基本结论

上述风洞试验的试验结果表明:

(1)挑蓬的设置对柱面屋盖风压分布的影响并不十分显著。

(2)H/D对除迎风面外的屋面区域影响有限。文献[15]表明,迎风面近屋面边缘处的风压在某些几何参数下表现为负压,而文献[16]中该区域在所有几何参数下的风压均为正压。这可能是因为在屋面边缘处,气流分离严重,不同试验的结果产生较大差异。

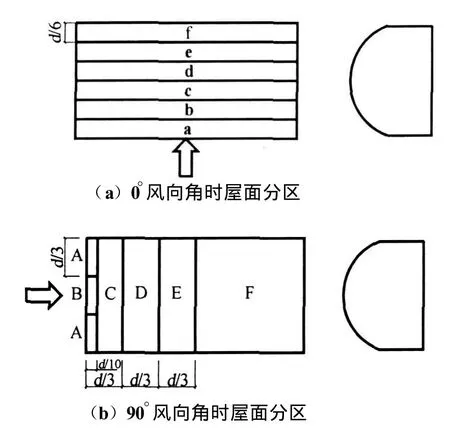
图2 试验模型以及 0°和90°风向角时屋面分区Fig.2 Wind tunnel test model and zones of roof under wind attack angle of 0°and 90°

(3)f/D对柱面屋盖的风压分布影响较大。随着f/D的增大,其迎风区的风吸力有逐渐减小且趋于正压的趋势,而屋盖顶部风吸力随f/D的增大而增加。对尾流区,当风向垂直屋脊时,文献[15]和文献[16]的试验结果所表现的变化趋势稍有不同。前者尾流区的风吸力随 f/D的增加而稍有减小,后者尾流区的风吸力则随f/D的增加而稍有增大。这可能是因为前者的试验体现了尾流区气流的再附导致风吸力减小。不论对风洞试验还是数值模拟,尾流区都是难以准确模拟的区域。

(4)L/D对柱面壳体模型表面风压的分布影响显著。当L/D小于3时,其变化对柱面屋盖表面风压分布影响较大,此时,随着L/D的增加,屋面顶部风吸力峰值增大；当L/D大于3时,气流趋于二维,此时随着L/D增加,屋面风压分布及峰值大小变化不大,其体型系数可以按我国规范的简化公式进行计算。

1.3 鞍形屋盖

1.3.1 现有试验研究

除了球形和柱形屋面,具有负高斯曲率的鞍形屋面形式也被越来越广泛地使用。国内外一些学者也对这种屋盖进行了风洞试验研究,如表3所示。下文中,0°风向角定义为沿两高点(H)吹出,90°风向角定义为沿两低点(L)吹出。

表3 鞍形屋盖主要风洞试验Table 3 Wind tunnel tests on saddle-shaped shells

A.J.Dutt(1988)[18]给出了一个 f/D为1/10、0°风向角的鞍形屋面风洞试验结果。

赵臣等(1991)[19]对 f/D 为1/10、1/12、1/16和1/20、H/D为1/5的鞍形屋面进行了风洞试验,研究了不同风向和矢跨比对鞍形屋面风压分布的影响。试验结果表明,随着 f/D减小,屋面正压区减小,其整体平均压力系数减小,并且屋面迎风前缘的风压也减小。

孙瑛(2007)[20]分别在均匀流场和B类场地下对刚性鞍形屋面进行了风洞试验,f/D选择了常用的1/12和1/8,H/D分别为1/8、1/6和1/4。试验结果表明,屋盖上风荷载仍是以风吸力为主,且最大风吸力主要分布在迎风侧的边缘或拐角区域。与文献[19]不同的是,其屋面迎风前缘的风压随 f/D的增加而减小。此外,鞍形屋面风压系数在均匀流场和B类场地下相差不大。

1.3.2 基本结论

根据上述风洞试验的试验结果,可以看出:

(1)鞍形屋盖上的风压仍主要表现为风吸力。对0°风向角(风沿两高点吹出),屋面迎风前缘风吸力最大,此后沿两高点连线逐渐降低；对90°风向角(风沿两低点吹出),屋面迎风前缘风吸力最小。而风吸力峰值发生在屋面中心正曲率顶点处,因为气流在此处发生了分离；对45°风向角而言,屋面迎风前缘风吸力最大,且风吸力峰值发生在屋面边缘靠低点一侧。

(2)f/D对鞍形屋盖风压分布影响显著。从现有试验数据看来,随 f/D的增加,鞍形屋盖风压分布形式基本一致,并且屋面将出现正压区,然而迎风前缘风压随f/D变化规律有待利用CFD进一步研究。

1.4 悬挑屋盖

1.4.1 现有试验研究

对于整体敞开体型的大跨度屋面,目前主要被用作体育场的看台挑篷,这种结构上下表面均受到风作用,风荷载为上下表面风压的叠加(净压)。国内外一些学者对这种屋盖进行了风洞试验研究,如表4所示。

表4 悬挑屋盖主要风洞试验Table 4 Wind tunnel tests on cantilevered roofs

LAM K M,A.P.To(1995)[21]给出了一个b/a为6.6∶1的悬挑屋面风洞试验结果(净压)。试验表明,对水平悬挑屋盖,气流在迎风面前缘分离,且在尾流区可能发生再附,出现小范围正压θ=0°时风吸力区域最大,且沿风向逐渐减小；θ=90°时风压最小。

LAM K M,ZHAO JG(2002)[22]给出了一个悬挑屋面风洞试验结果。模型几何尺寸为:β=0°、b×a=78m×15m、H=18m、h=13.5m。试验结果表明,无论是风压峰值还是分布形式,屋面净压受上表面风压影响更大；屋面风压受风向角影响显著,但当θ＜90°时,其影响相对较小,屋面净压峰值及分布形式变化不大。θ=60°时,在迎风区一侧出现小片正压区。θ=90°时,全屋面风压都较小。θ＞90°时,由于看台的阻挡,下表面正压减小,且开始出现负值。θ=180°时屋面风压分布与θ=0°十分类似,只是风压峰值较后者略小。

ZHAO JG,LAM K M(2002)[23]进行了一系列风洞试验来研究悬挑屋盖倾角对屋面风压分布的影响。试验模型几何尺寸为 :β=-5°、5°、10°；b×a=78m×15m ；H=18m ；h=13.5m 。研究表明,β=-5°和 0°时,无论是风压峰值还是分布形式二者十分相似。以θ=0°为例,当 β由-5°变为 5°和 10°时 ,屋面迎风前缘的带状等压线逐渐变为沿两端分布的局部高风吸力区域,而在屋面中部,产生高风吸力的气流分离区不再出现；β变化时,下表面风压变化不大,这说明相对与屋面倾角而言,正面看台对下表面风压分布影响更大；β=-5°和 0°时 ,屋面迎风前缘风压系数比 β=5°和10°时稍大,这是因为气流在上表面分离时,前者产生的风吸力较后者大；随着 β从-5°增加到 10°,屋面整体风吸力增加,且当风向角为120°左右时出现正压。当β大于5°时,整体风吸力变化不大。

A.Katsumura,Y.Tamura等(2007)[24]给出了一个悬挑屋面风洞试验结果。其试验模型几何尺寸为 :β=5°、b×a=96m ×72m 、H=72m 、h=0m 。 可以看到θ=0°时,最大风吸力发生在迎风面前缘。沿风向屋面风压逐渐减小,且在尾流区出现了小范围正压。

1.4.2 基本结论

根据上述风洞试验的试验结果,可以看出:

(1)悬挑屋盖上的净压主要表现为风吸力；上表面一般为吸力,下表面一般为压力；设置正面看台可以增加屋盖下表面压力,这是因为其可以极大地改变气流在屋盖下方的分离形式。

(2)屋面净压峰值及分布形式受屋盖上表面风压的影响较大。

(3) 屋盖倾角对屋面风压分布影响较大,这是因为其可以改变气流在迎风面前缘的分离形式。从现有风洞试验数据看来,随着β从-5°增加到 10°,屋面整体风吸力增加；当β大于5°时,整体风吸力变化不大。

2 结论与展望

本文较系统地总结、回顾了大跨度空间结构几种典型形体表面风压分布的现有风洞试验研究成果。可以看出,本文针对的几种典型形体表面风压分布规律受其形状比例参数变化的影响很大,而针对这种变化规律的研究可以用于这类形体的大跨空间结构的抗风气动优化设计,从而有效减少结构表面的局部或整体最大/小风力作用。

另一方面,到目前为止,限于风洞试验本身的局限性,即使对于上述几类较典型的大跨屋盖形式,尚不能对其屋面风荷载以及几何参数对风压分布变化规律的影响进行较系统的研究。随着CFD技术的发展,目前可以对一些相对简单的典型形体进行风压分布特性的数值模拟,得到的平均风压分布系数与风洞试验结果相比较为吻合[25-28],但CFD数值模拟的结果基本上只能针对平均风压分布,同时对复杂体形的建筑表面风压分布模拟仍值得进一步研究。尽管如此,针对上述几类较典型的简单大跨屋盖形式,完全可以利用CFD数值模拟技术进行几何参数对风压分布的影响分析,结合已有的风洞试验数据,可以展开典型大跨屋盖形式气动形态优化及效果研究,以此进一步提出这类结构外形的气动优化设计原则,供初步设计参考。

致谢:本文得到了国家自然科学基金重点项目(No.50638050)及东南大学混凝土及预应力混凝土结构教育部重点实验室高等学校实验室访问学者基金的资助,在此谨致谢意!

[1]沈世钊.大跨空间结构的发展-回顾与展望[J].土木工程学报,1998,31(3):5-14.

[2]YASUSHI UEMATSU,KEISUKEWATANABE,etc.Wind-induced dynamic response and resultant load estimation of a circular flat roof[J].J.of Wind Eng.and Ind.Aerodyn,1999,83:251-261.

[3]YASUI H,MARUKAWA H,etc.Study of wind-induced response of long-span structure[J].J.of Wind Eng.and Ind.Aerod yn.,1999,83:277-288.

[4]陈波.大跨度屋盖结构等效静风荷载精细化理论研究[D].哈尔滨工业大学,2006.

[5]李元齐.大跨度空间结构风荷载模拟技术研究及程序编制[J].空间结构,2001,7(3):3-11.

[6]BIGGS D W,PETERKA J A.Aerodynamics model tests of tall buildings[J].ASCE J.Eng.Mech.,1989,115:618-635.

[7]SUMIO KAWAMURA,TATSUHIKO KIUCHI,etc.Characteristics of wind pressure actiong on spatial large dome[J].J.of Wind Eng.and Ind.Aerodyn.,1992,41-44:1511-1512.

[8]BLESSMANN J.Researches on wind effects on domes in Brazil[J].J.of Wind Eng.and Ind.Aerodyn.,1996,65:167-177.

[9]YASUSHI UEMATSU,MOTOHIKO YAMADA,etc.Wind loads and wind-induced dynamic behavior of a single-layer latticed dome[J].J.of Wind Eng.and Ind.Aerodyn.,1997,66:227-248.

[10]武岳.大跨屋盖结构的风效应及抗风设计理论研究[D].同济大学,2006.

[11]LETCHFORD C W,SARKAR PP.Mean and fluctuating wind loads on rough and smooth parabolic domes[J].J.of Wind Eng.and Ind.Aerod yn.,2000,88:101-117.

[12]BLESSMANN.Aerodynamic studies for the Brazilian wind code[A].The 10thAmericas conference on Wind Engineering[C].2005.

[13]李元齐,田村幸雄,沈祖炎.球面壳体表面风压分布特性风洞实验研究[J].建筑结构学报,2005,26(5):104-111.

[14]李方慧,倪振华,沈世钊.不同地貌下几个典型屋盖的风压特性[J].建筑结构学报,2007,28(1):119-124.

[15]PALUCH M J,LOREDO-SOUZA A M,BLESSMANN J.Wind loads on attached canopies and their effect on the pressure distribution over arch-roof industrial buildings[J].J.of Wind Eng.and Ind.Aerodyn.,2003,91:975-994.

[16]BLACKMORE P A,TSOKRI E.Wind loads on curved roofs[J].J.of Wind Eng.and Ind.Aerodyn.,2006,94:833-844.

[17]李元齐,TAMURA YUKIO,沈祖炎.柱面壳体表面风压分布特性风洞试验研究[J].同济大学学报,2006,34(11):1457-1463.

[18]DUTT A J.Wind pressure distribution on a multiple hyperbolic parabolic shell roof building[J].J.Space Structures,1986,1:225-230.

[19]赵臣,陆钦年,沈世钊.双曲抛物面鞍形屋面风压分布的实验研究[J].哈尔滨建筑工程学院学报,1991,24(1):29-36.

[20]孙瑛.大跨屋盖结构风荷载特性研究[D],哈尔滨工业大学,2007.

[21]LAM K M,TO A P.Generation of wind loads on a horizontal grandstand roof of large aspect ratio[J].J.of Wind Eng.and Ind.Aerodyn.,1995,54/55:345-357.

[22]LAM K M,ZHAO J G.Occurrence of peak lifting actions on a large horizontal cantilevered roof[J].J.of Wind Eng.and Ind.Aerod yn.,2002,90:897-940.

[23]ZHAO J G,LAM K M.Characteristics of wind pressures on large cantilevered roof s:effect of roof inclination[J].J.of Wind Eng.and Ind.Aerodyn.,2002,90:1867-1880.

[24]KATSUMURA A,TAMURA Y,NAKAMURA O.Universal wind load distribution simultaneously repro-ducing largest load effects in all subject members on large-span cantilevered roof[J].J.of Wind Eng.and Ind.Aerodyn.,2007,95:1145-1165.

[25]李华锋,马骏等.空间结构风场风载的数值模拟[J].上海交通大学学报,2006,40(12):2112-2117.

[26]汪丛军,黄本才等.环状悬挑屋盖平均风压与风环境数值模拟[J].同济大学学报,2006,34(6):711-715.

[27]孙晓颖,武岳等.鞍形屋盖平均风压分布特性的数值模拟研究[J].工程力学,2006,23(10):7-14.

[28]晏琴.CFD技术在大跨度空间结构风场数值模拟中的应用[D].同济大学,2006.