递归投影方法(RPM)及其在流场数值模拟中的加速收敛性能研究
李孝伟,王正裕
(上海大学,上海市应用数学和力学研究所,上海200072)
0 引 言
计算流体力学的发展过程是一个流体动力学模型的精确化和细致化的过程,同时流场数值模拟的收敛性和计算效率也成为了计算流体力学中的关键问题。为了提高计算效率,广大计算流体力学工作者发展了多种加速收敛的措施,典型的如采用当地时间步长和隐式残值光顺技术等。但人们并不满足,因为现实期待一些更为有效的加速收敛方法的出现。
1993年,G.M.Shroff与H.B.Keller[1]提出一种递归投影算法(the Recursive Projection Method,RPM),目的是为了稳定和加速非线性分叉和混沌的数值研究中的迭代过程。对于离散的偏微分方程,该方法对迭代变量的残差构造Krylov子空间,并从中分离出影响迭代收敛的强势特征子空间,进而通过使用牛顿迭代法消除其对迭代收敛进程带来的负面影响。
1999年,Philip Love[2]在三维的Kolmogorov流动和泰勒涡流的分叉研究中应用了 RPM方法来加快定位流场的分叉点,以探讨湍流的起源过程。在该研究中,作者证明了RPM方法可以有效地帮助加快发现低雷诺数下 Kolmogorov流动的分叉现象。2001年,为了提高RPM方法对于不变子空间的近似精度,V.Janovsky和Liberda.Praha[3]提出一种改进的RPM方法。该方法使用Cayley变形处理雅可比矩阵,以修正超出稳定边界特征值所对应的子空间的正交基;在得到的修正的正交基上,提出一种耦合的双重迭代的 RPM方法,最后证明该修正的RPM方法的能够发现一些原始RPM方法发现不了的Hopf分叉点。2005年,M.Dorobantu和J.Möller将RPM用于计算流体力学的NSMB程序块中作为加速数值收敛进程的外壳[4-7],计算了二维超音速喷管流动和二维亚音速翼型绕流,并证明RPM方法在二维定常流场的计算中可以达到约5倍的加速效果。
从以上研究者们的结果可以看出,RPM方法的加速收敛效果和作用非常显著,这激发了本文作者对它的研究兴趣。在研究中发现,原有RPM方法在实施过程中不易保证正交基的精度,针对此,本文提出了一种改型的RPM方法。计算实践表明,该改型的RPM方法,不仅可以更好地保证正交基的精度,还可以节省相关的计算时间。文中一方面还研究了几个重要参数对RPM方法加速收敛性能的影响规律,另一方面还研究了在流场数值模拟中采用了常规的加速收敛措施以后改型的RPM方法的加速收敛性能。
1 RPM方法
对于存在定常解的偏微分方程(组),数值求解时一般是通过空间离散,构造一个包含时间导数项的常微分方程(组)来进行求解,可以表示为

在时间推进上,可以使用一个迭代格式来表述方程(1)的求解过程,

令Fy为由离散的方程组所定义的雅克比矩阵。假设对于迭代格式(2)式,存在解y*=F(y*),则雅克比矩阵可表达为

从而,(2)式的收敛特性就由雅克比矩阵J的特征值的谱分布来决定。如果该矩阵的所有的特征值的模都小于1,那么(2)式将渐进地收敛到y*;当J有一小部分特征值的模小于1但非常地接近于1时,迭代式(2)的收敛进程会变得非常的缓慢;如果J存在任意一个特征值的模大于1,那么(2)式的迭代格式就会发散。对于模接近1或大于1的J的特征值,由于它们是影响离散方程(2)式收敛的强势因子,所以称之为J的强势特征值。
为了稳定形如(2)式的收敛缓慢或不稳定的迭代格式,G.M.Shroff和H.B.Keller[1]1993年提出了RPM方法。RPM方法的主要思想是,通过分离出雅可比矩阵J的强势特征值所决定的不变子空间,进而使用牛顿迭代法在该子空间中消除强势特征值对收敛进程所带来的负面影响。
假设式(2)的雅可比矩阵J存在小部分的特征值位于区域Kδ={(|z|≤1-δ} (δ>0)之外,即有如下形式,|λ1|≥|λ2|≥… ≥|λp|>1-δ≥|λp+1|≥…≥|λN|,(其中p≪N)。对应于以上特征值的分布,定义子空间P和Q如下:
P≡对应于特征值{λ1,…,λp}的 F*y的最大不变子空间;
Q≡RN-P,为P的正交补。
对于所定义的子空间,通过对特征值{λ1,…,λp}的分离和提取,可以构造一组对应的不变子空间P的正交基Vp,进而在Vp的基础上构造正交投影算子P和Q。
通过向两个正交子空间的投影,方程的解也就分解成为了如下两部分,

其中,对应于构造的不变子空间的正交基Vp,投影算子可表达为,

将(5)式应用到(4)式有

由于不变子空间P是分离出来的影响收敛进程的强势特征子空间,对应于该空间的投影分量pn是收敛缓慢或发散的解分量。为了对其收敛特性做相应的改善,把牛顿方法

应用到(6a)式,从而得到如下的RPM 方法的迭代形式,

若设Δqn=qn-q*,将解 qn+1在 y*=p*+q*处泰勒展开可得,

可以证明[4],上式中g*q=QJ*Q的所有特征值位于Kδ的邻域内,并且QJ*P=0。因此,在以上分解的迭代关系中,RPM方法首先通过递归地对投影分量qn的残值Δqn进行监控而得到补空间的迭代特性变化,并从中构造和抽取Jn的强势特征值所对应的不变子空间的正交基Vp,进而相应地对迭代格式进行投影改进。这也是“递归”和“投影”(Recursive&Projection)所表述的意义。
对于(8a)式中出现的Jn,我们并不需要显式地直接求取,在所构造的正交基Vp的基础上,通过对(3)式构造差分格式,可以直接得到

其中,vj为Vp的列向量;ε为大于0的小量,一般可以取为10-8~10-12。通过差分格式非显式地求取离散方程的雅可比矩阵也是RPM方法的能够实现以小的计算代价而获得良好的加速效果的重要原因之一。
至于求取投影算子P和Q的递归算法,包括基于累积方式的正交基的计算、正交基的精度的维持等,请参见文献[1],在此不再重述。下面仅叙述一下RPM 方法对“正交基维数的减小”的处理
RPM方法在递归求取不变子空间的正交基的过程中,检测的是n时刻的雅可比矩阵的变化。随着计算进程的发展,Jn是与n时刻计算所得到的流场变量yn相关的,因此Jn的强势特征值也应该是随着计算进程不断变化的。所以,前面所积累的不变子空间P也就可能无法近似为当前时刻的雅可比矩阵的优势特征子空间,其正交基会变得不准确。这进而会导致整个计算的发散和失败。对此,G.M.Shroff和H.B.Keller在文献[1]中提出需要在适当的时刻减小不变子空间的基,其思想如下。
基于已有的强势特征子空间的正交基Vp,有

可以证明矩阵H-的特征值为的特征值的一个子集,并为不变子空间P部分对应的特征值。理论上RPM方法只需要对大小为m×m的矩阵的特征值进行重选,淘汰置于Kδ区域内的特征值,并求得剩余特征值所对应的基矢量就可以了。但是我们在具体实施的过程中发现,对矩阵的特征值进行重选不难,但是对重选后得到的复数特征值对所对应的不变子空间的正交基的构造存在困难。对于重选后的矩阵的复数特征值对,其所对应的特征向量也是复数形式。在此,问题的困难在于如何结合已有的正交基组和复数特征向量组构造新的正交基组。也就是说,我们在将一个酉空间的基矢量转化成单个的实空间的基矢量时找不到相关的理论依据。H.B.Keller提出,将矩阵的复特征向量分解为由复数的实部和虚部分别构造的两个实向量来处理。但是,对于这种处理方法,在计算时如果淘汰的特征值少于复特征值的数量时,我们原意是要减小和筛选原不变子空间的正交基,就有可能变为增加原不变子空间的正交基。在数值试验中,我们发现,这种处理方法很难保证正交基V p的计算精度和合理性,并会导致计算的失败。为此,我们发展了一种更容易保持正交基V p精度的改型的RPM方法。
2 改型的RPM方法
在原RPM过程中,Vp的精度难以保持的最根本原因在于这种累积计算正交基的方式会使得早被计入的一些正交基过时,因而积累的正交基不能实时地反映当前雅可比矩阵Jn的变化。如果要保持正交基Vp的精度,就需要在某些时候减小正交基Vp的维数,也就是需要剔除掉一些过时的正交基。但是,这样的处理方式又会使算法变得非常复杂而不易于实现。为此,我们在流场计算的过程中考虑放弃这种累积计算正交基的Vp方式,而采用即时覆盖的方式计算正交基Vp。
鉴于对所采用的计算正交基Vp的方式的改变,我们对解的投影分量qn的收敛速度的监视也应该相应地改变为对解的整体收敛历程的监视:通过监视Δyn+1=yn+1-yn的变化,实时地求取全局的收敛缓慢的强势特征子空间的基,以覆盖原有的基Vp,即在每次RPM迭代之后,我们得到新的yn+1,计算

并将得到的Δyn+1累积到Krylov向量组中,

对Krylov向量组采用QR分解并提取满足Ka接受比条件的基Vp,覆盖原有的正交基Vp,进而进入新一轮的RPM数值迭代。
本文在采用覆盖的方式计算正交基Vp时,首先使用已有的正交基Vp,按(8)式对迭代进行加速计算,当累积了 ks组的 Δyn后,对由 Δyn构造的 Krylov向量组求取新的正交基Vp,并覆盖已有的正交基Vp,再重复(8)式的数值迭代。这种以覆盖方式计算正交基Vp的RPM方法,不仅可以更好地保证正交基Vp的精度,还可以节省原RPM方法中维持基的精度和减小基的维数的相关计算。
本文后面部分提到的RPM方法均指的是该改型的RPM方法。
3 几个参数的影响
给出方程:
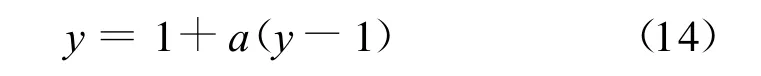
可以看出,以上方程的解析解为y*=1且与a的取值无关。对方程(14)构造迭代格式

通过前面的描述可以知道,当存在某个a(i)的绝对值趋近于1时,它所对应的y(i)值会很缓慢地收敛于y=1。取空间离散点数N=31,y0(i)=5.0,a(i)=0.1+0.89×i/N,i=1,2,…,N。可以看出,有7个特征值大于0.80,有4个特征值大于0.90。
加入 RPM方法,程序中设定以下参数:Ka:Krylov接受比;ε:计算 Jnvj时的小量 ;Nstep:使用迭代格式,每计算 Nstep步y 值,计算一次 Δyi;Ks:Krylov向量组的大小。
分别检测了以上参数对RPM数值迭代效果的影响。收敛标准统一采用Ry<10-10。计算结果见表1~表4。从表中可以看出:(1)Ka的取值大小对RPM的收敛效果存在明显的影响:Ka越大,发现和提取第一组不变子空间正交基的时间越迟,该组正交基的维数也相对偏小;(2)ε对发现正交基的时间以及正交基的维数没有显著的影响;(3)在具有静态的特征值数值试验中,Nstep的取值极大地影响着RPM的加速收敛效果,高频率地求取Δyi可以相对快速地发现强势特征值所对应的不变子空间,从而以相对较小的总迭代次数达到收敛标准;(4)Ks对RPM迭代的收敛效果不具有明显的影响,对强势特征值所对应的不变子空间的正交基的添加数目也没有明显的影响。
以上结果说明,对于收敛缓慢的数值迭代格式,RPM方法具有非常明显的加速收敛效果;而对RPM方法的效果影响较明显的参数有Ka和Nstep。在所构造的简单模型中,RPM方法的加速最佳效果达到70倍。

表1 Ka对RPM数值过程的影响Table1 Effect of Ka on the process of RPM

表2 ε对RPM数值过程的影响Table 2 Effect ofεon the process of RPM

表3 Nstep对RPM数值过程的影响Table 3 Effect of Nstep on the process of RPM

表4 Ks对RPM数值过程的影响Table 4 Effect of Ks on the process of RPM
4 RPM方法流场数值模拟中的加速收敛效果
本节数值模拟了二维翼型绕流。流场控制方程采用Navier-Stokes方程。数值离散时,采用中心有限体积格式进行空间离散,在时间上采用混合五步Runge-Kutta格式加以求解。
本节的主要目的是想知道,在一般的流场解算器中加入了常规的加速收敛措施以后,再应用RPM方法,流场计算的收敛性能是怎么样的。所以,在流场解算器中我们首先加入了当地时间步长和隐式残值光顺等加速收敛措施,然后再运用RPM方法。由于Nstep的取值与当地时间步长的计算频率相关,此处选取最小取值5。Ks取值为10,ε取为1E-12。
以NACA0012翼型为研究对象,来流状态为Ma=0.7584,α=0.0°,Re=9.0×106。
图1展示了加入RPM方法之后数值模拟所得到的翼型表面压力分布,并与试验数据[8]进行了对比;图2为有加入RPM 方法(考虑了多个Krylov接受比Ka取值)和没有加入RPM方法分别计算得到的残差收敛过程的对比。
从图1、图2中可以看出,在翼型绕流的数值模拟程序中加入RPM方法所得到的计算结果与试验结果符合得很好,这也证明,RPM方法对数值过程没有产生负面的影响;RPM方法对流场数值计算有明显的加速收敛效果,即使在流场解算器中加入了当地时间步长和隐式残值光顺来加速收敛措施的情况下,也能使总体收敛速度提高近1/3。但在残差的收敛过程中,相对于原有的数值计算程序的收敛进程,采用RPM方法的残差收敛曲线存在相对明显的数值震荡。这主要是由于在翼型绕流的计算时采用了当地时间步长的缘故。不同网格点的时间步长是不一样的,甚至同一网格点在不同迭代步其时间步长也是改变的,而RPM思想是通过监视在前面的迭代步的残差变化递归地发现和分离强势特征子空间,因此,RPM方法递归的正交基提取方式不能很好地反映当前迭代步的时间步长所影响的离散雅可比矩阵的不变子空间。

图1 翼型表面压力Fig.1 Pressure distribution of the NACA0012 airfoil

图2 残值收敛曲线Fig.2 The curves of residual convergence
5 结 论
通过以上研究,可以得出如下几点结论:
(1)改型的 RPM方法,不仅可以更好地保证正交基的精度,还可以节省相关的计算时间。
(2)静态特征值的数值试验表明,Ks和Nstep是影响RPM方法的加速收敛效果的两个主要因素,其他因素的影响相对很小。Ka越大,发现和提取第一组不变子空间正交基的时间越迟,该组正交基的维数也相对偏小。Nstep值相对越小,可以相对快速地发现强势特征值所对应的不变子空间,从而以相对较小的总迭代次数达到收敛标准。
(3)在流场数值模拟中即使采用了常规的加速收敛措施以后,再使用RPM方法同样可以使收敛速度提高近1/3,说明RPM方法在加速收敛方面具有很大的发展潜力。
[1]SHROFF G M,KELLER H B.Stablization of unstable procedures:the recursive projection method[J].Siam J.Numer.Annal,1993,30(4):1099-1120.
[2]PHILIP L.Bifurcations in Kolmogorov and Taylor-voertex flows[D].[Doctor Thesis].California:California Institute of Technology,1999.
[3]JANOVSKY V,LIBERDA O,PRAHA.Continueation of invariant subspacevia the recursive projection method[J].Ap plications of Mathematics,2003,48(4):241-255.
[4]DOROBANTU M,MÖLLER J.RPM acceleration of the NSMB compressible flow code[R].TRITA-NA-0118,Royal Institute of Technology,Stockholm,Sweden,2001.
[5]MÖLLER J.Aspects of the recursive projection method applied to flow calculations[D].[Doctor Thesis].Sweden Royal Institute of Technology,2005.
[6]STEFAN G,MÖLLER J.Recursive projection method for efficient unsteady CFD simulations[A].In:24th-European Congress on Computational Methods in Applied Sciences and Engineering[C].2004.
[7]MÖLLER J.An investigation of the recursive projection method on a scalar linear and non-linear partial differential equation[R].TRITA-NA-0118,Royal Institute of Technology,Stockholm,Sweden,2001.
[8]LADSON C L,HILL A S,JOHNSON W G.Pressure distributions from high Reynolds number transonic test of an NACA 0012 airfoil in the langley 0.3-meter transonic cryogenic tunnnel[R].NASA TM 100526,1987.

