用湍流模型研究Richtmyer-Meshkov不稳定性诱导的湍流混合

杨 玟,王丽丽 ,张树道 ,何长江,杭义洪

(北京应用物理与计算数学研究所,北京100094)

0 引 言

界面不稳定性的发展及其引起的湍流混合在各种背景下都可能遇到,如燃烧、旋转机械、惯性约束聚变(ICF)、超新星爆炸和地球物理学。很多国家都在该领域开展了大量的研究,如美国的三大武器物理实验室(LANL、LLNL和 SNL)、英国核武器研究院(AWE)、法国原子能委员会(CEA)等[1-3]。目前,随着计算机技术的迅猛发展,界面不稳定性的高精度高分辨率数值模拟(如直接模拟DNS、大涡模拟LES)[12,14]已成为该领域研究的重要手段之一,它为揭示界面不稳定性发展的内在规律发挥了一定的作用。但是,由于界面不稳定性现象以及与其相关物理过程的复杂性,高精度计算不仅费时,而且,受计算机硬件条件限制,其模拟能力目前尚不能解决许多复杂的实际应用问题。因此,界面不稳定性诱导湍流混合的雷诺平均方法(RANS),即湍流模型研究近年来受到了越来越多的关注[4-6]。国内在这方面与国外的差距较大,至今尚未见相关的报导。

当激波加速两种不同密度流体间扰动界面时产生Richtmyer-Meshkov不稳定性(RMI)。这种不稳定性理论上由 Richtmyer(1960)发现并描述[7],由Meshkov(1969)从实验中证实[8]。它是分层流体湍流混合的典型机制,对ICF是相当重要的。ICF中包含氘氚燃料的小靶丸被激光产生的冲击波压缩,其目的是在被压缩的ICF靶丸内部获得足够高的压力和温度来点燃燃料。外壳和内部燃料间界面上不稳定性产生的混合抑制聚变反应,可能是能量产出的一个限制因素。

RMI通常在激波管中被研究。几乎在所有激波管实验中,重流体和轻流体初始采用塑料薄膜分隔,它通常被直接置于薄丝网下面。当激波经过丝网时将薄膜分裂成碎片。激波管实验大多提供湍流混合区宽度的纹影图以及采用X射线、红外吸收或反射和微分干涉测量法得到的平均密度。这些诊断仅给出湍流的间接测量:混合的增强或平均密度脉动的增强。法国原子能委员会的F.Poggi等[13]首次采用激光多普勒测速仪(LDA)测量了激波管中产生于冲击波的气相混合物的瞬态速度,给出了混合区与反射激波相互作用前后混合区速度脉动的发展。这些实验第一次给出了湍流的直接测量,为校核湍流混合模型提供了重要数据。

G.Dimonte[6]发展了描述界面不稳定性诱导湍流混合自相似增长的k-L模型,其中湍动能产生项以简单的浮阻力模型[4]为基础来构造。多相流模型[5]具有显著优于单相模型的特点是能够描述分离,但这类模型复杂、数值上强度大,且有时不稳定。湍流模型应用于不稳定性时,必须面对如下一些困难:(1)需要给出初始湍流状态；(2)当模拟湍流与激波相互作用时,为了抹掉激波和消除梯度,强烈的不连续性的数值处理需要数值耗散,使得它们在产生湍动能上人为地效率降低；(3)n阶关联弱依赖于(n-1)阶关联的封闭假设在激波的作用下不再有效；(4)封闭假设无法考虑不均匀性。针对上述难点,本文将一般工程应用中被广泛采用的k-ε模型运用到不稳定性诱导湍流混合的研究中。

1 模型方程和数值方法

模型以N-S方程为基础,但是包含依赖于湍动能k和耗散率ε的湍流粘性μT。流动参数,除压力和密度采用系综平均之外,其它都采用质量加权平均,即Favre平均。例如,速度可分解为平均分量和脉动分量,即 u=+,将它们代入到流动方程中。对方程取平均,可得到平均和脉动分量各自的演化方程。对于可压流动,Favre平均以密度加权以致于最终的方程为复杂性渐增的所有阶的平均流动的展开式[9]。但是,展开式必须以一组简单的封闭假设结束。所求解的方程为:

上述方程中雷诺应力τij和湍动能产生项-需要进行封闭。通常雷诺应力采用平均速度来构造,冲击存在时,尤其是加密网格时,具有梯度乘积的项可能变得不稳定,到目前为止,还未得到激波存在时保持可实现性约束(realizability constraints)的湍流剪切应力的形式。与G.Dimonte等[6]采用的省略偏应力张量的方法不同,本文采用施加通量限制器的方法来排除存在激波时可能会出现的很大的非物理值,即根据量纲分析和 RMI产生的特点(冲击波作用于不同密度流体间界面),湍动能产生项的计算定义为:

求解的程序中采用具有总变差递减(Total Variation Diminishing,简称 TVD)保持性质的三阶Runge-Kutta方法进行时间积分[10]:

对流项采用高阶WENO方法重构网格边界的通量,扩散项采用交替方向隐式迭代(ADI)法求解。

由于k-ε模型在工程中被广泛应用,模型中的常数已经过仔细地研究而被确定,即所有常数通过数值实验或与不可压流体中进行的典型实验比较来确定。新的常数 λm,λM,Cε0和 σρ根据激波管实验标定 。本文中模型常数的选取为:CD=0.09,λm=0.1,λM=1.25,σe=0.9,σc=1.0,σk=0.87,σε=1.3,σρ=0.3,Cε0=1.06,Cε1=1.47,Cε2=1.90,Cε3=0,αρ=0.67 。

充分发展湍流的统计模型大多用于定常流动,其中初始条件仅承受数值约束。实际上,为了达到收敛和最小化计算花费,初始条件选得与想要得到的解尽可能接近。在非定常问题中情况很不一样。因为封闭模型不计算不稳定性的初始阶段,湍流状态必须采用现象学原则和可得到的实验数据来初始化。换句话说,为了采用相应平均量的第一梯度定理来封闭湍流通量,已假设充分湍流状态。混合区湍动能的初始分布取为高度为kinit(=0.0028U)的三角形,耗散率的初值分布为εinit=0.164k/Linit,其中UI为激波经过后界面的运动速度,Linit为模型开启时刻混合区宽度。

2 结果分析与讨论

采用上述模型对Andronov等的激波管实验[11]进行了模拟。在Andronov实验中,分隔空气和氦气的有机薄膜位于距离管右端16.9cm处,Atwood数(A=(ρ2-ρ1)/(ρ2+ρ1))为0.75。马赫数为1.3 的激波产生于管左侧的空气中,激波向右运动。计算域取为53.6cm×5cm。界面初始扰动由 ζ(y)=arcos给出。系数ar从一高斯分布中选取,W为y方向宽度,初始扰动中存在的波长范围为0.25cm～1cm,扰动振幅被归一化来使扰动标准差/2等于0.02cm。计算中界面在t=0.76ms时刻被加速,k-ε模型在t=0.8ms时打开(数值实验发现模型打开时间的变化(t=0.9ms)对结果影响不大)。

图1 空气/氦气湍流混合区宽度和轨迹随时间的变化Fig.1 Widths and trajectory of Air/He turbulent mixing zone at different times

图1给出了混合区宽度以及混合区边界随时间的变化曲线。从图中可见,这些宏观量的计算值与实验值基本吻合,误差在10%之内。虽然后期混合区宽度的计算值与实验值吻合得较好,但是混合区边界都被略微低估了。这可能是由于第一次反射激波与界面相互作用后界面运动速度的误差造成的。但是,计算得到的入射激波赋予界面的运动速度为220m/s,与从冲击波关系式中得到的理论值(218.72m/s)一致。

随着计算机技术的突飞猛进,被实验验证过的直接模拟为模型的校核提供了大量有用的信息。图2给出了不同时刻混合区内空气摩尔份额沿横向的分布。由图可知,空气与氦气的相互渗透随时间逐渐增强,模型计算结果与D.L.Youngs直接模拟结果[12]吻合得很好。混合区内湍动能的分布(如图3所示)定性上是合理的,它很好地捕捉了第一次反射波到达界面时湍动能的增强。但是,由于湍动能衰减的弛豫时间远大于激波与界面的作用时间,而计算的时间还不足够长,因此图3中未呈现明显的湍流衰减。

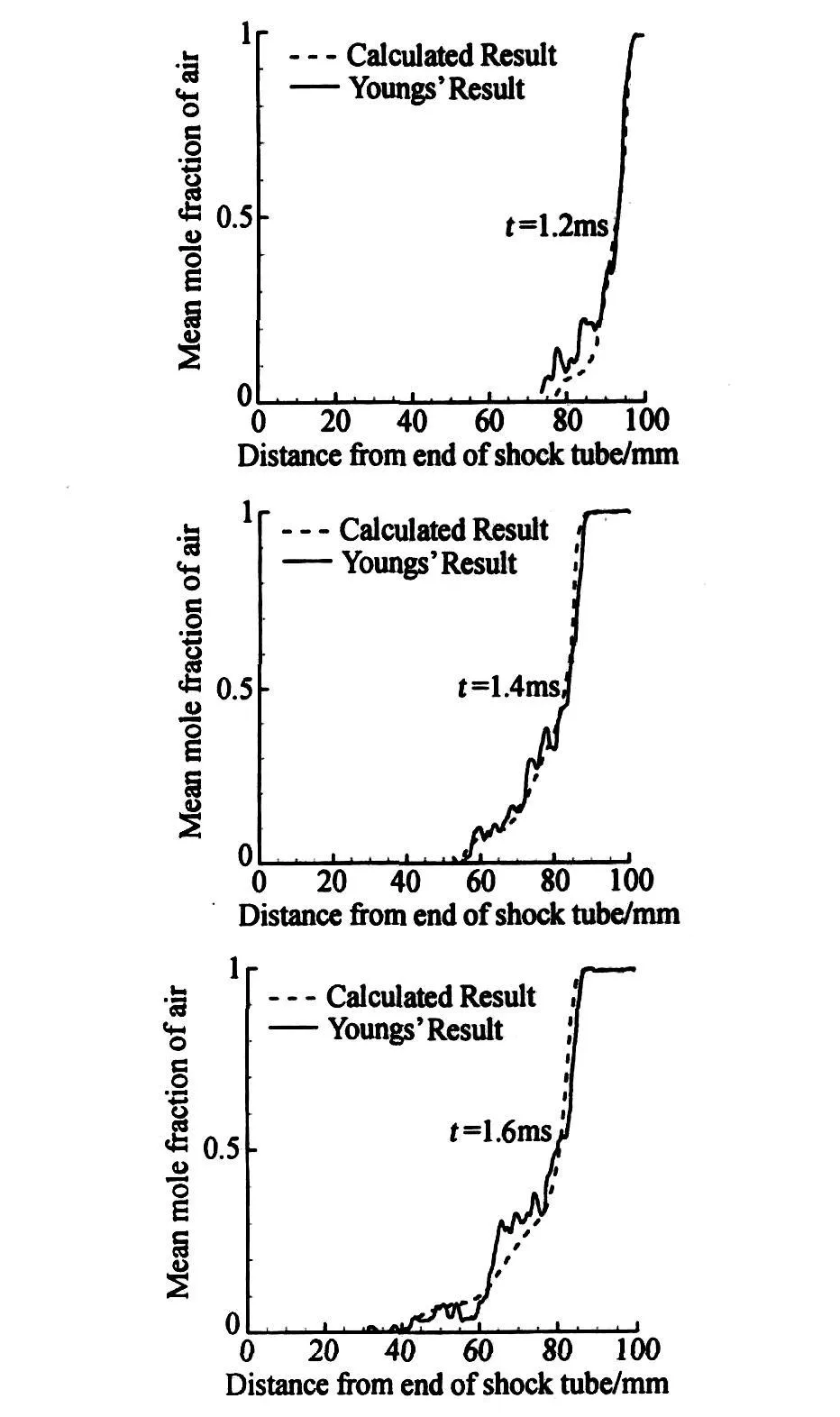
图2 不同时刻空气/氦气湍流混合区浓度沿横向的分布Fig.2 Concentration distributions of Air/He turbulent mixing zone at different times

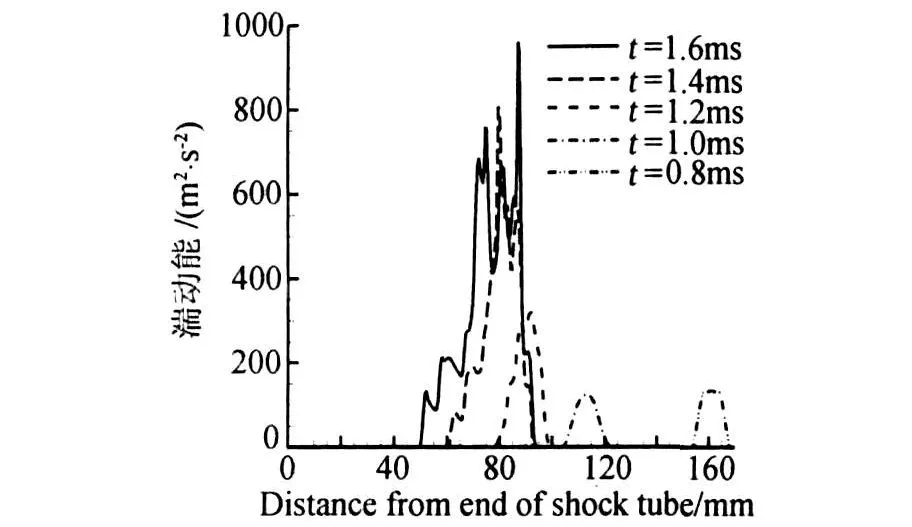
图3 空气/氦气湍流混合区湍动能沿横向的分布Fig.3 Distributions of turbulent kinetic energy of Air/Heturbulent mixing zone

正如上文中提到过的,Poggi等的激波管实验[13]首次对湍流进行了直接测量(图5(a))。该实验在横截面为8cm宽的正方形、长30cm的测试段进行。马赫数为1.45的激波入射到六氟化硫中,下游的空气由薄膜和丝网分隔(Atwood数为0.67)。计算域取为70cm×8cm。计算中初始条件的给定以实验为基础。界面初始扰动的波长取为与实验中的丝网尺寸同一量级,λ=0.05cm～0.25cm；扰动振幅没有任何实验信息,本文对所有振幅取同一个值,该值(0.02cm)由数值实验确定。

与Andronov实验的计算不同的是该模拟中t=0时刻对应于激波冲击扰动左端的时刻。图4给出了混合区宽度随时间的变化,从图中可见,不稳定性发展早期计算值与实验值吻合得较好,而后期则略低于实验值,这与直接模拟结果定性上一致[14]。

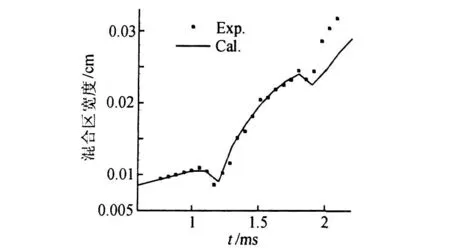
图4 六氟化硫/空气湍流混合区宽度随时间的变化Fig.4 Widths of SF6/Air turbulent mixing zone at different times

图5(c)给出了不同时刻湍动能的分布,与图5(b)的直接模拟结果[14]相比较:一方面,两者都很好地再现了第一次反射激波与湍流混合区相互作用之前湍流的衰减和它被反射激波增强的特征；另一方面,模型计算无法捕捉入射激波与界面作用时湍动能的增强,这是由于模型在入射激波经过后不稳定性发展至非线性阶段才打开。此外,模型中的湍流耗散机制似乎还需要进一步完善,因为模型计算的湍流衰减程度明显低于直接模拟的结果。

图5 六氟化硫/空气混合区湍流量的实验与模拟结果的比较Fig.5 Comparison of turbulence variants of SF6/Air mixing zonebetween experimental results and simulation results

实验结果清楚地显示了湍流的各向异性(如图5(a)所示),但是k-ε模型无法描述该现象,因此我们进一步推导了考虑密度脉动和各向异性湍流的二阶矩模型,并将它应用于不稳定性诱导湍流混合的研究中,该工作正在进行中。

3 结 论

本文将k-ε模型应用到 RMI诱导混合的研究中,经典的封闭关系采用代数关系式来补充,给出了合理描述RMI特征的湍动能产生项的表达式。采用上述模型对Andronov(1976)和Poggi(1998)的激波管实验进行了模拟,结果与实验和细观模拟(DNS)吻合得较好,并且较好地再现了第一次反射激波与湍流混合区相互作用之前湍流的衰减和它被反射激波增强的特征。这些结果表明本文采用的模型封闭、模型常数、数值算法和程序实现是合适的。此外,该工作也为不稳定性诱导湍流混合模型研究的深入打下了良好的基础。

致谢:本工作是在国家自然科学基金委员会-中国工程物理研究院联合基金“界面运动不稳定性及湍流混合研究”(No.10676005)、中国工程物理研究院科学技术发展基金“界面不稳定性诱导湍流混合的多相湍流模型研究”(课题批准号:2008B0101006)和国防科技重点实验室基金“含强间断三维多尺度复杂流场的高精度欧拉方法研究”(编号:9140C6901010702)的资助下完成的。

[1]LLOR A.Statistical hydrodynamic models for developed mixing instability flows[A].Lecture Notes in Physics[M].Springer,Heidelberg,2005.

[2]ALON U,HECHT J,OFER D,SHVART SD.Power laws and similarity of Rayleigh-Taylor and Richtmyer-Meshkov mixing fronts at all density ratios[J].Phys.Rev.Lett.,1995,74(4):534-537.

[3]CRANFILL CW.A new multifluid turbulent-mix model[R].LANL,Report LA-UR-92-2484,1992.

[4]DIMONTE G.Spanwise homogeneous buoyancy-drag model for Rayleigh-Taylor mixing and experimental evaluation[J].Phys.Plasmas,2000,7(6):2255-2269.

[5]CHEN Y,GLIMM J,SHARP DA,ZHANG Q.A twophase flow model of the Rayleigh-Taylor mixing zone[J].Phys.Fluids,1996,8(3):816-825.

[6]DIMONTEG,TIPTON R.K-L turbulence model for the self-similar growth of the Rayleigh-Taylor and Richtmyer-Meshkov instabilities[J].Phys.Fluids,2006,18:085101.

[7]RICHTMYER R D.Taylor instability in shock acceleration of compressible fluids[J].Commun.Pure Ap pl.Math.,1960,13:297-319.

[8]MESHKOV E E.Interface of two gases accelerated by a shock wave[J].Fluid Dynamics,1969,4:101.

[9]周力行.湍流两相流动与燃烧的数值模拟[M].清华大学出版社,1991.

[10]张涵信,沈孟育.计算流体力学-差分方法的原理和应用[M].国防工业出版社,2003.

[11]ANDRONOV V,BAKHRAKH SM,MESHKOV E E,MOKHOV V N,NIKIFOROV V V,PEVNITSKII A V,TOLSHMYAKOV A I.Turbulent mixing at contact surface accelerated by shock waves[J].Sov.Phys.JETP,1976,44:424.

[12]YOUNGS D L.Numerical simulation of mixing by Rayleigh-Taylor and Richtmyer-Meshkov instabilities[J].Laser and Particle Beams,1994,12(4):725-750.

[13]POGGIF,THOREMBEY M H,RODRIGUEZ G.Velocity measurements in turbulent gaseous mixtures induced by Richtmyer-Meshkov instability[J].Phys.Fluids,1998,10(11):2698-2700.

[14]M UGLERC,GAUTHIER S.Two-dimensional Navier-Stokes simulations of gaseous mixtures induced by Richtmyer-Meshkov instability[J].Phys.Fluids,2000,12(7):1783-1798.