平衡态近似及其与稳定态近似的关系

刘国杰 黑恩成

(华东理工大学化学系 上海 200237)

平衡态近似及其与稳定态近似的关系

刘国杰 黑恩成

(华东理工大学化学系 上海 200237)

对平衡态近似作了简述,表明它与稳定态近似是两种不同的处理方法。当平衡常数K≪1时,平衡态近似是稳定态近似的一个特例。两种近似可以归纳成一个统一的反应速率方程,它具有更广的适用范围。

在反应机理的拟定中,平衡态近似和稳定态近似是两种最常用的方法。对于它们间的关系,物理化学教材和专著中常有不同的看法。有些教材[1-2]认为,它们是两种不同的处理方法;有些专著[3-4]则认为平衡态近似是稳定态近似的一个特例,前者包容于后者之中。显然,明确两者之间的关系是非常必要的,本文试图通过对平衡态近似的简述,来阐明它们间的关系。

1 平衡态近似

平衡态近似亦称预平衡近似或速控步近似。假如有一个反应

其中B为中间物。则平衡态近似就是假定反应过程中反应物 A与中间物 B之间能始终近似地保持化学平衡,即:

严格说来,此时 cA和 cB应分别为反应物和中间物的平衡浓度 cAeq和 cBeq。于是,由式 (1)可得:

式中 K=k1/k-1。K为平衡常数,要满足这个平衡条件,机理中的第 2步中间物 B变为产物 P的速率必须很慢,亦即这一步应是速率控制步骤,总反应速率就取决于这一步。

这也意味着中间物B返回反应物A的速率远大于它转变成产物 P的速率,否则,A与 B间的平衡便难以保持。这就是说

式(4)便是平衡态近似的适用条件。

将式 (2)代入式 (3),得总反应速率方程为:

由于机理的第 1步是处在平衡之中,故由物料恒算,不难得到未反应的A的总浓度为:

式中 cA0为反应物A的初始浓度。

若将式 (2)代入式 (6),则可得:

现将式 (7)代入式 (5),便得总反应速率方程为:

式(8)即为平衡态近似得到的结果。由于总反应速率系数为:

故平衡态近似的特征是:k/k2是平衡常数 K的函数。当 K≪1时,k/k2趋近于 0;当 K≫1时, k/k2趋近于 1,图 1是 k/k2对 K作图,可见,随着平衡常数 K增大,k/k2从 0逐渐增大,最终趋近于极限值 1。

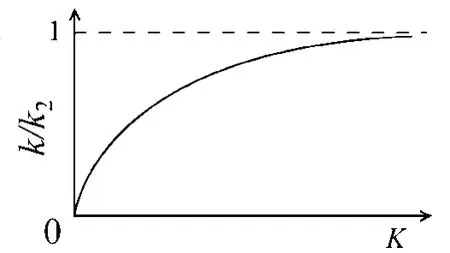
图1 k/k2与 K的关系

显而易见,这个近似不同于稳定态近似,它不要求中间物浓度处于稳定状态,也不要求中间物浓度很小或很活泼,而是令反应物与中间物近似地处于平衡状态,故原则上是一种独立于稳定态近似的处理方法。

2 平衡态近似与稳定态近似间的关系

然而,值得关注的是,绝大多数专著和物理化学教材都将注意力集中在 K≪1的情况。此时因 cBeq≪ cAeq,中间物B的平衡浓度极小,是一个难以用实验测定的物质,或许正是由于这个原因,它为反应机理中的中间物结构留下了一个可供“想象”的空间。

于是,由式 (6)可得 cA≈cAeq,将它代入式 (5)或式 (8),可得到:

由于在此情况下,k1≪k-1,若将它与式 (4)相结合,则这两个不等式可隐含于下式之中:

式 (11)正是稳定态近似的适用条件 (若反应时间大于诱导期)[3],故在此情况下,式 (10)也可通过稳定态近似得到。

对于上述反应机理,若用稳定态近似,应为:

这便是稳定态近似得到的总反应速率方程。不难发现,它与平衡态近似得到的式 (8)在形式上很相似。

若将平衡态近似的适用条件式 (4)代入式 (14),便可得到式 (10)。因此,式 (10)也可视为是在中间物B的浓度处于稳定态的前提下,再代入平衡态近似的适用条件(式 (4))所得的结果。显然,此时的平衡态近似是包容在稳定态近似之中的,前者只是后者的一个特例[3-4]。

应该指出,目前国内的物理化学教材在叙述平衡态近似时,都没有考虑到 cA和 cB与和间的区别,而是用 cA取代,cB取代。于是,式 (2)便变为:

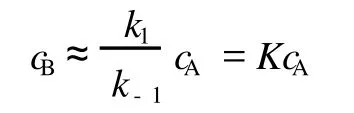
由速控步便可得到总反应速率方程为:

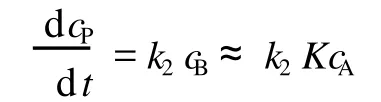
此式即为式(10)。这就默认了推导是在 K≪1的条件下进行,因为只有在满足这个条件时,由式 (7)才能得到 cA≈ceqA。故这时的平衡态近似是稳定态近似的一个特例。但当 K不是≪1时,它便不再包容于稳定态近似之中,而是一种独立于稳定态近似的处理方法。

3 一个改进的反应速率方程

如上所述,平衡态近似得到的反应速率方程如式 (8)所示,其适用条件为 k-1≫k2,故在式(8)等号右边的分母中加上 k2是无妨的。有趣的是,稳定态近似导得的反应速率方程如式(14)所示,其适用条件为 k-1+k2≫k1,因此,在式 (14)等号右边的分母中加上 k1亦无妨。这样,两种近似便得到了如下相同的反应速率方程:

这就是说,它不仅适用于平衡态近似,而且也适用于稳定态近似。例如,当 k-1≫k2时,相比于k-1,分母中的 k2可以忽略不计,式 (15)便变成式 (8);而当 k-1+k2≫k1时,相比于 k-1+k2,分母中的 k1可以忽略不计,式 (15)便变成式 (14)。故式 (15)是一个能兼顾两种近似的统一的反应速率方程,它有着更广的适用范围。

文献[5]列出了 k1,k-1和 k2不同相对大小的 12种情况,讨论了两种近似对它们的适用状况。表 1则进一步表示了式(8)、式 (14)和式 (15)对这 12种情况的适用性。

由表 1可见,式(15)有更广泛的适用性。虽然从理论上说,它依然不适用于表 1中的条件⑧、⑩和 ○11 ,但因上述反应机理中的 k1、k-1和 k2是可以严格求解的[4],故对于条件⑩,若令k1:k2:k-1=1:1:10-2,则式 (15)仍可得到较满意的结果[6]。

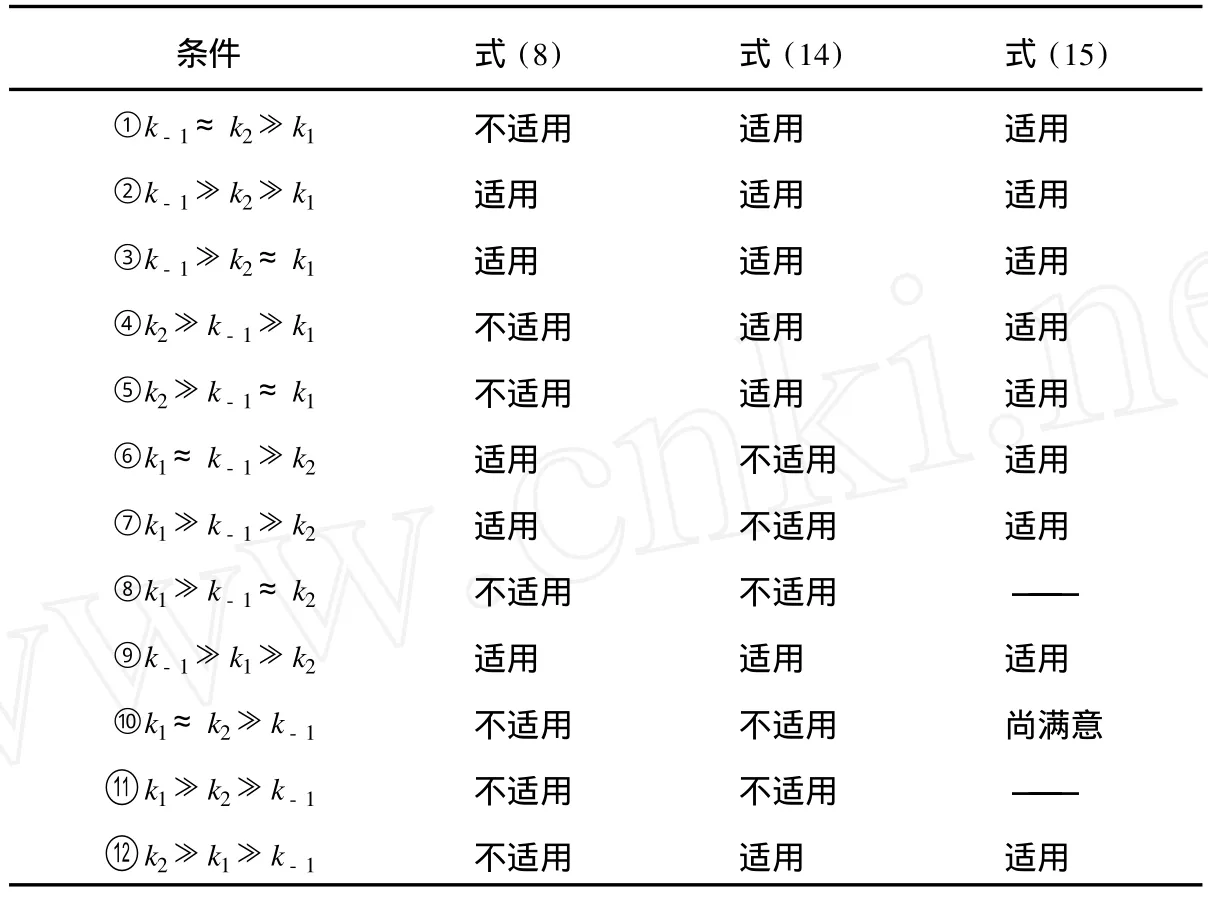
表1 式(8)、式(14)和式(15)对 12种情况的适用性

4 结论

综上所述,本文得到如下几点结论:

1)不同于稳定态近似,平衡态近似不要求中间物浓度处于稳定状态,也不要求中间物浓度极小或很活泼,而是令反应物与中间物近似地处于平衡状态。两者的适用条件也不相同,除了反应时间大于诱导期外,平衡态近似的适用条件为 k-1≫k2,而稳定态近似的适用条件为k-1+k2≫k1,故原则上它们是两种独立的处理方法。

2)当平衡常数 K≪1,即 k-1≫k1时,因 k-1≫k2和 k-1≫k1可联合表示为 k-1+k2≫k1,这时的平衡态近似方可认为是稳定态近似的一个特例。值得注意的是,几乎所有物理化学教科书实际上都是在默认这个条件的前提下叙述和讨论平衡态近似的,因此,平衡态近似也就包容在稳定态近似之中。

3)由平衡态近似和稳定态近似可以得到一个统一的反应速率方程,它能兼顾这两种近似,使反应速率方程具有更广的适用性。

[1] 胡英,吕瑞东,刘国杰,等.物理化学.第 5版.北京:高等教育出版社,2007

[2] 王正烈,王亚平.物理化学.第4版.北京:高等教育出版社,2001

[3] 赵学庄.化学反应动力学原理(上册).北京:高等教育出版社,1984

[4] Moore J W,Pearson R G.Kinetics andMechanis m.3rd ed.New York:JohnW iley&Sons,1981

[5] 香雅正.化学通报,1988(4):57

[6] Espenson J H.Chemical Kinetics and ReactionMechanis m.2nd ed.New York:McGraw-Hill,1995