POLYMATH软件在化工课程中的应用

李学慧 吴正舜伍强贤 陈义峰 刘雪莲

(华中师范大学化学学院 湖北武汉 430079)

计算机与化学

POLYMATH软件在化工课程中的应用

李学慧 吴正舜＊伍强贤 陈义峰 刘雪莲

(华中师范大学化学学院 湖北武汉 430079)

以化学工程中的非线性方程、复杂函数的积分、离散数据点的处理、实验数据点的回归分析以及线性微分方程组求解为例,讨论 POLY MATH软件在化学与化工课程中的应用。结果表明:利用 POLY MATH求解计算问题稳定性好、方便快捷;能把学生从复杂的编程与调试中解脱出来,并能提高学生的学习效率以及分析问题和解决问题的能力。

化学工程专业教学计划规定的许多基础课程、专业课程均涉及复杂的计算技术,因此,在学完高等数学、工程数学、化工数学以及算法语言、物理化学、化工原理等先修课程后,掌握和使用化工计算软件对学习化工热力学、反应工程、分离工程、化工系统工程、化工工艺学等后续课程都将起到积极作用,掌握化工计算软件对学生理解这些课程的内容、提高教学效率具有重要意义。

化学工程通常以实际工程问题为研究背景,由于化学反应速率与温度及浓度为非线性关系,导致求解时经常涉及非线性方程、线性微分方程 (组)和偏微分方程 (组)、复杂函数的积分、离散数据点的处理、实验数据点的回归分析、插值与曲线拟合、以及图解等工程计算[1]。尽管可以用计算机语言编写程序解决上述问题,但在用计算机语言编程时,既需要对有关算法有深刻的了解,还需要熟练掌握所用语言的语法及编程技巧,对多数本科生而言,同时具备这两方面能力有一定的困难。此外,繁杂程序的编写,不仅耗废人力与物力,而且还影响工作进程和效率。

POLY MATH软件是美国康涅狄格大学MichaelB.Cutlip等人为化工类专业大学生及研究生开发的一种用于工程计算和数值分析领域的软件包,它拥有专门的命令集和查用函数集,可以完成各种计算和数据处理,形式简便,易于掌握[2]。虽然 POLY MATH软件也需要学习,但由于用 POLY MATH编程类似纸上排列出公式与求解问题,所以编程效率高,易学易用,而不像学习其他高级语言那样难以掌握。实践证明,大学生可在几十分钟的时间内学会 POLY MATH的基本知识,经过短短几个小时的使用就能掌握它,从而能够进行高效率和富有创造力的计算。应用该软件处理化工计算具有处理物性数据速度快,循环重复计算方便,能灵活选择和修改参数的特点。

本文以求解化学工程中常见的非线性方程、复杂函数的积分、离散数据点的处理、实验数据点的回归分析以及线性微分方程组为例,介绍 POLY MATH软件的应用,以期在化学工程与工艺以及相关专业中推广应用,把学生从繁琐的编程求解中解脱出来,让学生在求解过程中加深对过程所涉及的基本原理的理解,提高学习效率。

1 求解非线性方程

在化学工程中有关非线性方程的求解非常多,如分离工程中的泡点或露点温度的计算,化工热力学中真实气体状态参数的求取等,这些方程需要编程迭代求解。使用 POLY MATH软件可将编程迭代求解作为一个函数库放在软件包中,只须按要求输入相关的非线性方程调用即可。如:

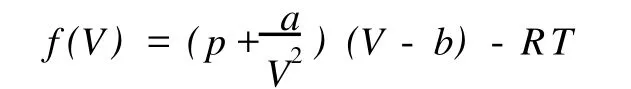
求 p=56.728×105Pa,T=450K时所对应的体积,已知该物质的临界参数为:Tc=405.5K, pc=112.7469×105Pa,于是可用 POLY MATH方便地求解(图 1,图 2)。

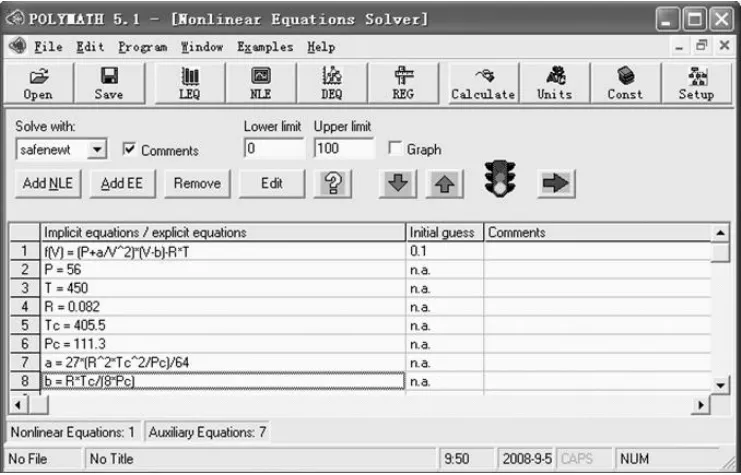
图1 POLYMATH在求解非线性方程时的输入界面

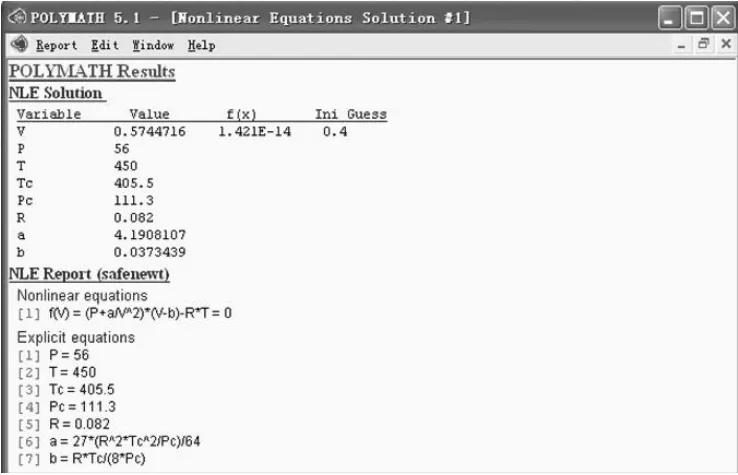
图2 POLYMATH在求解非线性方程时的结果输出界面

求解得对应的体积为V=0.5745L。

2 求解复杂函数的积分

在化学反应工程中,反应器的体积和催化剂用量的求取经常涉及到复杂函数的积分,如:

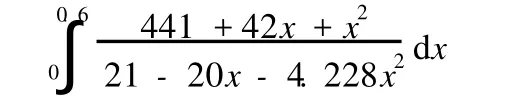
可通过 POLY MATH软件简单地完成(图 3,图 4)。

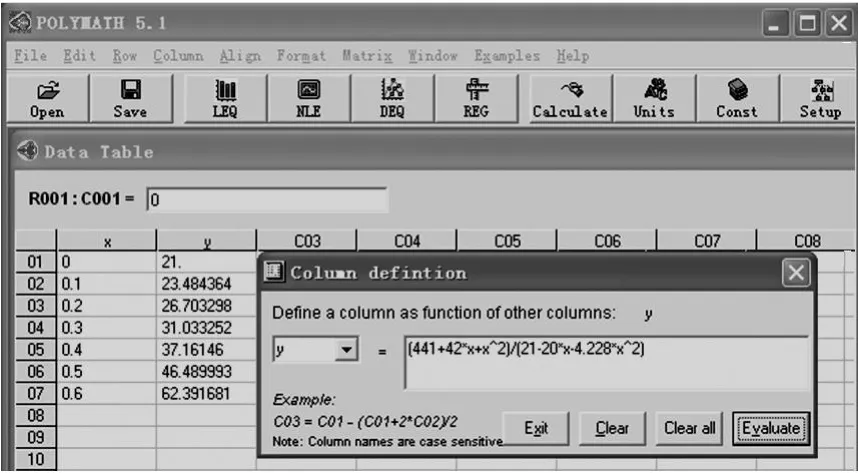
图3 POLYMATH求解复杂函数积分时的处理界面

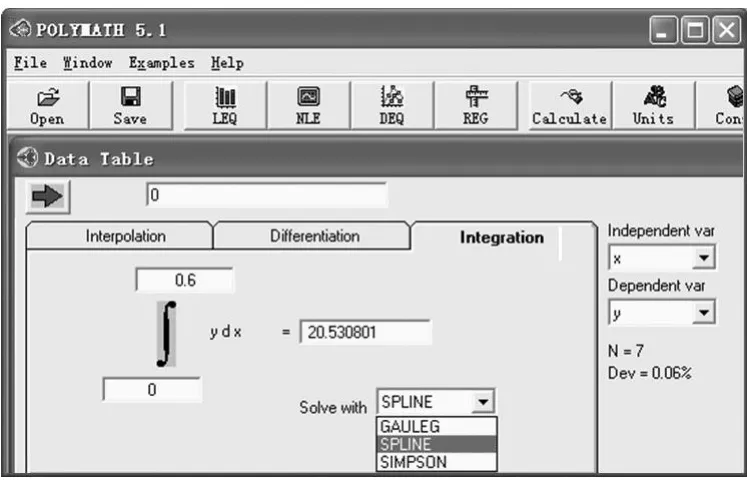
图4 POLYMATH求解复杂函数积分时的结果输出界面

POLY MATH软件可根据积分的上下限先将连续函数离散化,并求出对应的函数值,再通过对离散点的积分并选择合适的计算方法得出函数的积分值。

3 用于离散点的数学处理

在化学工程以及实验中常有关于离散点的数学处理,虽然可用数学方法处理,但有时精度达不到,尤其对于非等间隔的离散点的处理,既要满足精度,又要便捷,这对于学生是有难度的。例如用阶跃法测停留分布中的出口示踪物的质量浓度 (表 1)。

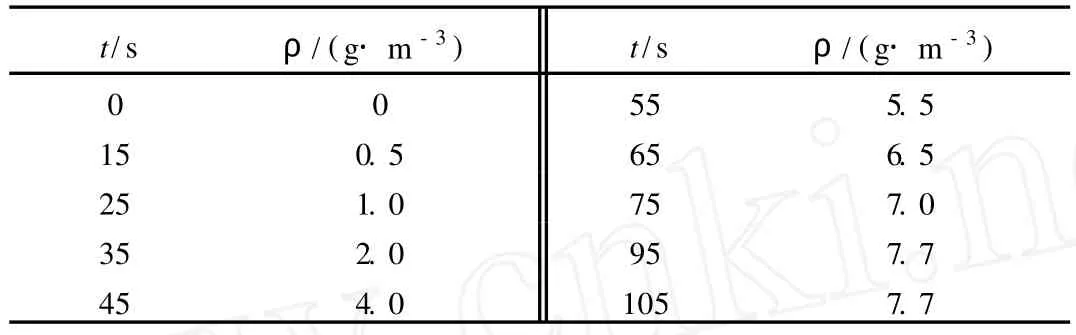
表1 不同时间条件下反应器出口检测到的示踪剂质量浓度

由化学反应工程原理知:

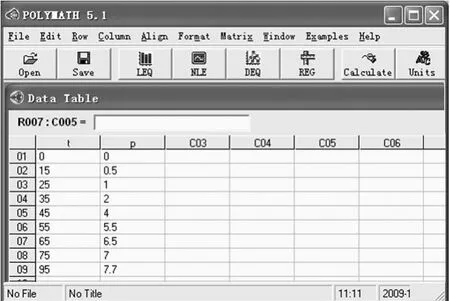
图5 POLYMATH求解离散点积分的处理界面

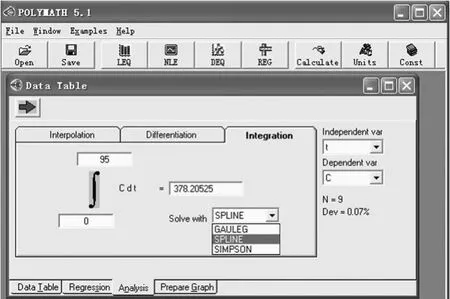
图6 POLYMATH求解离散点积分的结果输出界面

4 用于数据回归分析

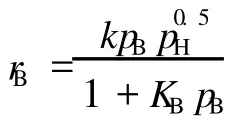
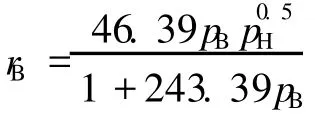
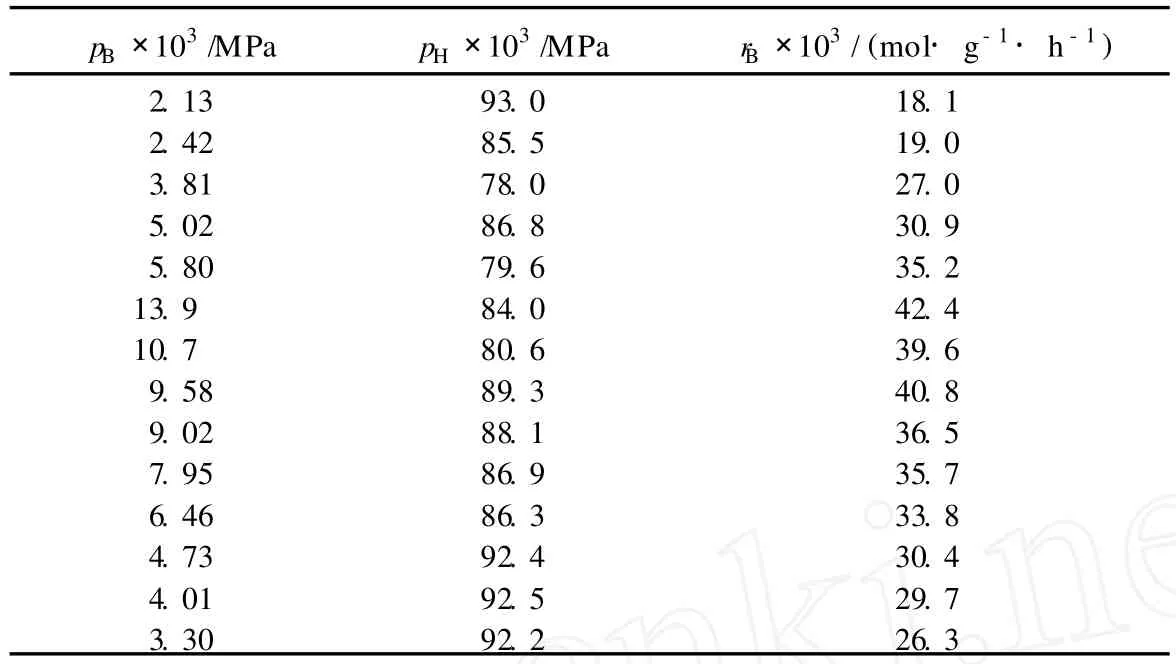
表2 不同条件下所测得的反应速率数据

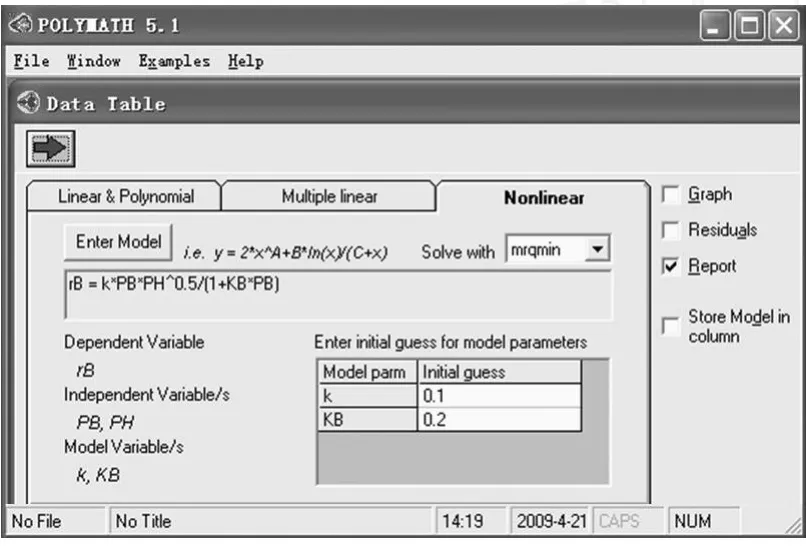
图7 POLYMATH在数据的回归分析中输入求解线性或非线型模型时的界面

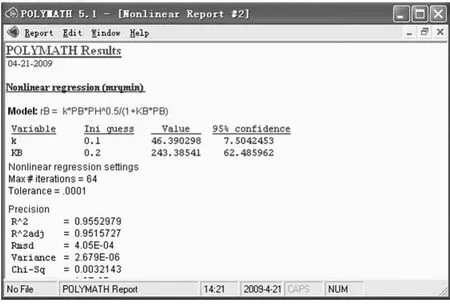
图8 POLYMATH在数据的回归分析中求解的模型参数输出界面

5 求解微分方程组

在化学反应工程中通过对控制体的物料衡算及热量衡算可得到下列微分方程组:

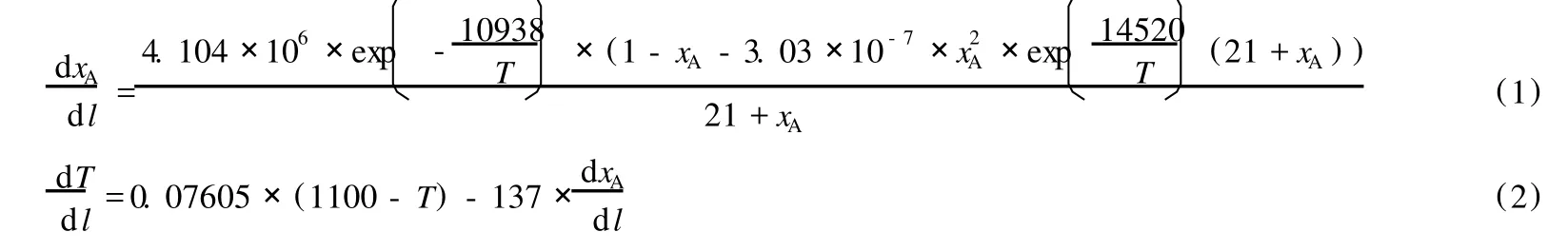
该微分方程组的边界条件为:当反应物料刚进入反应器长度为 l的反应器时,l=0,反应物料的温度 T=898K,反应物料转化率 xA=0。

通过 POLY MATH软件可以方便地完成微分方程或微分方程组的求解,求解过程见图 9。从图 9可以看出:编程语言的数学表达形式很接近传统的数学书写风格,不需要使用复杂的程序设计以及编程技巧,从而把人们从复杂的编程与调试中解脱出来,用更多的时间去理解模拟过程所涉及的基本原理,微分方程组的求解的结果见图 10。

此外,用 POLY MATH软件求解的结果也可用表格直观显示转化率 xA及床层温度 T沿轴向分布相关结果(图 11)。

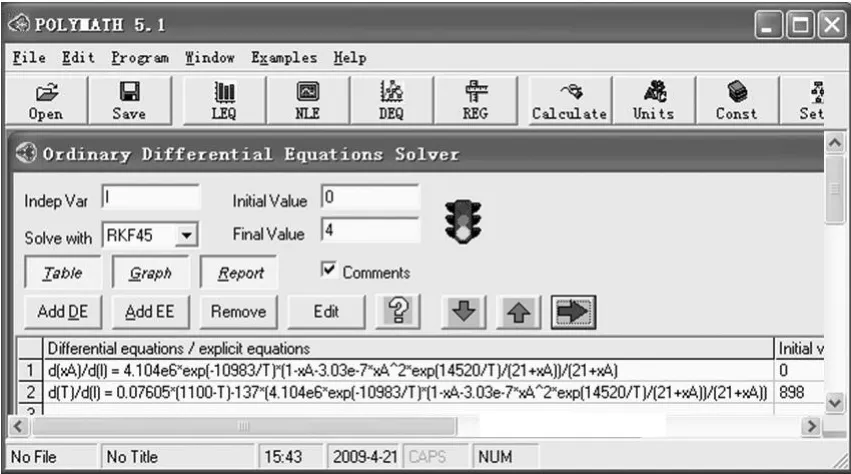
图9 POLYMATH在求解微分方程组时的输入界面

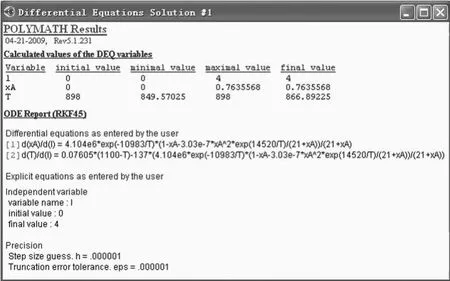
图10 POLYMATH在求解微分方程组的结果输出界面

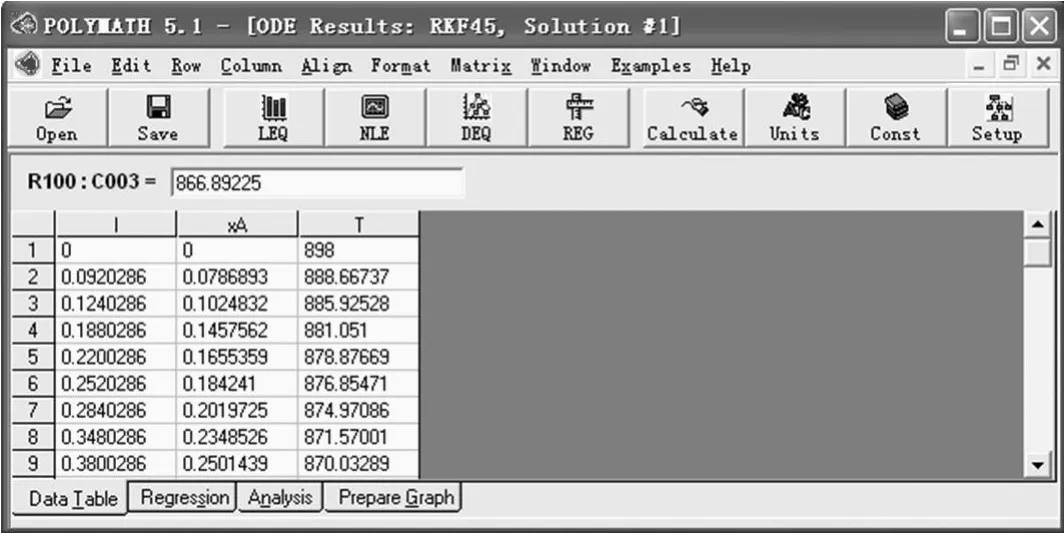
图11 POLYMATH在求解微分方程组时的数据结果输出界面

6 结论

通过上述应用 POLY MATH软件包求解化学工程中的非线性方程、复杂函数的积分、离散数据点的处理、实验数据点的回归分析以及线性微分方程组求解数学软件示例,可知利用POLY MATH能够高效、便捷地解决化学反应工程的数学问题,尤其是在解非线性方程(组)、微分方程和偏微分方程(组)、插值与曲线拟合、数值积分、以及图像处理等工程问题方面,POLYMATH比其他软件更优越,除了具有易使用和功能强大的工具盒外,更重要的是其编程语言的表达形式很接近传统的数学书写风格,在课堂上能将复杂的工业反应过程的计算问题实时生成可改变操作条件的组成 (转化率)、温度或反应速率的分布图,得到令人满意的教学效果。总之,POLY MATH能把人们从复杂的编程与调试中解脱出来,使人们可以用更多的时间去关注化学工程本身所涉及的基本原理,是解决化学工程相关计算的好工具。

[1] 李绍芬.化学反应工程.第 2版.北京:化学工业出版社,2006

[2] Cutlip M B,Shacham M.Problem Solving in Chemical and Biochemical Engineering with Polymath,Excel,and Matlab.New York:Pearson Education,2007

＊ 通讯联系人,E-mail:wuzs@mail.ccnu.edu.cn