基于蕴涵法的求解多变量逻辑函数本原蕴涵项的程序流程

王波 徐州师范大学计算机科学与技术学院 221116

基于蕴涵法的求解多变量逻辑函数本原蕴涵项的程序流程

王波 徐州师范大学计算机科学与技术学院 221116

基于逻辑函数蕴涵化简法的基本理论，构造比较合并数组，设计求解多变量逻辑函数本原蕴涵项的结构化程序流程，使逻辑函数的化简工作在降低了复杂度的同时提高了可靠性。

蕴涵化简法；本原蕴涵项；逻辑相邻项；结构化流程

引言

通过化简实现逻辑函数的最小化是数字逻辑系统设计过程中非常重要的一个步骤，但诸如公式法、卡诺图法等常用的化简方法仅适用于简单的逻辑函数，对于复杂的多变量（5变量以上）逻辑函数的化简则可使用蕴涵化简法。

蕴涵法又叫制表法，是由奎恩（Quine）提出，并经由麦克拉斯基（McCluskey）改进和完善的一种逻辑函数系统化简法，故又称为Q－M化简法。虽然与卡诺图法一样也是以公式为基本理论依据，但蕴涵法又有着化简步骤规律性强的优点，应用于多变量逻辑函数的化简，虽然工作量大，但操作可以按部就班地进行，适合于计算机处理[1]。

上述特点，在蕴涵法化简逻辑函数的第一个步骤即求本原蕴涵项的过程中表现得尤为突出。所谓本原蕴涵项就是不含多余变量的乘积项，即其已不能再通过同其它乘积项合并而减少变量了[2]。本文以5变量逻辑函数为例，应用蕴涵法进行计算机辅助设计，给出求解多变量逻辑函数本原蕴涵项的结构化程序流程。

1.程序流程

1.1 初始化

初始化操作除了定义程序运行所需的多个相关变量外，最主要的工作就是定义如下两个数组。

1.1.1 二维数组m[3][212]

m数组的每个数组元素为一个字节，同一列的三个数组元素构成一个数据单元，数组元素的列号即为数据单元的序号，如图1所示，数据单元是存储逻辑函数标准与或式中包含的最小项或操作过程中产生的一般乘积项的基本单位。

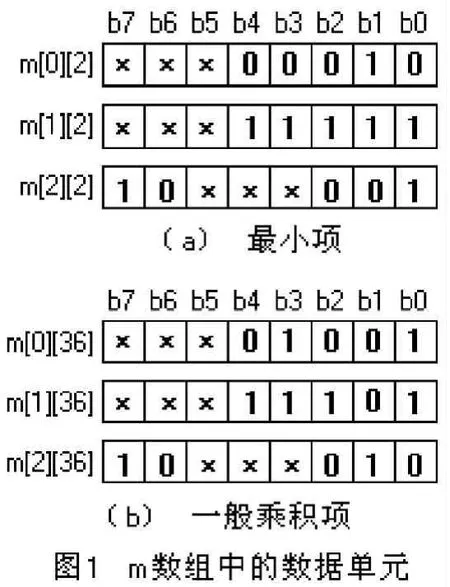
数据单元中标记“×”的位没有定义（用“0”填充），其余位根据不同的存储对象有着不同的定义和使用方法。

（1）存储最小项

按照使最小项、数据单元的序号对应相等的方法，将逻辑函数包含的最小项mi存储于m数组的第i（=0～31）个数据单元并由输入程序作相应设置。

1）m[2][i].7位为“1”，表示逻辑函数包含最小项mi，此时，数据单元的其它各位定义如下。

①m[2][i].6位为“0”，表示mi尚未被消去任何变量，一旦mi参与化简，此位将被置“1”；

②m[0][i].4～m[0][i].0位组存储mi的序号i对应的5位二进制数，其中“1”对应mi中的原变量，而“0”对应反变量；

③m[1][i].4～m[1][i].0位组存储5个连续的二进制“1”表示mi包含所有逻辑变量；

④m[2][i].2～m[2][i].0位组用于存储3位二进制值，表示位组m[0][i].4～m[0][i]. 0中“1”的个数，即mi中原变量的个数。

图1（a）为一个特例，描述最小项m2尚未参与化简合并时的存储状态。

2）m[2][i].7位为“0”表示逻辑函数不包含最小项mi，此数据单元的其它位皆不被定义使用。

（2）存储一般乘积项

在求解本原蕴涵项过程中，一般会产生被消去若干个变量的一般乘积项，它们将被依次存储于m数组中序号大于或等于32的数据单元中,除以下两点外，各数据位取“0”、“1”状态的含义与存储最小项时基本相同。

1）一个一般乘积项在m数组中的具体存储位置由被处理的逻辑函数的结构决定；

2）m[1][i].4～m[1][i].0位组中的某位为“0”，表明其对应的变量已被从乘积项中消去，其在m[0][i].4～m[0][i].0位组中对应位的状态也失去意义。

图1（b）为另一个特例，描述了一个一般乘积项的存储状态，此一般乘积项由逻辑函数F（在后文的实现实例部分中详细说明）包含的两个最小项m9、m11合并得到，其所在数据单元的序号为36，尚需进一步化简。

（3）m数组中数据单元数目的定义问题

对于m数组，实际所需的数据单元的数目由被处理的逻辑函数决定，随逻辑函数包含的最小项数目及最小项分布情况不同而变化。在此，对5变量逻辑函数，设定数据单元的个数为212，即m数组的列号范围为0～211,这是一个存储单元数目极端大的选择，对应逻辑函数的标准与或式中共包含31个最小项的情况。

1.1.2 二维比较合并数组comp[6][10]

为了比较、合并逻辑相邻的最小项，根据蕴涵法理论定义6行10列的二维字节数组comp，并依据表1（最小项比较合并表）的结构和内容将comp数组初始化，comp数组具有如下特征。

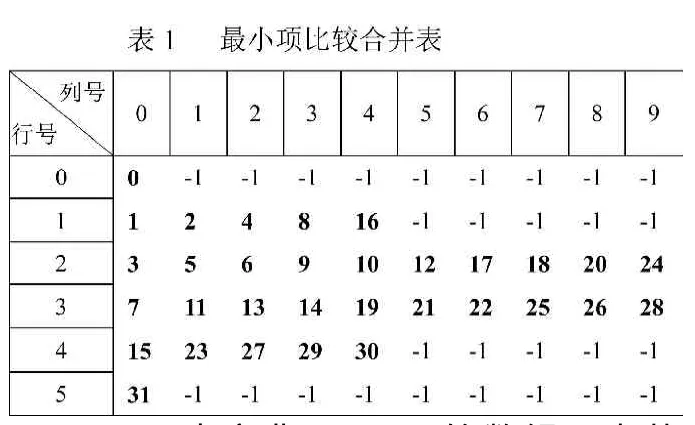
（1）内容非“-1”的数组元素共32个，分别对应被处理逻辑函数可能包含的序号为0～31的32个最小项，而内容为“-1”的数组元素不对应最小项。每行的第一个内容为“-1”的数组元素用于控制某一轮寻找、比较与合并最小项的循环过程的结束。

（2）同一行数组元素对应的最小项拥有相同个数的原变量，并且原变量的个数等于行号。

（3）某行一个数组元素对应的最小项与相邻上一行另一个数组元素对应的最小项相比较，原变量个数多1，如果这种关系是由于逻辑函数的同一个变量在两个最小项中分别取原、反变量状态引起的，则相应的两个最小项即为一对逻辑相邻项。

1.2 逻辑函数输入

输入程序依据前述要求设置m数组的相关数组元素。特别地，对于逻辑函数包含所有最小项（逻辑函数值恒为1）和逻辑函数不包含任何最小项（逻辑函数值恒为0）两种情况要在输入流程中直接进行处理说明，而不必进入后续的求解本原蕴涵项流程。

1.3 求解本原蕴涵项流程

求解本原蕴涵项操作的程序流程结构为一个整体，为描述方便，将其分为主体和子模块两个部分。

1.3.1 主体部分

图2以N-S图的形式给出主体部分的结构化流程。

这一部分的核心流程是一个严格遵循蕴涵法基本步骤设计的，分别以i1、j1和k1为外、中和内层循环控制变量的三重嵌套循环结构。借助于comp数组为主要的控制依托，通过此循环结构正常运行，可实现主体部分的基本功能，即进行逻辑相邻最小项的寻找、比较与合并操作，得到因消去一个变量而拥有4个变量的所有一般乘积项，并依次存储于m数组中相应位置的数据单元中。

当得到的4变量一般乘积项的个数大于或等于2时，求解本原蕴涵项的操作过程就需要继续进行，流程进而由此部分结束处的二重嵌套选择结构的最左端分支进入子模块部分，否则，本原蕴涵项已经求出，整个流程结束。

1.3.2 子模块部分

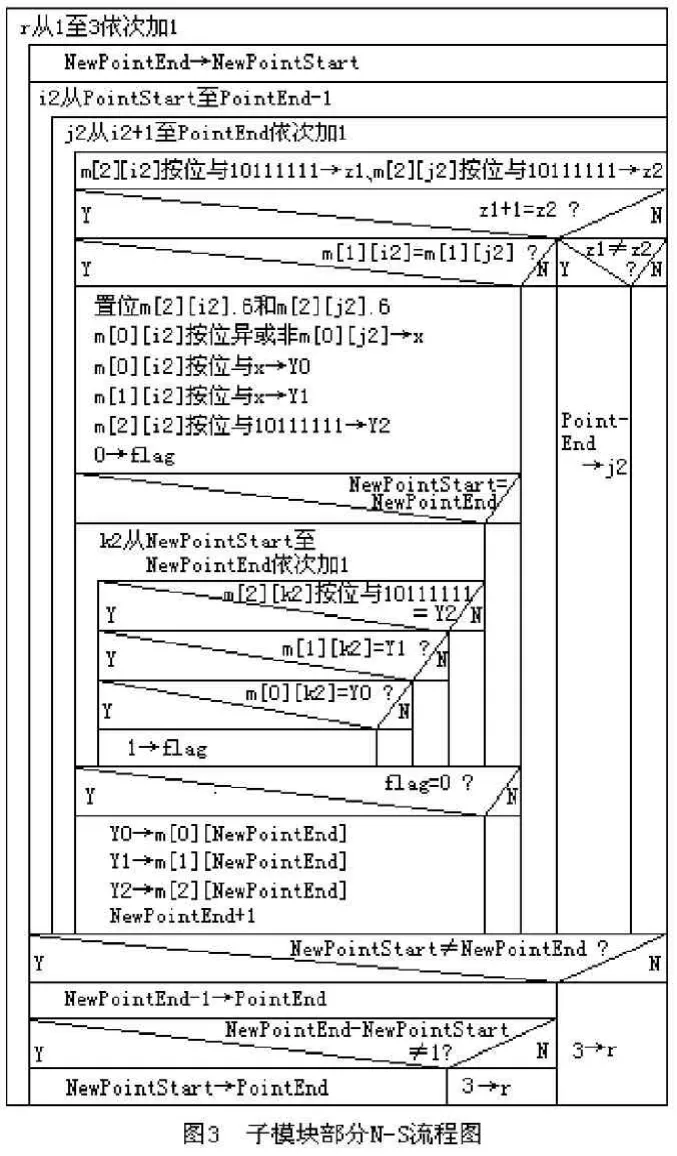
图3以N-S图的形式给出子模块部分的结构化流程。

子模块部分实现的功能是：针对主体部分求得的两个或两个以上的4变量一般乘积项，继续进行逻辑相邻的一般乘积项的寻找、比较与合并操作。

这一部分程序流程整体上为一个四重嵌套的循环结构。以r为循环控制变量的外层循环最多可能执行3次，先后求得可能存在的由3、2或1个逻辑变量组成的一般乘积项；i2、j2控制中间两层循环，实施求解这些一般乘积项的具体操作；而k2控制的最内层循环则用于防止同一个一般乘积项在m数组中的重复存储。

1.4 本原蕴涵项的输出

上述相关流程执行完毕后，化简得到的所有本原蕴涵项都被存储在m数组中，假设某个本原蕴涵项所在数据单元的序号为i，则有：

（1）i的范围为0～PointEnd；

（2）m[2][i].7～m[2][i].6位组的内容为“10”（此为本原蕴涵项的标志）；

（3）m[1][i].4～m[1][i].0位组中内容为“1”的位对应的变量被保留在本原蕴涵项中；

（4）本原蕴涵项中一个被保留变量的原、反状态由m[0][i].4～m[0][i].0位组中此变量对应位的取值确定，“1”对应原变量，“0”对应反变量。

根据上述特征，可设计相应的程序流程对所有本原蕴涵项进行依次输出。

2.实现实例

用蕴涵法化简逻辑函数F（A、B、C、D、E）=∑m（0,2,4,6,9,11,13,15,17, 21,25,27,29,31），求全部本原蕴涵项[3]。用C语言实现上述流程，程序运行的结果是在m数组中得到3个存储着本原蕴涵项的数据单元，它们是：

①m[0][51]=00000000、m[1][51]=00011001、m[2][51]=1000000；

②m[0][55]=00010001、m[1][55]=00010011、m[2][55]=1000010；

③m[0][59]=00001001、m[1][59]=00001001、m[2][59]=1000010。

3.结束语

本文介绍的求解多变量逻辑函数本原蕴涵项的方法严格遵循蕴涵法理论，设计的程序流程清晰、准确，符合结构化标准，用C、VB等高级编程工具很容易实现。对于6变量以上的逻辑函数，也仅仅需要对m数组的列数、comp数组的结构和内容及部分循环结构的循环次数进行简单的修改即可。实践表明，通过上述流程对逻辑函数进行处理的结果，与用公式法、卡诺图法等手工方法进行处理的结果完全一致，但在提高可靠性、减小复杂度和降低工作成本等方面优点是明显的。

[1]朱勇，高晓清，曾西洋．数字逻辑第一版．北京：中国铁道出版社．2007；49

[2，3]韩振振，李亚伯．数字电路逻辑设计[M]．第一版．大连：大连理工大学出版社．1987；105－116

10.3969/j.issn.1001-8972.2010.24.014

王波，男，汉族，现任教于徐州师范大学计算机科学与技术学院，主要研究方向：数字系统设计，单片机及嵌入式系统。