商业银行对房地产企业信用评价方法研究

李 楠 刘志杰

1 研究意义

现代商业银行经营管理的核心内容之一就是风险管理。在我国,信用风险度量和管理方面的研究和运用相当滞后,信用风险度量和评级主要是定性方法,方法简单而粗糙,缺乏一致性和有效性。近几年,房地产业成为我国国民经济的支柱产业之一。由于房贷资产质量相对较高,房地产信贷业务中所产生的金融风险较其他种类的信贷业务而言相对较小,商业银行普遍大力发展房地产信贷,加大了金融风险的存在。因此我国商业银行房地产信贷面临着比较大的风险,制定必要的防范措施,是我国商业银行必须完成的任务[1]。

2 房地产企业信用评价指标体系的确立

指标选取如表1所示。

表1 指标体系

3 评价模型的选择及应用

Logistic函数(罗吉斯蒂函数)又称增长函数。Logistic回归在信用评价领域应用已经相对比较成熟,并被认为在诸多统计学方法中精确性和稳健性较高,关键在于Logistic回归可以克服其他统计学模型的很多缺点,在分类中具有较好的特性[2]。

3.1 Logistic回归模型基本原理

本文将是否获得贷款 y与指标变量xi之间通过pi(给定 xi条件下y=1的概率)发生关系。该模型可表示为 f(x)=ln[pi/(1-pi)],建立回归模型方程为:

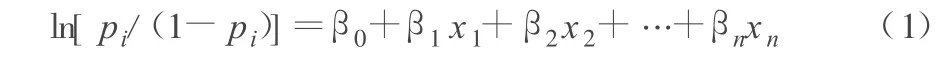
给定一组客户样本{(xi,yi),其中,xi为企业的指标变量;yi为一个二分类的属性变量,yi∈[0,1](yi=0表示第 i个企业违约,yi=1表示第 i个企业不违约),使用 Logistic回归模型可以用来判断一个企业是否违约,公式如下:

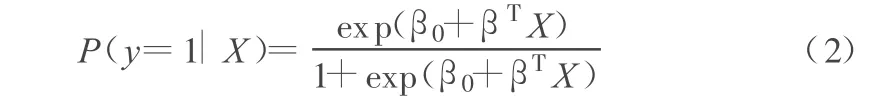
其中,X为m维向量;β为维待求的系数。通过极大似然估计法进行求解:

设从总体中随机抽取n个样本,分别表示为y1,y2,…,yn,设Pi=P(yi=1|X),在给定的 xi条件下,yi=1的概率。同理可得,yi=0的概率可表示为:P(yi)=( 1-Pi)1-yi。

因为各项观测相互独立,其充分必要条件就是其联合概率分布,设为L(θ)等于各边界分布的乘积:

其中,L(θ)为n个观测值的似然函数。对于确定的标本值yi(i=1,2,…,n)来说,它是 β0和 β1(i=1,2,…,n)的函数,即我们的目的是求出参数的估计量,且应使 L(θ)最大,选择使 ln[L(θ)]最大,根据 Logistic函数,可以得到式(4):

分别对 βi(i=0,1,…,m)求偏导数,并令其为0,得到公式:

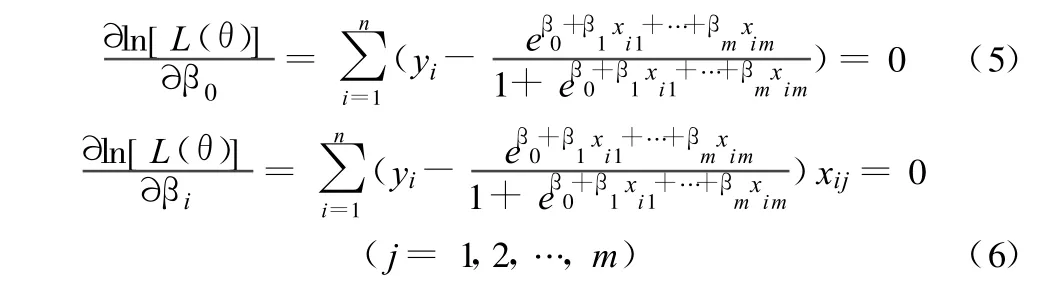
式(5)与式(6)得出的βi为极大似然估计,而相应的条件概率估计值为Pi,这个值是指在给定的 xi的条件下yi=1的概率估计值,其代表了Logistic回归模型的拟合值或预测值[3]。

3.2 指标数据的选择和处理

主要选取上市的房地产公司与本地的房地产企业截至2008年12月的财务及其他指标数据,其中上市的公司股票包括ST股票与*ST股票。对指标进行无量纲化处理,使指标介于[0,1]之间,所谓无量纲化处理就是对评价指标数值的标准化、正规化处理,它是通过一定的数学变化来消除原始数据量纲影响的方法。

3.3 Logistic模型的应用

采用软件SPSS13.0对数据进行处理,经过对变量筛选方法的逐个实验,使用多元逐步回归分析(step wise)方法对 Logistic回归模型进行变量筛选。表2中,R为判定系数,它是回归方程拟合优度的一个度量,估计值的标准差越小,估计值代表的线性就越大,相关点的离散程度就越大。判定系数与调整判定系数越高说明模型的拟合程度越好[4]。从表2可以看出,经过10步拟合样本的判定系数为1,调整后的判定系数也为1,说明该模型有较好的整体拟合性,已经达到了模型建立的要求。

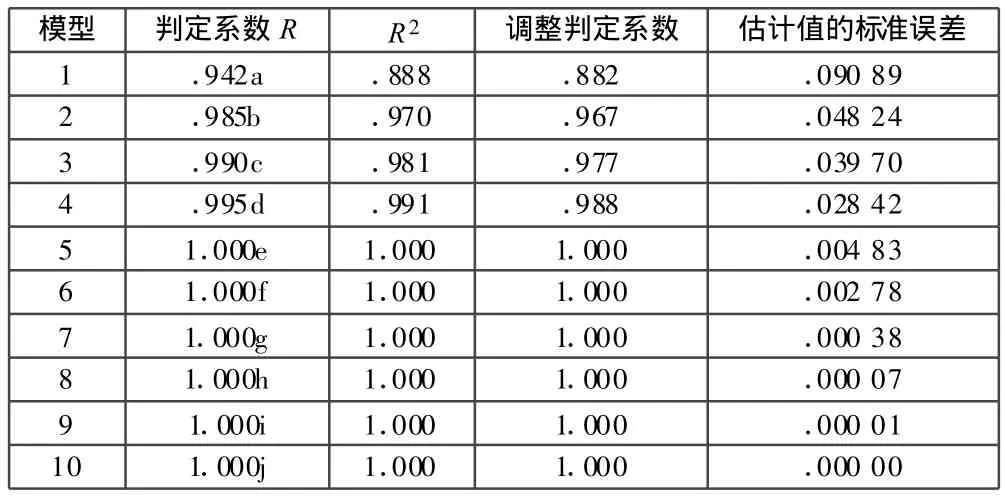
表2 模型总结

表3是指标变量经过9次筛选,最终保留了 x1,x2,x3,x4,x5,x6,x8,x9,x109个变量,变量 x7被剔除。在回归方程中变量被逐一挑选进入回归模型,最后指标 x7被保留,说明指标 x7未进入回归模型,已被剔除。并给出了经过拟合后的模型的指标系数。

通过上面的计算和SPSS分析我们可以得到检验样本的回归模型方程的表达式为:

表3 拟合后的模型指标系数

3.4 应用结果分析

从最终回归模型式(7)的回归系数可以看出,主营业务利润率、净利润率、速动比率、资产负债率、应收账款周转率、土地储备、信用记录、项目市场评估这9项指标会对房地产企业是否违约的概率有较大的影响,这些因素在一定程度上可以反映出企业的还款能力及信用程度。重新选取新的样本带入回归模型检验该模型的稳定性和精确性,模型的准确度均达到了90%以上,可见,模型对样本的稳健性和适应性较好。

4 结语

通过文章的分析,商业银行对房地产企业的信用分析在商业银行信用风险管理中具有重要的作用和意义,所得到的评价结果也就有一定的解释性,但同时由于数据选取的完善性和全面性受到实际情况的制约,这就需要我国建立一个更加规范化的数据库系统,这样才能使信用评价结果更加准确和适用。希望通过本文的研究能使商业银行贷款的信用风险降到最低的同时房地产业能得到最大的收益。

[1]王希迎,丁建臣,陆桂娟.房地产企业融资新解[M].北京:中国经济出版社,2005:94-95.

[2]杨 军.银行信用风险——理论、模型和实证分析[M].北京:中国财政经济出版社,2004:79-82.

[3]许承德,张池平.工科大学数学教程[M].哈尔滨:哈尔滨工业大学出版社,1997:221-229.

[4]吕振通,张凌云.Spss统计分析与应用[M].北京:机械工业出版社,2009:103-209.