数学讲评课五步曲

◆刘小浪

(广东兴宁市龙北中学)

数学讲评课五步曲

◆刘小浪

(广东兴宁市龙北中学)

数学讲评是教学过程的重要一环,缺乏学生主体活动的注入式教法,很难收到应有效果,通过五步教学法可避免费时质低的问题,提高讲评课的实效性。

设计 分析 巩固 提高 跟踪

数学测验、讲评是教学过程的重要一环。目前,数学考试后的讲评课大多被上成教师一讲到底的错题订正课,这种缺乏学生主体活动的注入式教法,很难收到应有的效果。怎样才能上好数学讲评课呢?几年来,我摸索并践行了“设计→分析→巩固→提高→跟踪”五步讲评法,取得了较好效果。

一、评前设计,不可忽视

上数学讲评课时,不少老师思想不够重视,忽视讲评课教案的书写,将试卷从头到尾逐条讲解,面面俱到,既浪费学生的时间,又容易使学生产生厌烦心理,收效甚微。因此,做好评前设计,显得尤为重要。评前设计可包含统计表、巩固练习、拓展习题等内容。用如图所示的双向细目表:

可将每题的得分情况一览无余,从而了解答题情况,知道哪些题答得好,哪些题答得差。对答得差的题,在试卷上注明:答对的同学有哪些 (讲评时便于表扬激励);出现的错误有哪几处;产生错误的症结;避免犯错的方法。对错误较多的共性问题,精心设计一份有针对性的练习题或对原题作适当改变,作为评后的矫正练习,对学有余力的学生,将某些题设计成开放性题,供其探索研究,拓展其思维。做好了评前设计,在讲评时就能真正做到评不足、评误解、评进步、评亮点、评出方向,评出信心。

二、错题分析,对症下药

讲评时,不能“头疼医头,脚疼医脚”。否则,学生的收获往往只会解一道题,不能解一类题,未能很好地体现学生的主动性和积极性。新课程标准指出:“学生是学习的主人,教师是学习的组织者、引导者与合作者。”讲评课也要遵循教师为主导,学生为主体的启发式原则。通过评前的统计,从学生出错的题目中寻找发生错误的根源,对症下药,才能从根本上解决问题,做到纠正一题,明白一理,从而举一反三,掌握一类型。

[例 ]下列命题中正确的个数有 ( )个

①一组对边平行,另一组对边相等的四边形是平行四边形;

②一组邻边相等的菱形是正方形;

③每条对角线分别平分每组对角的四边形是菱形;

④两条对角线相等的四边形是矩形。

A.1 B.2 C.3 D.4

这道题是考查学生对平行四边形、正方形、菱形、矩形的判定的掌握程度,学生难以选择。讲评时,第一步:引导学生发表不同见解,多向交流,先判断每个命题的真假,让判断真命题的学生说出理由,对假命题举出反例加以说明。根据前面统计情况由做错的同学先回答,再由做对的同学加以纠正,并对这一题做对的同学予以表扬。通过讨论达成共识:这道题应选A。因为:①一组对边平行,另一组对边相等的四边形可以为等腰梯形;②一组邻边相等的菱形可能为一般菱形;④两条对角线相等的四边形可以为等腰梯形。

第二步:要求学生把上述假命题订正成真命题,可以得到:

①一组对边平行(相等),另一组对边也平行 (相等)的四边形是平行四边形;

②有一组邻边相等的矩形是正方形;

④两条对角线相等的平行四边形是矩形。

第三步:分组讨论,怎样的四边形是平行四边形、矩形、菱形、正方形。

第四步:制作知识网络图。

这样,学生不仅透彻理解了这道题,而且完善了对平行四边形、矩形、菱形、正方形的认识。

三、强化练习,巩固知识

对于学生错漏较多的共性问题,分析理解后,教师可以及时进行强化练习,作为评讲后的矫正补偿学习,让易错易混淆的问题多次在练习中出现,达到巩固的目的。如在讲完刚才那一题后,可补充如下练习:

1.给出下列命题,其中错误命题的个数有( )

①四条边相等的四边形是正方形

②两组邻边分别相等的四边形是平行四边形

③有一个角是直角的平行四边形是矩形

④矩形、线段都是轴对称图形

A.1个 B.2个 C.3个 D.4个

2.有一个角是直角的_____叫做矩形,对角线_____的平行四边形是矩形,有三个角是直角的_____是矩形;一组邻边相等的_____是菱形,对角线_____的四边形是菱形;______的菱形是正方形,______的矩形是正方形,对角线_____的四边形是正方形。

这样,通过讲、练,学生对平行四边形、矩形、菱形、正方形有了进一步认识,再次碰到类似问题,就能迎刃而解了。

四、因材施教,全面提高

新课标“着眼于全体学生的全面发展”的目标理念。因此,对测试中较难的题目,讲评时要结合学生实际,面向全体,针对中层,顾及两端,可以就同一道题对不同程度的学生提出不同的要求。

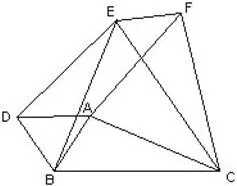
[例 ]已知:如图,以△ABC的三边为边在 BC的同侧分别作三个等边三角形,即△ABD、△BCE、△ACF。求证:四边形ADEF是平行四边形。

部分学生不能找到证平行四边形的条件,讲评时可引导学生有针对性地发现将△ABC分别绕点 B、C旋转 60。可得到△DBE、△FEC,因而可知△ABC≌△DBE≌△FEC,从而有 DE=AC=AF,FE=AB=AD,根据两组对边分别相等的四边形是平行四边形,命题得证。

对学有余力的同学,可提出下列问题:

(1)当△ABC满足什么条件时,四边形 ADEF是矩形?

(2)当△ABC满足什么条件时,四边形 ADEF是菱形?

(3)当△ABC满足什么条件时,四边形 ADEF是正方形?

(4)当△ABC满足什么条件时,以 A、D、E、F为顶点的四边形不存在?

这样,不同的人在数学上得到不同的发展,优等生可以“锦上添花”,中等生可以“更上一层楼”,后进生可力争“赶上队伍”。

五、跟踪辅导,深化效果

在讲评完试题后,要求学生矫正补偿,订在试卷上,收在“错题集”中,作好答题原因分析说明,给出相应的正确解答,教师适时跟踪,对仍未掌握的作个别辅导。复习时,指导学生用好错题集,拿出它,就能明白自己的不足和缺点,从而能及时补救。时间一长,知识基础会越来越牢固,能力会越来越强,重复出现的错误就越来越少,学习信心也就会越来越足,成绩自然也会越来越好。