一类含有2n个非零元的极小谱任意符号模式
王燕玲,邵燕灵
一类含有2n个非零元的极小谱任意符号模式
王燕玲,邵燕灵
(中北大学数学系,山西太原030051)
设A为n阶符号模式矩阵,若对任意给定的一个n次首1实系数多项式f(x),都存在一个实矩阵B∈Q(A),使得B的待征多项式为f(x),则称A为谱任意符号模式.若一个谱任意符号模式的任意真子模式都不是谱任意的,则称这个谱任意符号模式为极小谱任意符号模式.本文给出了一类含有2n个非零元的极小谱任意符号模式.
符号模式矩阵;幂零矩阵;谱任意
0 引言
符号模式矩阵是元素取自于集合{+,-,0}的矩阵.由给定的实矩阵B={bij}的每个元素的符号sign(bij)所组成的矩阵称为B的符号模式矩阵,记为signB.全体n阶符号模式矩阵组成的集合用Qn表示.对任意A∈Qn,所有与A有相同符号模式的n阶实矩阵组成的集合{B|signB=A}称为A的定性矩阵类,记为Q(A).
符号模式矩阵A中的某些非零元被零代替后得出的符号模式称为A的子模式,记作S,也称A为S的母模式.每个符号模式是其本身的母模式和子模式.若S是A的子模式且S≠A.则称S是A的真子模式,A是S的真母模式.
若对任意给定的一个n次首1实系数多项式f(x),都存在一个实矩阵B∈Q(A),使得B的特征多项式为f(x),则称A为谱任意符号模式(SAP).若一个谱任意模式的任意真子模式都不是谱任意的,则称该谱任意模式为极小谱任意模式(MSAP).显然,如果A是谱任意的,那么它一定是惯量任意和蕴含幂零的.对一个n阶符号模式A,若任一矩阵B∈Q(A)是非奇异的,则A是符号非奇异的;若每一个矩阵B∈Q(A)是奇异的,则A是符号奇异的.
谱任意问题最早在文[1]中提出,并据隐函数存在定理给出了一种证明符号模式及其所有母模式是谱任意的方法,第一个n≥2阶谱任意符号模式在文[2]中提出.后来,文[3-9]等文章分别给出了一些惯量任意和谱任意模式.
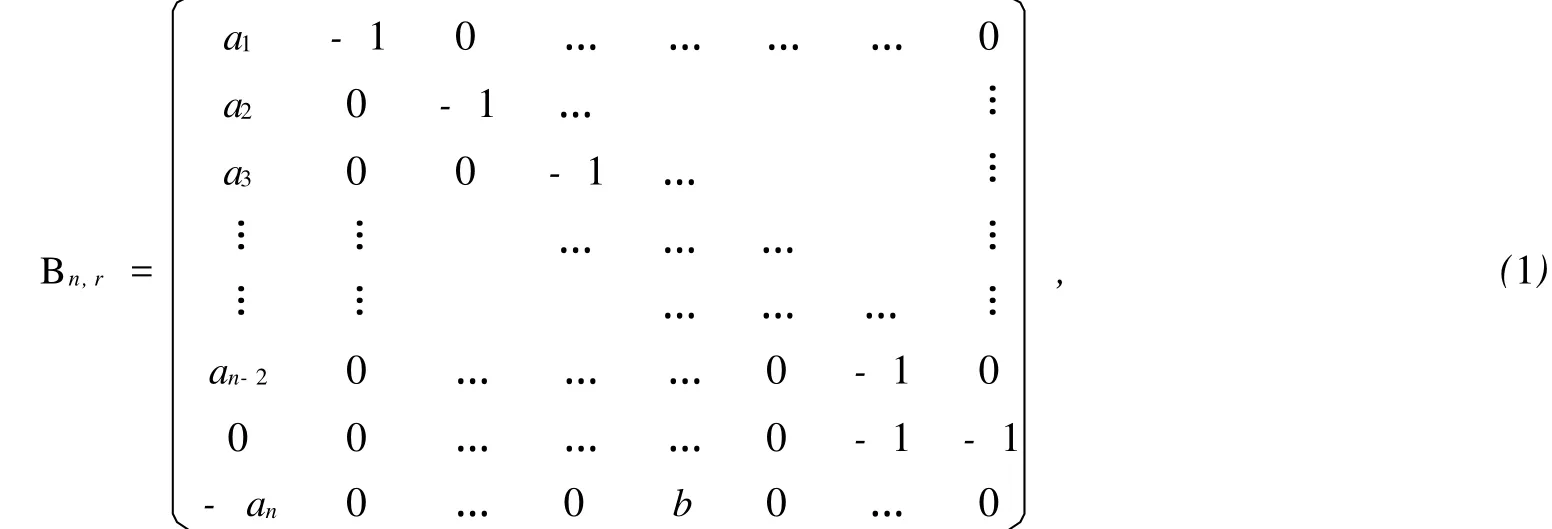
本文研究一类形式如下的n阶符号模式:

其中最后一行的正元在n-r+1列.将证明当n≥3,2≤r 引理1[1]设A∈Qn,假设存在某个幂零矩阵B∈Q(A),且B中至少含有n个零元,记为bi1j1,bi2j2,…, binjn.把B中的这n个非零元用变量x1,…,xn代替后所得的矩阵记为X,设X的特征多项式为pX(x)=xn- α1xn-1+α2xn-2-…+(-1)n-1αn-1x+(-1)nαn.如果当(x1,…,xn)=(ai1j1,…,ainjn)时, 设x1,…,xn是实变量,αi=αi(x1,…,xn)是关于变量x1,…,xn的实函数(其中i=1,2,…,n),且αi对任意xj(j=1,2,…,n)均有连续偏导数.定义函数α1,…,αn对变量x1,…,xn的雅可比矩阵为奇异,则A的任意母模式是谱任意的. 当l≥1,r≥2,且cj>0(j=1,…,l)时,令 其中最后一行的b元在l-r列.若r≥l,则Cl,r中不含b元. 引理2[3]当1≤l≤n且2≤l 任取实矩阵Bn,r∈Q(An,r),设Bn,r有如下形式: 其中b>0,ai>0(i=1,2,…,n-2,n),且b元在n-r+1列. 引理3 设n阶矩阵Bn,r的特征多项式为fBn,r(x)=xn-α1xn-1+α2xn-2-…+(-1)n-1αn-1x+(-1)nαn,令α0=1,则 (1) (2)当a1=1时, 证明(1) 因此(1)成立. 证明(2) 按n-r列展开,可得 由引理2可知,上式是cn-r,r的形式,即det(J)>0.引理得证. 这里给出一个定义,对于一个实系数多项式f(t),令Zf={a>0|f(a)=0},如果Zf非空,则Zf的最小值记作min(Zf). 引理4[3]设f(t),g(t)为实系数式项式,且h(t)=g(t)-tf(t),如果f(0),g(0)>0,Zf和Zg非空,且min(Zg) 引理5 当n≥3,2≤r 证明:(以下证明采用引理3的记号) 假定αi=0(i=1,…,n),可得a1=a2=…=ar-1=1,而aj(j=r,r+1,…,n-2,n)是关于b的多项式. 令j=r,r+1,…,n-2,上述多项式满足aj(b)=aj-1(b)-baj-r(b).令h(b)=an-2(b)-ban-r-1(b).容易验证aj(0)=1(j=r,r+1,…,n-2),且h(0)=1.令ar+i(b)=1-(i+1)b=0(i=0,1,…,r-1),可得b=.因此min(Za) 由上式可知min(Za2r-1) 同理,反复用引理3可知min(Zh) ar+i(b)=1-(i+1)b,(i=0,1,…,n-r-2) 0=an-2(b)-ban-r-1(b), an(b)=ban-r(b). 与前同理,可得min(Zh) 引理6[4]一个n阶不可约谱任意符号模式至少有2n-1个非零元. 定理1 当n≥3,2≤r 证明:由引理1,引理3和引理5得证. 定理2 当n≥3,2≤r 证明:当n≥3,2≤r (1)sn-1,n-1≠0,否则S的迹为正,与S是SAP矛盾. (2)si,i+1≠0.(i=2,…,n-r-1,n-r+1,…,n),否则S是符号奇异的,与S是SAP矛盾. (3)sn-r,n-r+1≠0.sn,n-r+1≠0,否则S是符号非奇异的,与S是SAP矛盾. (4)si,1≠0(i=1,2,…,n-2,n),否则由引理3(1)知αi≠0,与S是SAP矛盾. 再由引理6可知,An,r的任意真子模式都不是谱任意的,即An,r是MSAP,定理得证. [1] DREW J H,JOHNSON C R,OL ESKY D D,et al.Spectrally Arbitrary Patterns[J].Linear A lgebra A pplication,2000, 308:121-137. [2] MCDONALD J J,OL EXKY D D,TSATSOMEROS M J,et al.On the Spectra of Striped Sign Patterns[J].Linear Multilinear A lgebra,2003,51:39-48. [3] CAVERS M S,KIMI J,SHADER B L,et al.On Determining Minimal Spectrally Arbitrary Patterns[J].Elec J L inear A lgebra,2005,13:240-248. [4] BRITZ T,MCDONALD J J,OLESKY D D,et al.Minimal Spectrally Arbitary Sign Patterns[J].S IA M J Matrix A nal A ppl,2004,26:257-271. [5] GAO Yu-bin,SHAO Yan-ling.A Spectrally Arbitrary Pattern[J].A dvances in Mathematics,2006,35:551-555. [6] GAO Yu-bin,SHAO Yan-ling,LI Zhong-shan.A Note on Spectrally Arbitrary Sign Patterns[J].J P Journal of A lgebra, N umber Theory and A pplications,2006,11:15-35. [7] MCDONALD J J,STUART J.Spectrally Arbitrary Ray Patterns[J].Linear A lgebra and Its A pplications,2008,429: 727-734. [8] LI Shou-cang,GAO Yu-bin.Two New Classes of Spectrally Arbitrary Sign Patterns[J].A rs Combinatoria,2009,90:209-220. [9] CAVERS M S,VANDER MEUL EN K N.Spectrally and Inertially Arbitrary Sign Patterns[J].Linear A lgebra A ppl, 2005,394:53-72. A Class of Minimal Spectrally Arbitrary Patterns with 2nNonzero Entries WANG Yan-ling,SHAO Yan-ling Ann×nsign patternAis a spectrally arbitrary pattern.If for any given real monic polynomial f(x)of degreen,there is a real matrixB∈Q(A)so that it charateristic polynomial isf(x).andAis known as a spectrally arbitrary pattern.IfAis a spectrally arbitrary pattern and no proper subpattern ofA is spectrally arbitrary,thenAis a minimally spectrally arbitrary pattern.In this paper,we introduce a class of minimally spectrally arbitrary patterns with 2nnonzero entries for ordern≥3. sign pattern matrix;nilpotent matrix;spectrally arbitrary pattern O157 A 0253-2395(2010)03-0349-05 2009-05-06; 2010-02-16 国家自然科学基金(10571163);山西省自然科学基金(2007011017,20090110007) 王燕玲(1981-),女,硕士研究生,研究方向:组合数学.E-mail:fromwangyanling@163.com1 有关结论

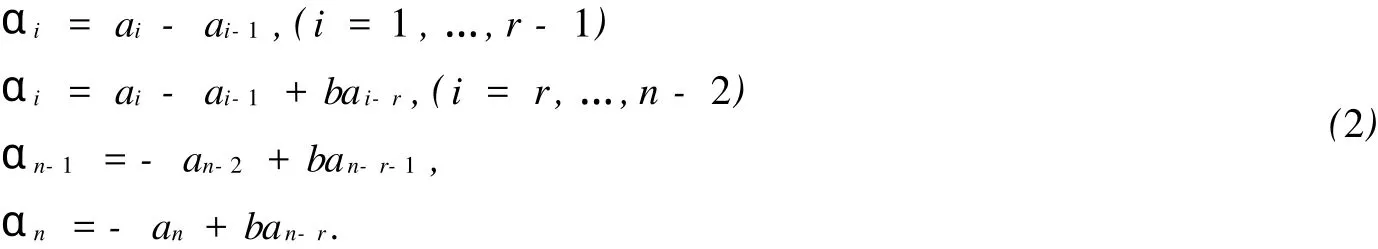

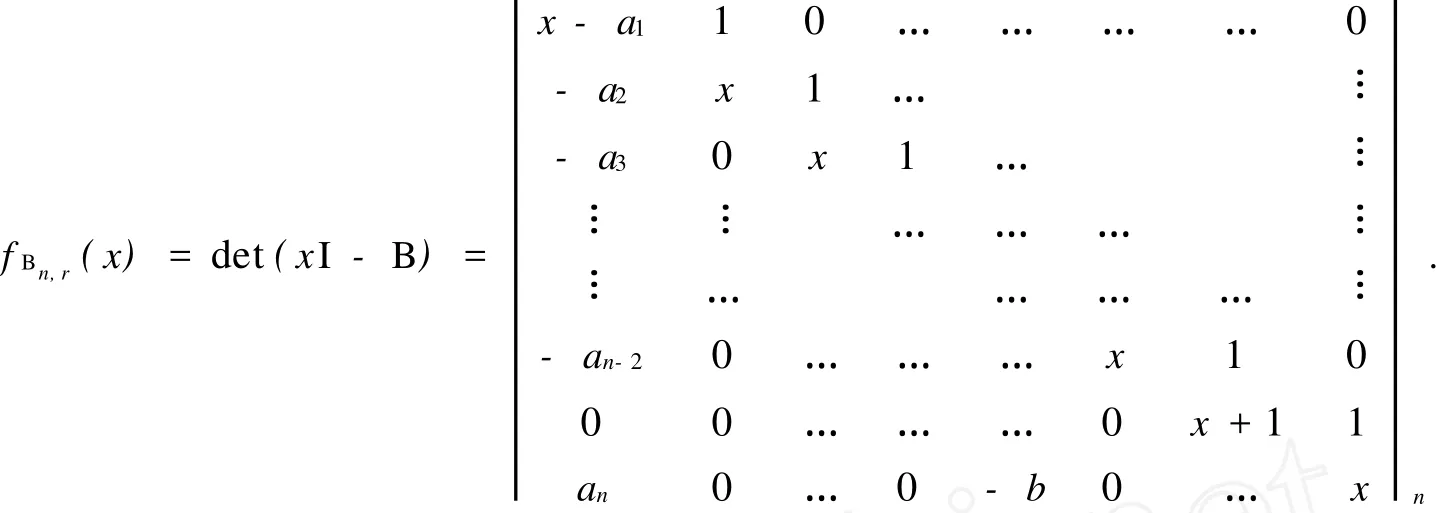
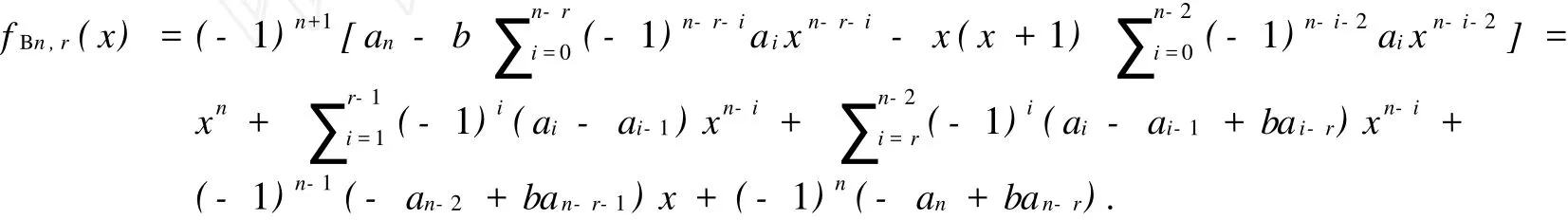


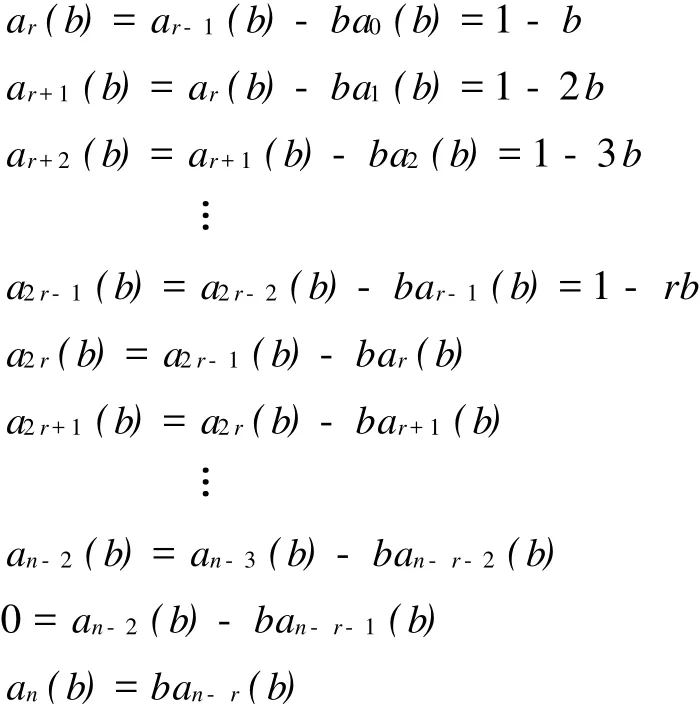
2 主要结果
(Department of Mathematics,North University of China,Taiyuan030051,China)

