零成分搜索法的模拟分析

马海南,张应山

零成分搜索法的模拟分析

马海南1,张应山2

(1.浙江工业职业技术学院人文社科部,浙江绍兴312000; 2.华东师范大学统计与精算学系,上海200241)

主要考察了零成分搜索法的模拟分析.首先简述了零成分搜索法的计算步骤,其次用一个模拟例子阐述了零成分搜索法的应用过程;最后模拟计算了零成分搜索法进行列显著性判断时所犯两类错误概率的大小.模拟分析结果表明,零成分搜索法不仅可以较好地识别不显著列,而且对误差方差的估计也有不错的结果.

正交表;矩阵像;饱和模型;子成分;零成分搜索

0 引言

针对饱和正交表模型,文[1]提出了非中心F统计量[2]和零效应搜索[3]两种方法,鉴于零效应搜索法在两水平饱和正交表上的成功应用,我们将该思想推广到任意水平以及混合水平,提出了零成分搜索法[4].虽然文[4]中已经证明,零成分搜索法中使用的W统计量具有一些比较好的性质,但是其在识别零成分时是否真如我们预料的那么有效,仍然需要我们做进一步研究.本文通过模拟分析表明,零成分搜索法不仅可以较好地识别不显著列,而且对误差方差的估计也有不错的结果.

全文主要由三部分构成.第一部分简述了零成分搜索法的计算步骤;第二部分模拟零成分搜索法的实际应用过程;第三部分考察零成分搜索法在列显著性判时所犯两类错误概率的大小.

1 零成分搜索法

假设饱和正交表Ln(v1,…,vm)和列对应的矩阵像依次为A1,…,Am,总均值列所对应的矩阵像为A0(矩阵像的定义可参看文[5-7]).由矩阵像的定义,如下分解式成立:这里简述零成分搜索法的计算步骤:

1、进行成分分解,得到子成分及子矩阵阵像,求出子平方和,得到如下分解式:

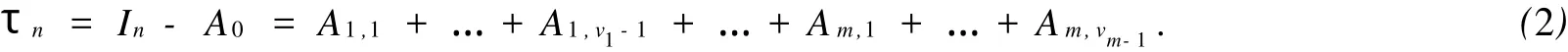
计算平方和SSj,x=YTAj,xY,x=1,…,(vj-1),j=1,…,m,并且有

2、对这n-1个部分平方和进行排序,得到n-1个次序统计量ξ1,…,ξn-1,利用这些次序统计量构造W统计量:

从W2,…,Wn-1中找出第一个比相应W统计量临界值(由模拟分布确定)大的那个,之前的那些次序统计量对应的子成分都可以看做是零成分,其余都是非零成分.

3、不妨假设前u个次序统计量相应的子成分为零成分,误差方差的估计公式为:

对其他的非零成分θv(对应的次序统计量为ξv)考虑假设检验问题:

构造F统计量:

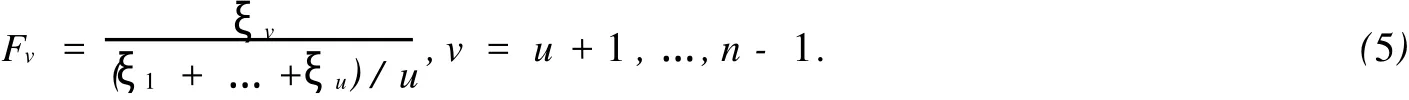
在原假设条件下Fv服从F(1,u)分布.

4、参数向量的最小二乘无偏估计值:^Θt=AtY,t=0,1,…,m.

2 模拟分析

取饱和正交表其相应统计分析模型

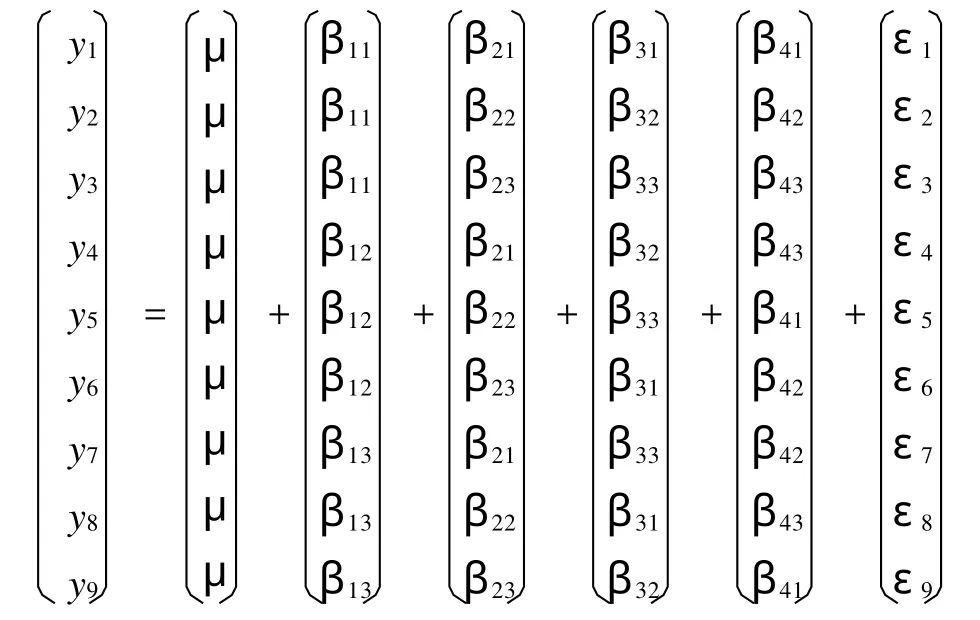
不妨简记为:

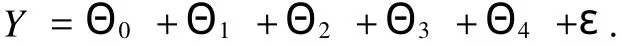
约束条件:β11+β12+β13=0,β21+β22+β23=0,β31+β32+β33=0,β41+β42+β43=0.另外记β1=(β11,β12,β13)T, β2=(β21,β22,β23)T,β3=(β31,β32,β33)T,β4=(β41,β42,β43)T.

先随机取定参数(由约束条件每个列向量中都有一个参数是由其他参数所决定的),再产生9个随机数εi～N(0,σ2),这里需要注意控制所取参数的大小.如果要使得该参数为显著,则其绝对值应该大于3σ;如果该参数不显著,则可以取该参数值比较小或为零.由上述模型,就可以得到9个观测值,再根据9个观测值,可以对参数进行估计并且做方差分析.

下面通过一个具体的模拟例子来看看零成分搜索法的应用过程,先给定各个主效应参数的值(P377表4),再产生9个随机数(P377表1),这样得到9个观测值(P377表1),有了这9个观测值,就可以按照零成分搜索法的数据分析步骤进行计算,得到以下结果(表2,表3,表4).

表1 随机数及测值(σ2=4)Table 1 Random Numbers and Observations(σ2=4)

表2 零成分搜索表Table 2 The Table of Searching Zero-Decompositon

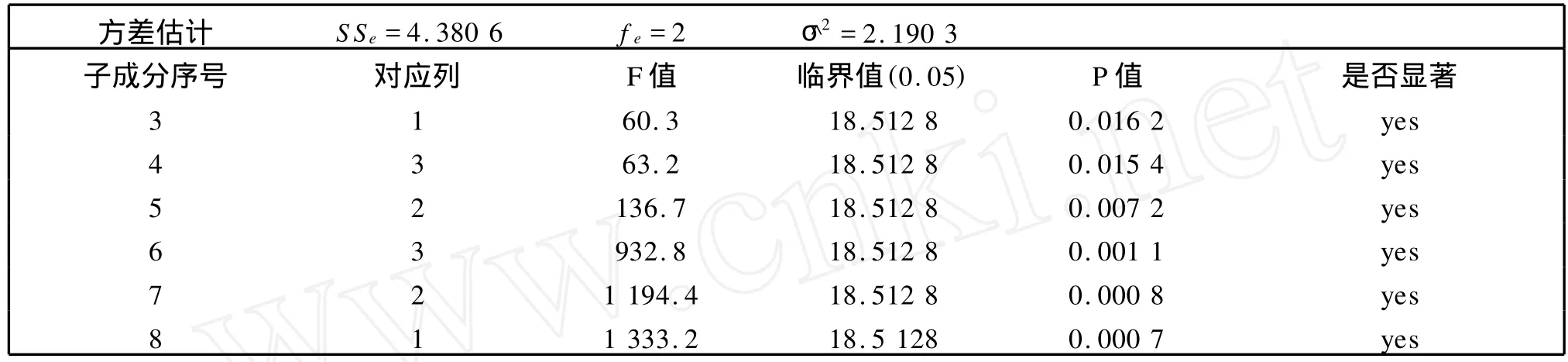
表3 非零子成分方差分析表Table 3 The Table of Variance Analysis to Non-Zero-Decompostion

表4 效应参数估计及显著性判断Table 4 Estimation of Main Effect Parameters and Judgement of Column Significant

结果分析:正交表第四列的效应值被人为设置为0,表2的零成分搜索结果也正好将该列对应的两个子成分都识别为零成分,这表明零成分搜索法的确能够识别出零成分;表3中的误差方差的估计在0.5倍左右,这个结果在饱和情形已经算是相当不错的结果;表4中对各列效应参数的估计也是比较令人满意的,估计误差基本在σ的一倍左右.

3 列显著性判断两类错误概率的模拟计算

上节对零成分搜索法进行了模拟分析,然而仅仅模拟一次具有很大的偶然性,本节应用模拟的办法来计算零成分搜索法进行列显著性判断时犯两类错误的概率.

对饱和正交表列效应的显著与否,用统计量进行判断,必然导致两类错误的产生,这两类错误分别是:将不显著列误判为显著(第一类错误);将显著列误判为不显著(第二类错误),对我们的问题来讲,第二类错误应该尽量减少.

应用模拟的办法来计算这两类错误发生的概率,具体做法如下:选取一张饱和正交表,对该表的所有列都安排因子,但是每列对应的因子是否显著则用随机的方法给出.如果该列被指定为显著,则正效应取一个大于σ的随机值(负效应由这些约束条件决定),如果该列被指定为不显著,则所有效应取为比较小或零.然后产生随机数,得到观测数据,对这些以观测数据进行统计分析,得到一个关于各列显著性判断的结果.将这个结果与真实结果进行比较,得到是否误判的结论.

进行一定次数的模拟,统计模拟过程中随机得到某列是显著或不显著的次数,并统计该列显著时被误判为不显著的次数以及该列不显著时被误判为显著的次数.利用后面的次数除以前面对应的次数,就分别得到第一和第二类错误的概率.此外,还可以计算列显著性判断时误判次数的一个统计数字.

仍然以饱和正交表L9(34)为例,进行模拟.

模拟一:考虑显著性列正效应在(3σ,8σ)随机取值(见表5).

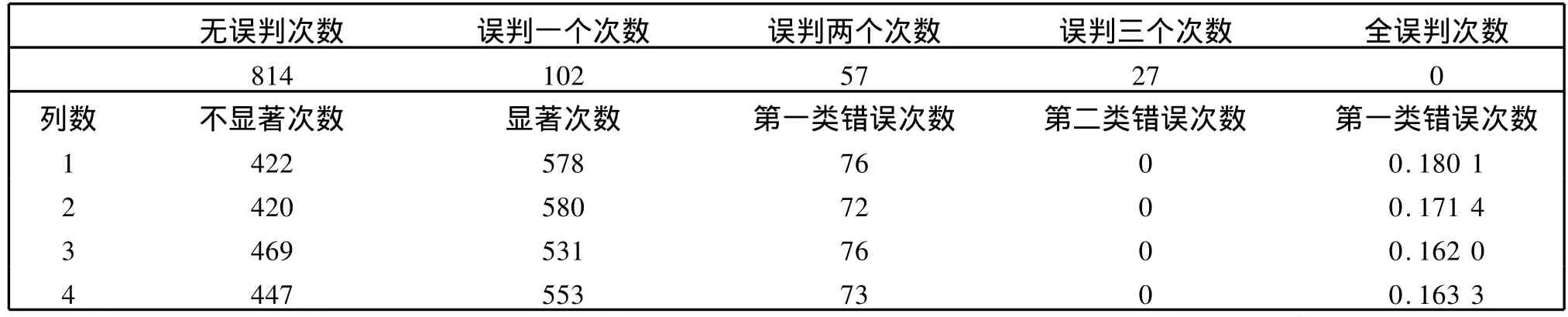
表5 正效应在(3σ,8σ)随机取值时一千次模拟误判次数与两类错误概率Table 5 Counts of errors and probability of two types of errors to 1 000 times simulation when positive effects are random numbers in(3σ,8σ)

模拟二:考虑显著性列正效应在(2σ,4σ)随机取值(见表6).

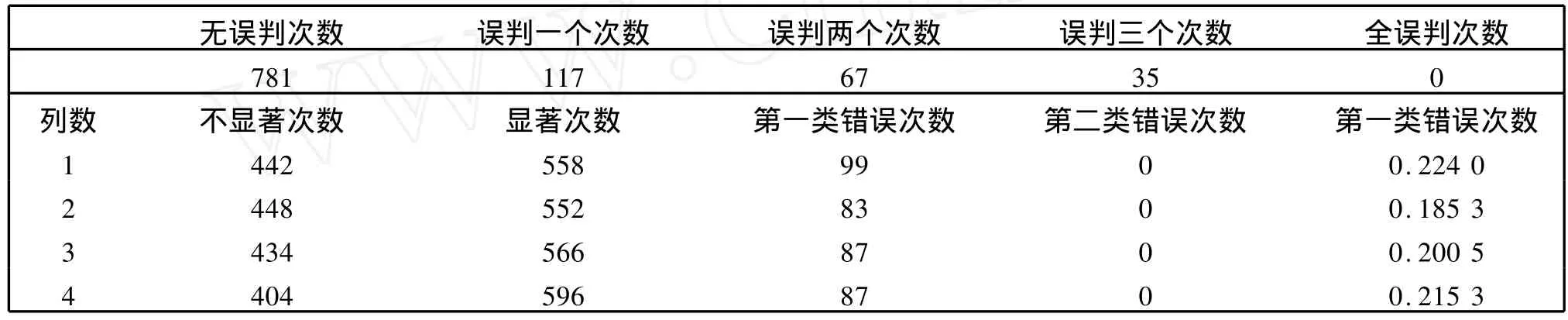
表6 正效应(2σ,4σ)随机取值时一千次模拟误判次数与两类错误概率Table 6 Counts of errors and probability of two types of errors to 1 000 times simulation when positive effects are random numbers in(2σ,4σ)

模拟三:考虑显著性列正效应在(σ,3σ)随机取值(见表7).

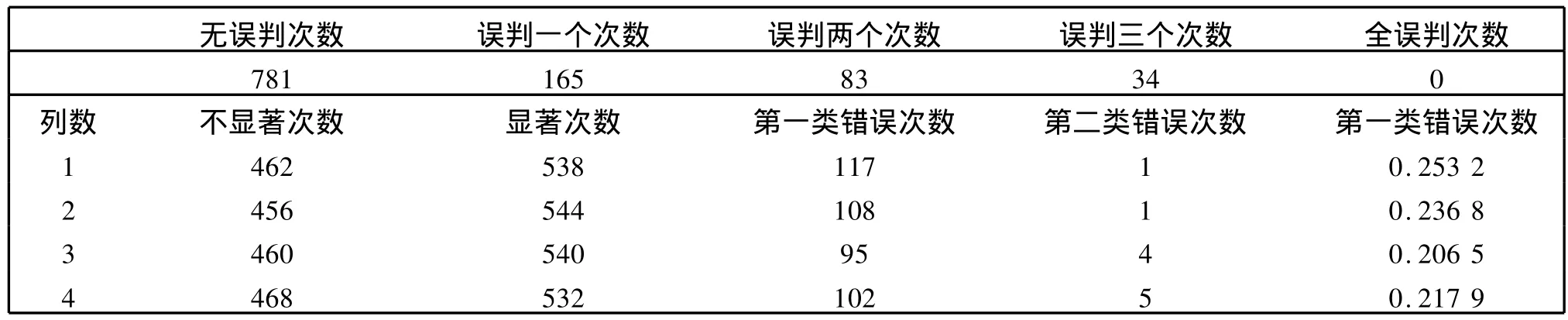
表7 正效应(σ,3σ)随机取值时一千次模拟误判次数与两类错误概率Table 7 Counts of Errors and Probability of Two Types of Errors to 1000 Times Simulation when positive effects are random numbers in(σ,3σ)

从误判次数的统计数据情况来看,零成分搜索法全误判次数为0,无误判次数所占比重可以达到70%以上,误判两个以上的次数比较小,误判一个的次数相对较多,不过仍然在可以接受的范围之内.

从两类错误概率的模拟计算数据我们可以发现,随着显著效应取值逐渐靠近误差方差,犯两类错误的概率也在逐渐变大.另外该方法犯第二类错误的概率比较小,而犯第一类错误的概率比较大,这与本问题的要求一致,即宁可接受将一个不显著的列判为显著列,也不能忍受将一个显著列误判为不显著列.当然如果使得犯两类错误的概率都比较小,最好的办法就是增加试验次数.

[1] 张晓琴.正交饱和效应模型的统计分析[D].上海:华东师范大学,2007.

[2] 张晓琴.正交饱和设计的统计分析[J].应用概率统计,2007,23(1):91-101.

[3] 张晓琴.二水平正交饱和设计的统计分析-零效应搜索法[J].华东师范大学学报(自然科学版),2007,24(1):51-59.

[4] 潘长缘,陈雪平,张应山.正交表列效应的约束条件检验[J].山西大学学报(自然科学版),2008,31(3):380-384.

[5] 张应山.多边矩阵理论[M].北京:中国统计出版社,1993.

[6] 张应山.正交表的数据分析及其的构造[D].上海:华东师范大学,2005.

[7] ZHANG Y S,LU Y Q,PANG S Q.Orthogonal Arrays Obtained by Orthogonal Decomposition of Projection Matrices[J]. Statistica Sinica,1999,9:595-604.

Simulation Analysis of Searching Zero-Decomposition

MA Hai-nan1,ZHANG Ying-shan2
(1.Department ofHumanities and Social Sciences,Zhejiang Industry Polytechnic College,Shaoxing312000,China; 2.Department of Statistics and Actuarial Science,East China Normal University,Shanghai200241,China)

The simulation analysis of Searching Zero-Decompostion was studied.Firstly,the step of Searching Zero-Decompostion was listed.Secondly an example to simulate the procedure of Searching Zero-Decompostion was specified.Thirdly the probability of two types of errors was also calculated when judging a colume is significant or not.The results simulation analysis illustrated that Searching Zero-Decompostion not only distinguishs the non-signficant column from unknown column successfully,but also estimates the variance of errors well.

orthogonal arrays;matrix images;saturated model;decompositon;searching Zero-Decompostion

O212.6

A

0253-2395(2010)03-0375-05

2009-10-22

国家自然科学基金(10571045);国家自然科学基金(44k55050);高校博士点专项基金

马海南(1978-),浙江嵊州人,在职硕士,讲师,主要从事概率统计方面的研究.E-mail:mhn78@sina.com